|
|
On étudie un oscillateur
électrique idéal représenté figure ci-dessous :
Il est constitué par :
· un condensateur de capacité C = 0,50 μF
· une bobine d'inductance L = 0,50 H.
· La résistance du circuit est négligeable.
On charge le condensateur, la tension à ses bornes vaut : UAB(t=
0) = U0 = 5,0 V.
Puis à t = 0, on ferme l'interrupteur K.
Soit q la charge de l'armature A du condensateur à un instant t
quelconque (t > 0).
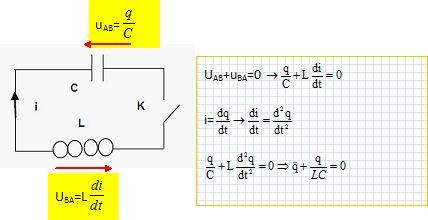
Ecrire
l'expression de la tension aux bornes du condensateur en fonction de q
et de C.
Écrire
l'expression de la tension aux bornes de la bobine en fonction de q, L
et t.
Déduire
l'équation différentielle qui régit les variations de la charge q.
L'équation différentielle admet une solution de la forme : q = Qm
cos (ω0t + f).
Que
représentent les grandeurs Qm et ω0 ? Déterminer les
valeurs numériques correspondantes.
Qm
: charge initiale du condensateur soit CU0 = 5,0 10-7*5
=2,5 10-6 C.
ω0
= 1/(LC)½, pulsation :1/(0,5*5,0 10-7)½=2,0 103 rad/s.
Le symbole f
représente la phase à l'origine.Vérifier que la
valeur f = 0 est en accord
avec les conditions de l'étude.
q (t=0) = Qm
cos ( f) = CU0
=2,5 10-6 Coulomb.
La valeur f = 0 est en accord avec les conditions de l'étude.
Calculer la période propre T0 des
oscillations.
T0
= 2 p / ω0= 3,14 10-3 s.
|
| .
. |
.
L'oscillateur réel.
On réalise l'étude
expérimentale
d'un oscillateur électrique constitué par un condensateur de capacité C
= 0,50 μF et une bobine d'inductance L = 0,50 H. Soit R la résistance
totale du circuit.
A l'aide d'une carte d'acquisition reliée à un ordinateur et d'un
logiciel de traitement des données, on obtient le document ci-après
représentant :
- d'une part, les variations de la charge q du condensateur en fonction
du temps t : ordonnée (q) (axe gradué à gauche) ;
- d'autre part les variations de l'énergie Emag emmagasinée
dans la bobine en fonction du temps t : ordonnée Emag (axe
gradué à droite).
Dans la suite, on notera Eel l'énergie emmagasinée dans le
condensateur.
Déterminer
graphiquement la valeur de la pseudo-période T des oscillations.
Déduire
du graphique la valeur de la tension aux bornes du condensateur à la
date t = 0.
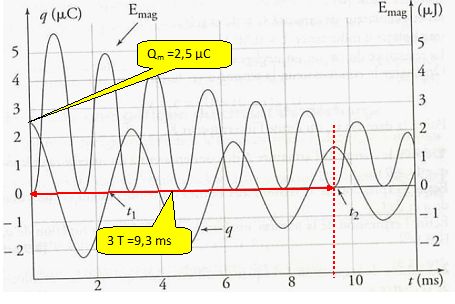
T = 9,3 /3 = 3,1
ms ; U0 = Qm/C = 2,5 10-6 / 5 10-7
=5,0 V.
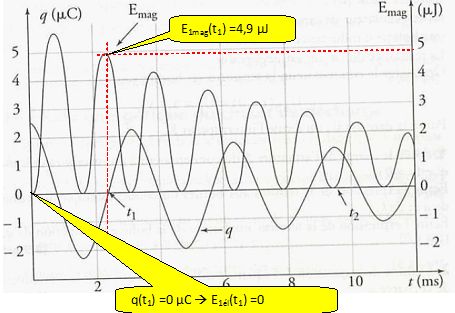
Pour
l'instant t1 = 2,4 ms, déterminer à partir du graphique :
la
valeur de l'énergie E1mag emmagasinée dans la
bobine ; la valeur de l'énergie E1el emmagasinée dans le
condensateur ; la valeur de l'énergie électromagnétique E1 du circuit.
E1 = E1mag +E1el
= 4,9 µJ.
Pour l'instant t2 = 9,5 ms, déterminer à partir du graphique
:
la
valeur de l'énergie E2mag emmagasinée dans la
bobine ; la valeur de l'énergie E2e1 emmagasinée dans le
condensateur ; la valeur de l'énergie électromagnétique E2 du circuit.
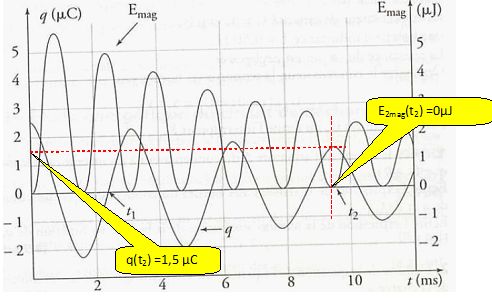
E2e1 = ½q2/C
= 0,5 *(1,5 10-6)2 / 5,0 10-7 =2,25 10-6
J~2,3 µJ. E2
= E2mag +E2el
= 2,3 µJ.
A partir du graphe,
justifier la conservation ou la non-conservation de l'énergie
électromagnétique du circuit. Quel phénomène physique explique ces
résultats ?
L'énergie totale du dipole (LC) diminue avec le temps : non
conservation de l'énergie. Lors des échanges d'énergie entre
condensateur et bobine, une partie de l'énergie est dissipée par effet
Joule dans les parties résisrives du circuit.
On admettra la relation E2/ E1
= exp(-R/L(t2-t1)) (relation valable pour les
amortissements faibles). Déterminer une
valeur approchée de la résistance R du circuit.
ln(E2/ E1) =-R/L(t2-t1)
; R = ln(E1/ E2) L /(t2-t1)= ln(4,9/2,3)*0,50
/ (9,5-2,4)10-3 ~ 53 ohms.
|
|



