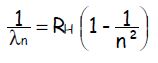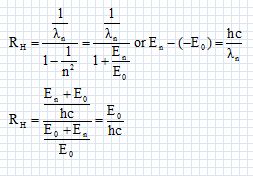«
Les galaxies comme la nôtre, la Voie Lactée, ont un éclat bien trop
faible pour être étudiées en détail dès qu’elles sont à des distances
de quelques millions d’années lumière.
Mais heureusement certaines galaxies abritent en leur centre un noyau
anormalement lumineux : un quasar. Le spectre d’un quasar contient des
raies d’émission, associées au quasar lui-même, et des raies
d’absorption. A partir de la raie d’absorption « Lyman alpha » de
l’atome d’hydrogène, à 121,5 nanomètres de longueur d’onde, on détecte
aisément des nuages intergalactiques cent mille fois moins denses que
la paroi d’une bulle de savon. »
Extrait d’un texte de revue scientifique.
|
|
Données :
Constante de Planck : h = 6,62 x 10-34 J.s ; célérité de la
lumière : c = 3,00 x 108 m.s-1 ;
1 eV = 1,60 x 10-19 J ; niveaux d’énergie de l’atome
d’hydrogène : En = -E0 / n2 avec E0 = +13,6 eV.
Préciser
l’intérêt présenté par les quasars pour les études des astrophysiciens,
par rapport aux autres objets stellaires.
Un quasar est situé au centre d'une
galaxie et est très lumineux : l'éclat de ce type de galaxie lointaine
est important, son observation depuis la terre sera donc possible.
Dans quel domaine de
radiation est située la raie « Lyman alpha ».
121,5 nm, valeur inférieure à 400 nm, appartient au proche UV.
Diagramme énergétique de
l’hydrogène.
Dans
l’expression des niveaux d’énergie En, préciser les
valeurs que peut prendre le paramètre n.
n est un nombre entier positif supérieur ou égal à 1.
En
déduire l’énergie du niveau fondamental.
n=1 : E1
= -13,6 eV
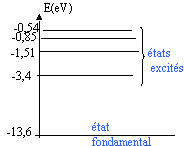
Construire le
diagramme énergétique de l’atome d’hydrogène en calculant et en plaçant
les trois premiers niveaux.
n=1 : E1 = -13,6 eV ; n=2 : E2 = -13,6 / 4 = -3,4
eV ; n=3 : E3 =-13,6 / 9 = -1,51 eV.
|
| .
. |
.
.
Série de raies d'absorption.
La raie d’absorption « Lyman alpha » fait partie de la série dite de Lyman dans laquelle les
absorptions se font du niveau fondamental vers les niveaux excités de l’atome. Les
longueurs d’onde des raies d’absorption sont données par la relation 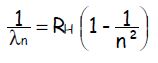
où RH est la constante de Rydberg.
Montrer que RH est donnée par l’expression RH = E0 / (hc).
Calculer sa valeur.
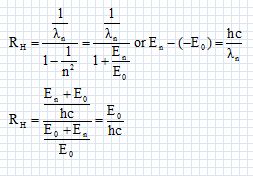
RH =13,6 *1,6 10-19 /(6,62 10-34*3,00 108)=1,0957 107~1,1 107 m-1.
Calculer la plus petite et la plus grande des longueurs d’onde de la série de Lyman.
Transition du niveau fondamental au premier niveau excité : l1 = hc/ (E1-(-E0)) =6,62 10-34*3,00 108) / (-3,4+13,6) *1,6 10-19) =1,22 10-7 m = 121 nm.
A quelle transition correspond la raie « Lyman alpha » ?
Transition du niveau fondamental au premier niveau excité.
Quelle est en eV l’énergie du photon absorbé ?
E1-(-E0) = -3,4+13,6 = 10,2 eV.
|
|