Grâce
aux sondes Voyager (1977-1989), nous connaissons actuellement
l'existence de 15 satellites de la planète Uranus. Les 5 plus gros
d'entre eux ont été découverts bien avant, grâce aux observations
depuis la Terre, entre 1787 et 1948. L'observation de ces 5 satellites
a permis de déterminer les caractéristiques suivantes :
Nom
|
Diamètre
( km)
|
Rayon
moyen de l'orbite r ( 106 m)
|
Période
de révolution T (j)
|
Année
de découverte
|
Titania
|
1578
|
435,8
|
8,71
|
1787
|
Obéron
|
1523
|
582,6
|
13,50
|
1787
|
Umbriel
|
1169
|
266,0
|
4,14
|
1851
|
Ariel
|
1158
|
191,2
|
2,52
|
1851
|
Mirnada
|
472
|
129,8
|
1,41
|
1948
|
|
|
Constante de
gravitation universelle : G = 6,67 x 10-11 S.I. ; 1 jour =
86 400 s .
On supposera que la répartition de masse d'Uranus et de ses satellites
est à symétrie sphérique.
D'autre part, les caractéristiques de ces satellites sont données par
rapport au référentiel A,supposé galiléen, défini par le centre
d'Uranus et trois étoiles très éloignées.
On admet que le mouvement des centres des satellites
est circulaire uniforme dans le référentiel A.
Établir
l'expression littérale de la vitesse de révolution v du centre d'un
satellite en fonction du rayon r de sa trajectoire et de sa période T
de révolution.
Le satellite décrit la circonfrence 2pr,
exprimée en mètre, à la vitesse v, exprimée en m/s, en T seconde.
v = 2pr / T.
Calculer
la vitesse de révolution du centre d'Umbriel dans le référentiel A en
m.s-1.
T = 4,14 j = 4,14 *86400 =3,57696 105 s.
v = 2*3,14*266 106 / 3,57696 105= 4,6725 103
~4,67 103 m/s.
Relation entre la
vitesse de révolution et le rayon de l'orbite.
En
utilisant les données du tableau ci-dessous et le résultat précédent
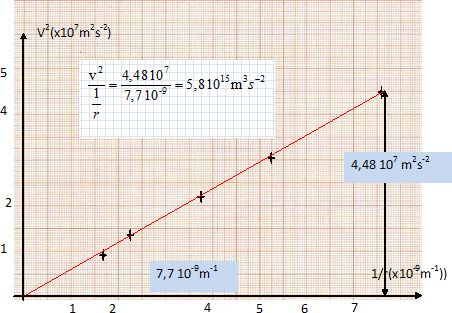
obtenu pour Umbriel, tracer la représentation graphique de la fonction v2
= f (1 / r).
|
Titania
|
Obéron
|
Umbriel
|
Ariel
|
Miranda |
1/r
(x10-9 m-1)
|
2,29
|
1,72
|
3,76
|
5,23
|
7,70
|
v2(x107
m2s-2)
|
1,32
|
0,98
|
2,18
|
3,04
|
4,48
|
| v2
r
(x1015 m3s-2) |
5,76
|
5,70
|
5,80
|
5,81
|
5,82
|
En déduire la
relation entre v2 et 1/r.
v2 ~ 5,8 1015 / r.
|
.
.
|
.
.
Calcul de la masse d'Uranus.
Démontrer que le
mouvement circulaire du centre d'un satellite d'Uranus est
nécessairement uniforme.
Un satellite est soumis uniquement à la force attractive centripète
d'Uranus. Cette force est constamment perpendiculaire à la vitesse du
satellite.
Une force perpendiculaire à la vitesse, ne travaille pas et l'énergie
cinétique du satellite reste constante. La valeur de la vitesse est
constante : le mouvement est uniforme.
Établir
l'expression de v2 en fonction de G, r
et de la masse M d'Uranus.
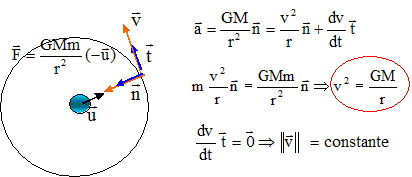
Montrer que
l'expression obtenue pour v2 est en accord avec
la représentation graphique.
v2 est proportionnelle à 1/r : le graphe v2 =
f(1/r) est une droite passant par l'origine et de pente égale à GM.
Déduire
de cette représentation la masse d'Uranus.
M = 5,8
1015 / 6,67 10-11 =8,7
1025 kg.
|
|