.
|
|
Phénomène de réflexion totale.
On
considère un rayon lumineux, issu d'une radiation monochromatique,
arrivant sur une interface plane séoarant deux milieux d'indices n1 et
n2 sous un angle d'incidence i.
Enoncer la loi de Snell-Descartes.
Lois de Descartes relatives à la réflexion
et à la réfraction de la
lumière :
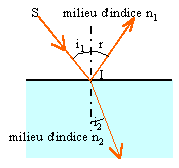
Les trois rayons incident, réfléchi et
réfracté sont dans le même plan ;
l'angle d'incidence i1 est égal à
l'angle de réflexion r. Les angles d'incidence
i1 et réfracté i2 sont
reliés par la relation : n1 sin
i1 = n2 sin
i2.
Décrire le phénomène de réflexion totale. Calculer l'angle limite.
Lors du passage de la lumière d'un milieu d'indice n1 à un milieu d'indice n2 < n1, il existe un angle d'incidence limite ilim au dela duquel le rayon réfracté n'existe plus : seul le rayon réfléchi existe.
n1 sin
i1 = n2 sin i2 et
|sin i2| inférieur ou égal à
1.
n1 sin
ilim = n2 soit sin ilim = n2 /
n1.
Condition d'acceptance d'une fibre optique.
Une fibre optique à saut d'indice est constituée d'un coeur cylindrique d'indice nc et d'une gaine cylindrique d'indice ng entourant le coeur avec ng < nc. Un rayon situé dans le plan Oxy entre dans la fibre au point O avec un angle d'incidence q. 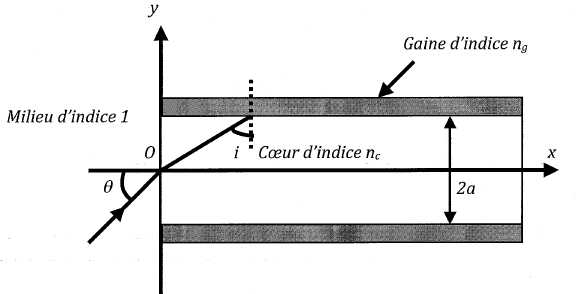
A quelle condition sur i, angle d'incidence à l'interface coeur-gaine, le rayon reste-t-il confiné à l'intérieur du coeur ?
sin ilim = ng /
nc ; i doit être inférieur à ilim.
Montrer que la condition précédente induit une valeur limite qlim de q.
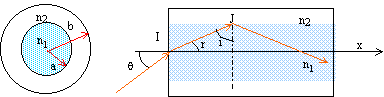 en I, dioptre air/coeur :
nair sin qi
= nc sin r ; sin qi
= nc sin r
(1).
en J, il y a réflexion
totale : sin ilim = ng /
nc ; les angles i et r sont
complémentaires soit sin r = cos i.
(1) donne : cos i = sin q / nc ; sin q = nc cos i ; sin qlim = nc cos ilim ;
q doit donc être inférieur à qlim.
Un
raisonnement identique peut être fait pour tous les plans Oxy, quelle
que soit leur inclinaison par rapport au plan vertical. On dit qu'il
existe un cône d'acceptance associé à la fibre permettant au rayon de
se propager par réflexions totales dans la fibre.
|
| .
. |
.
.
Propagation dans la fibre optique.
On
considère une fibre optique de longueur L. Le rayon entrant dans la
fibre respecte la condition établie dans la partie précédente.
Exprimer
la vitesse de propagation de la lumière dans le coeur de la fibre.
v = c / nc avec c = 3,00 108 m/s.
On considère le rayon tel que q=0.
Calculer la durée de parcours t1 de ce rayon dans la fibre de longueur L.
t1 = L / v = L nc / c.
On considère le rayon tel que q = qlim.
Calculer la durée de parcours t2 de ce rayon dans la fibre de longueur L.
Expression de la distance d
parcourue par la lumière en fonction de son angle
d'incidence qi
et de la longueur de la fibre L :
Figure ci-dessus, expression de IJ
: ( on note h la projection de IJ sur l'axe de la
fibre).
cos r = h / IJ; or sin
qi
= nc sin r ; cos² r + sin² r = 1
;
h² / IJ² +( sin
qi
/ nc )² = 1 ; h / IJ = [1-( sin
qi
/ nc )²
]½.
Le rapport entre la longueur L de
la fibre et le trajet d suivi par la lumière est :
L/d =[1-( sin qi
/ nc )²
]½
d = L[1-( sin
qi
/ nc )²
]-½ soit pour l'angle qlim : d = L[1-( sin
qlim
/ nc )²
]-½ .
t2 = d / v = d nc / c.
En déduire Dt = t2-t1.
Dt = nc L / c ( [1-( sin
qlim
/ nc )²
]-½ -1).
A.N : nc = 1,50 ; ng = 1,47 ; L = 1 km.
sin ilim = ng /
nc =1,47 / 1,50 = 0,98 ; ilim = 78,52.
sin qlim = nc cos ilim = 1,50 *cos 78,52 = 0,2985.
Dt = 1,5 *103 / (3 108) ( [1-( 0,2985
/ 1,5 )²
]-½ -1) = 1,02 10-7 ~1 x 10-7s.
Quelle
durée T doit séparer deux impulsions successives pour qu'elles ne se
superposent pas à la sortie de la fibre ? En déduire une valeur limite
D pour le débit de la fibre optique.
On souhaite transmettre une
suite de 0 ( la source lumineuse envoie un très bref
éclair puis attend une durée T =Dt ) et de 1 ( pas
de lumière pendant la même durée ), la
fréquence maximale de transmission d'une ligne de
longueur 1 km est : il ne faut pas que deux signaux
consécutifs se superposent à la sortie
d'où la fréquence maxi : 1/ (1,02 10-7)
= 9,8 106 ~ 1 x 107 Hz.
|
|
|


