Moteur de Stirling : concours ITPE 2012. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. Le moteur de Stirling constitue un système fermé : le gaz est confiné dans le moteur et aucune combustion n'a lieu à l'intérieur du moteur. On modélise le gaz par un gaz parfait. Sa quantité de matière est notée n. On note R= 8,31 J mol-1 K-1 la constante des gaz parfaits, Cvm= 21 J mol-1 K-1 la capacité thermique à volume constant. 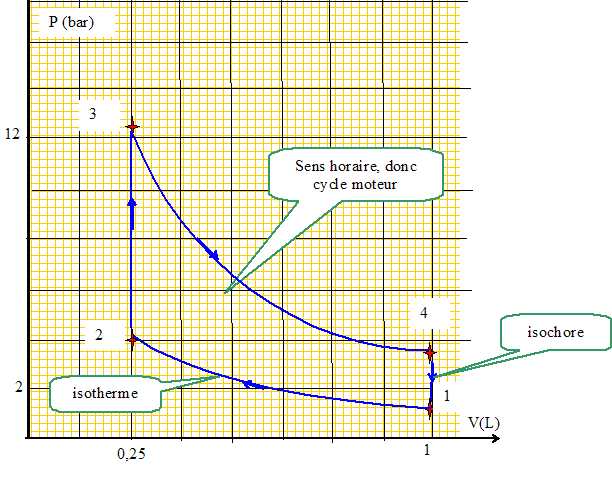Le fonctionnement du moteur est modélisé par un cycle constitué de 4 transformations supposées réversibles : 1--> 2 : compression isotherme à la température Tf de la source froide. Le volume évolue de V1 à V2. 2 --> 3 : échange thermique isochore jusqu'à la température Tc. 3 --> 4 : détente isotherme à la température Tc jusqu'au volume initial. 4 --> 1 : échange thermique isochore jusqu'à la température Tf. Tracer l'allure du cycle dans le diagramme (PV). Compléter le tableau ci-dessous en explicitant les calculs. état 1 état 2 état 3 état 4 T(K) 300 300 930 930 V (m3) 1,00 10-3 2,5,0 10-4 2,50 10-4 1,00 10-3 P(Pa) 1,00 105 4,00 105 1,24 106 3,10 105 Compression isotherme 1-->2 ; détente isotherme 3-->4. Chaufage isochore 2-->3 ; refroidissement isochore 4 --> 1. n = P1 V1 / (RT1) = 1,00 105*1,00 10-3 /(8,31*300) =4,0112 10-2 mol. P2 = nRT2/ V2 =4,0112 10-2 *8,31 *300 / (2,5,0 10-4 ) =4,00 105 Pa. P3 = nRT3/ V3 =4,0112 10-2 *8,31 *930 / (2,5,0 10-4 ) =1,24 106 Pa. P4 = nRT4/ V4 =4,0112 10-2 *8,31 *930 / (1,0 10-3 )=3,10 105 Pa. . . . . Exprimer et calculer les travaux sur chacune des transformations. Les travaux sont nul au cours des transformations isochores. W23 = W41 =0. 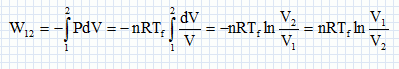Au cours d'une transformation isotherme : W12 = 4,0112 10-2*8,31*300 ln( 1,00 / 0,250) =138,6 ~139 J. W34 = 4,0112 10-2*8,31*930 ln( 0,25 / 1,00) =-429,7 ~ -430 J. Exprimer et calculer les transferts thermiques sur chacune des transformations. L'énergie d'un gaz parfait ne dépend que de la température. Au cours d'une transformation isotherme, l'énergie interne du gaz parfait ne varie pas. DU12  = 0 ; DU12 =W12 +Q12 d'où Q12 = -W12 ; de même Q34 = -W34. DU23  =W23 +Q23 =Q23 =n Cvm ( T3-T2) =4,0112 10-2* 21 (930-300) =53,07 ~53,1 J. De même : Q41 =n Cvm ( T1-T4) =4,0112 10-2* 21 (300-930) = -53,07 ~ -53,1 J. Définir et calculer le rendement du moteur décrivant ce cycle.   Wmec =W12 +W34 = -nR(Tc-Tf) ln(V1/V2) ; h = |Wmec |/ (Q34 +Q23) = (430-139) / (430+53,1) =291 / 483 =0,602 ~0,60 ( 60 %). Exprimer le rendement du moteur suivant le cycle de Carnot dont les températures des sources chaude et froide sont le mêmes que celles du cycle étudié ici. Conclure et expliquer. h = 1-Tf / Tc = 1-300 / 930 = 0,677 ~0,68 ( 68 %). Le cycle de Carnot est un cas idéal dans lequel toutes les transformations sont réversibles. Il indique quel est le rendement maximal possible. Les transformations réelles ne sont pas réversibles. Dans la réalité, l'hypothèse faite " récupérer totalement la quantité d'énergie échangée par chaleur  lors du  refroidissement isochore pour la restituer au cours du chauffage isochore", est en réalité impossible à réaliser  sur le plan pratique. Il faudrait pour cela que le  régénérateur ait une efficacité de 100 %.

menu