|
|
Certaines
méthodes de détermination de l'indice de réfraction sont largement
inspirées des techniques de la pétrographie ( optique minérale en
particulier ). Pour l'étude d'un fragment de verre ou d'une roche on
prépare une lame mince en déposant sur une lamelle de verre des
fragments du matériau à étudier ( obtenus par écrasement ) et noyés
dans un liquide d'immersion. On recouvre la préparation d'une deuxième
lamelle de verre. On observe ensuite cette lame mince au microscope en
faisant la mise au point sur l'échantillon.
On constate alors que les fragments sont plus ou moins marqués
par un cercle noir : on parle alors du relief de l'échantillon. La lame
mince est éclairée par le bas en lumière parallèle. On ne tiendra pas
compte des lamelles de verre entourant la préparation. On suppose les
fragments et le liquide totalement transparents. Enfin la mise au point
est faite au niveau de la face supérieure du grain ( plan repéré en
pointillés ).
On considère un fragment de verre d'indice N, baignant dans un liquide d'immersion d'indice ne.
On modèlise les fragments en leur donnant une forme telle qu'une coupe
verticale soit un polygone irrégulier. convexe très aplati. Les grandes
faces sont supposées orthogonales aux rayons incidents.
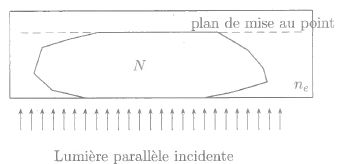
Qu'observerait-on si les in dices du fragment et du liquide d'immersion étaient identiques ? Justifier.
Vis
à vis de la réfraction, le liquide d'immersion et le fragment ayant les
mêmes indices de réfraction, se comporteraient comme un milieu unique
d'indice N : il n'y aurait donc pas de déviation des rayons.
n1 sin i1 = n2 sin i2 ; si n1 = n2 alors i1 = i2.
On cherche à interpréter l'existence des cernes noirs dans l'hypothèse où N > ne.
Reproduire le schéma et tracer l'allure du cheminement des rayons lumineux pour des valeurs N1 puis N2 de N en faisant l'hypothèse que N1 < N2. Dans on suppose l'existence d'un rayon réfracté à travers la face supérieure du fragment pour chaque rayon incident. Justifier l'existence de cernes noires.
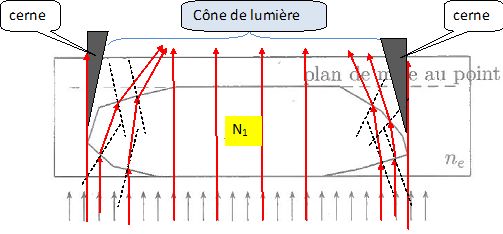
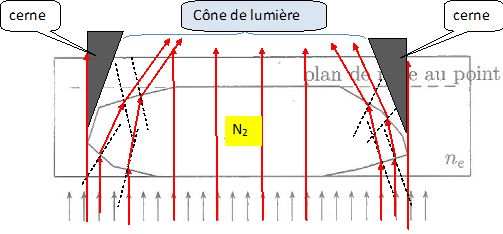
Préciser la relation qualitative entre leur épaisseur et la différence entre les indices du fragment et du liquide d'immersion.
Si N est très différent de ne, la taille des cernes augmentent, les rayons émergents étant plus déviés.
Si N est très proche de ne, la taille des cernes est faible, les rayons émergents étant peu déviés.
|
| .
. |
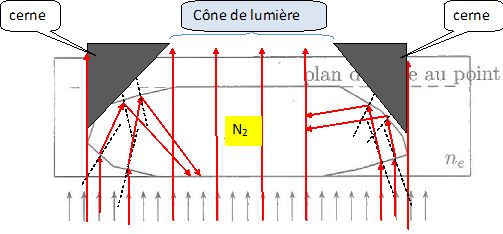
Quel
phénomène supplémentaire peut intervenir au niveau de la face
supérieure si l'écart entre les indices devient très important ? A-t-il
tendance à augmenter ou diminuer l'épaisseur des cernes ?
On peut observer la réflexion totale sur la face supérieure. La taille des cernes va augmenter.
On fait maintenant l'hypothèse que N < ne. Que peut-on en conclure ?
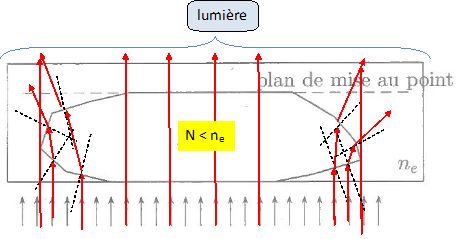
Il n'y a plus de cernes noirs si l'indice du fragment est plus petit que celui du liquide.
On
défocalise le microscope, c'est à dire que la mise au point ne se dait
plus au niveau de la surface du fragment, mais au dessus : cela revient
à abaisser la platine porte-lame du microscope. On voit alors
apparaître une frange brillante le long du contour du fragment, elle
porte le nom de frange ou de liseré de Becke.
Interpréter l'existence de cette frange.
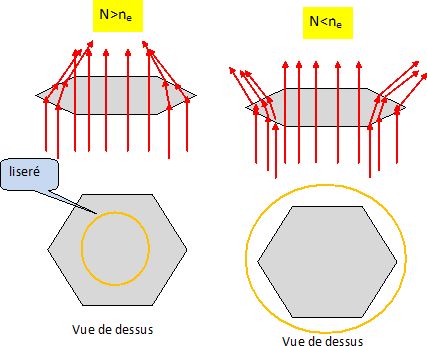
Lorsqu'on abaisse la platine le liseré se déplace dans le milieu le plus réfrigent, celui qui a l'indice optique le plus grand.
On dispose d'un ensemble de liquides d'immersion d'indices de réfraction connus et variés.
Décrire un protocole permettant de déterminer l'indice du fragment. Quelles sont les limites de cette méthode ?
On immerge quelques grains dans un liquide et
on les examine au microscope, en lumière monochromatique. Faire la mise
au point sur la ligne de séparation minéral-liquide.
Faire varier la mise au point jusqu'à ce qu'une fine bande de lumière claire ( liséré lumineux) apparaisse.
Lorsqu’on élève le tube du microscope la frange se déplace : elle pénètre dans le milieu dont l’indice est le plus élevé.
En comparant ainsi le minéral à une série de liquides d’indices
croissants on arrive à trouver deux liquides dont les indices encadrent
celui de la substance.
Cette méthode nécessite de posséder un grand nombre de liquides ou de mélanges de liquides d'indice parfaitement connus.
Jusqu'à
présent on a considéré que la lumière blanche était monochromatique. Il
n'en est biensûr rien, et cela va avoir des conséquences dans les
observations.
Quel
est le phénomène qui fait que deux rayons icidents, de fréquences
différentes et donc de longueurs d'onde dans le vide différentes,
arrivant sur un système optique suivent en général des trajets
différents ?
La célérité
de la lumière dans un verre, donc l''indice de réfraction du milieu,
dépendent de la fréquence : le verre est un milieu dispersif pour la
lumière blanche.
La figure suivante montre l'utilisation d'un prisme de verre ( N ~ 1,5) dans l'air éclairé en lumière blanche.

En déduire le sens de variation de l'indice de réfraction avec la longueur d'onde dans le vide.
Le rouge est le mons dévié ; or sin i2 = ne /N sin i1 : à i1 fixé, i2 est d'autant plus faible que N est plus grand La déviation est égale à D = |i1-i2|. En conséquence la déviation est plus grande qu'en N augmente.
L'indice de réfraction du milieu augmente du rouge au bleu.
On admet la généralité de ce résultat à tous les matériaux étudiés ici.
Un liquide d'immersion donné admet une expression approchée de son
indice de réfraction en fonction de la longueur d'onde exprimée en µm,
suivant la formule de Cauchy : n(l) = A + B / l2. A = 1,466 et B = 0,02133 µm-2.
Pour un fragment particulier on a mesuré les couples (n, l ) suivants :
longueur d'onde (nm)
|
450
|
500
|
550
|
600
|
650
|
700
|
750
|
indice N du fragment
|
1,553
|
1,549
|
1,546
|
1,544
|
1,542
|
1,540
|
1,539
|
indice n du liquide ( calcul à partir de la formule de Cauchy)
|
1,571
|
1,551
|
1,536
|
1,525
|
1,516
|
1,509
|
1,504
|
Tracer sur un même graphe les deux courbes n(l) du liquide et du fragment.
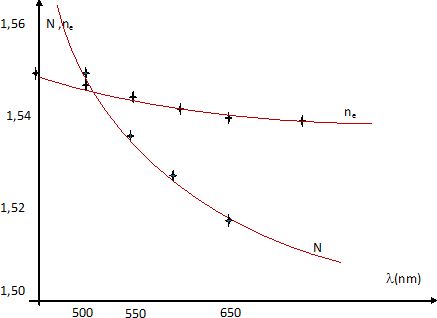
Quelle
devrait être la longueur d'onde d'une lumière monochromatique éclairant
la lame mince pour que le fragment semble invisible ?
L'indice du fragment et celui du liquide d'immersion doivent être
identiques. L'intersection des deux courbes donne environ li =520 nm.
On abaisse la platine pour observer la frange de Becke avec une lumière monochromatique de longueur d'onde l < li. Dans quelle direction se déplace la frange ?
L'indice du liquide d'immersion est supérieur à celui du fragment. La
frange se déplace vers le liquide d'immersion, milieu le plus
réfringent.
Même question si l > li.
L'indice du
liquide d'immersion est inférieur à celui du fragment. La frange se
déplace vers l'intérieur du gragment, milieu le plus réfringent.
Décrire ce que l'on observe en lumière blanche.
Le liseré n'est pas une ligne fine. On observe un étalement de la frange colorée avec les couleurs de l'arc en ciel.
|
|







