|
|
On
génère les ions à l'aide d'une brève impulsion laser dirigé sur une
cible fabriquée à partir de l'échantillon à analyser. Ceci provoque la
vaporisation et l'ionisation de l'échantillon. Les cations ainsi créés
sont accélérés dans un premier temps par une différence de
potentiel imposée entre deux plaques dans une zone où règne un champ
électrique E0 uniforme et stationnaire, c'est à dire
constant dans le temps. Les ions passent ensuite dans une seconde zone,
dite zone de vol libre, dans laquelle ne règne aucun champ
électrique. Ils viennent alors frapper un détecteur qui enregistre le
nombre d'ions ainsi que le temps de vol ( temps écoulé entre
l'impulsion laser et la détection ).
On négligera
l'influence de la pesanteur sur le mouvement des particules chargées.
On rappelle qu'une charge électrique q placée dans un champ électrique
E est soumise à une force électrique 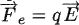 . .
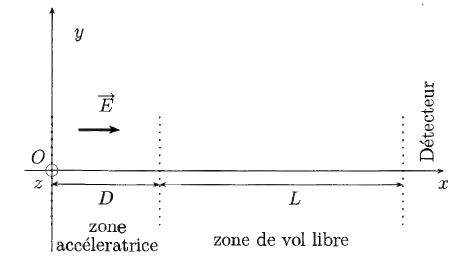
On étudie
l'accélération des ions. On considère un ion de masse m, de charge q,
initialement immobile en x=0, frontière gauche de la zone
accélératrice. Le champ électrique n'existe qu'ntre les plans
d'équations x=0 et x =D. Dans toutes les questions on exprimera les
résultats en fonction des paramètres pris parmi q, m, D, E0 et t.
Ecrire le principe fondamental de la dynamique appliqué à l'ion dans le référentiel du laboratoire supposé galiléen.
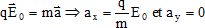
En déduire les équations horaires décrivant le mouvement. Quelles sont la nature du mouvement et la trajectoire ?
La vitesse est une primitive de l'accélération. La vitesse initiale étant nulle, les constantes d'intégration seront nulles.
vx = q/m E0 t ; vy = vz = 0.
La position est une primitive de la vitesse.La position initiale étant le point O, les constantes d'intégration seront nulles.
x(t) = ½q/m E0 t2 ; y(t) = z(t) = 0.
Le mouvement est rectiligne uniformément accéléré.
A quelle date t1 l'ion arrive-t-il en x=D ? Exprimer successivement la vitesse v1 et l'énergie cinétique Ec1 à cet instant.
D = ½q/m E0 t12 ; t1 = (2D m / (qE0))½ ; v1 =q/m E0 t1 =(2D q E0 / m)½ ; Ec1 = ½mv12 = D q E0.
Même question avec un autre ion de charge q et de masse m'.
t'1 = (2D m' / (qE0))½ ; v'1 =q/m' E0 t'1 =(2D q E0 / m')½ ; E'c1 = ½mv'12 = D q E0.
Comparer Ec1 et E'c1 et proposer une explication.
Ec1 = E'c1
; l'énergie cinétique initiale est nulle; la variation de l'énergie
cinétique est égale au travail de la force électrique W = qE0 D. Ce travail est indépendant de la masse des ions.
Quelle est la nature du mouvement d'un ion dans la zone de vol libre ?
Le
poids de l'ion est négligé, la force électrique est nulle en abscence
de champ électrique. La somme des forces étant nulle, le principe
d'inertie indique que le mouvement est rectiligne uniforme.
En déduire le temps de vol tv de l'ion.
tv = L / v + t1= L ( m / (2D q E0) )½ + (2D m / (qE0))½ .
|
| .
. |
Montrer que le rapport masse sur charge de l'ion s'exprime par : 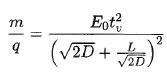
tv2 = L2 ( m / (2D q E0) + 2Lm / (qE0)+ 2D m / (qE0) = m/ q [L2 /(2D E0) + 2L / E0 +2D / E0] = m/ q [L2 /(2D) + 2L +2D] /E0.
m / q = E0 tv2 / [L2 /(2D) + 2L +2D] = E0 tv2 / [L/(2D)½ +(2D)½]2.
L'une des caractéristiques d'un spectromètre est sa résolution, c'est à
dire sa capacité à distinguer deux ions dont les rapports masse sur
charge sont différents mais proches.
La distance D est limitée. Comment
faut-il choisir L pour avoir la meilleur résolution possible, sachant
que la précision sur la mesure du temps est limitée ?
L apparaît au dénominateur, il faut la choisir la plus petite possible, afin que le rapport m/q soit le plus grand possible.
Soient deux ions identiques, émis au même instant, sans vitesse initiale, l'un à l'abscisse x=0 et l'autre à l'abscisse x = Dx différent de zéro. On note tv le temps de vol du premier et t'v celui du second.
Quelle est la distance sur laquelle le deuxième ion est accéléré ? En déduire t'v.
Le deuxième ion est accéléré sur la distance D-Dx. Dans l'expression de tv remplacer D par D-Dx.
t'v = L / v + t1= L ( m / (2(D-Dx) q E0) )½ + (2(D-Dx) m / (qE0))½ .
On suppose que Dx << D. Exprimer l'écart Dtv entre les deux temps de vol en fonction de m, q, E0, D et Dx.
t'v = L ( m / (2D(1-Dx/D) q E0) )½ + (2D(1-Dx/D) m / (qE0))½ . 1 / (1-e)½~1+½e, e étant petit devant 1.
t'v =(1+½Dx/D) [L ( m / (2D q E0) )½ ] + (1-½Dx/D) [2D m / (qE0))½ ] ;
t'v = L ( m / (2D q E0) )½ + 2D m / (qE0))½ + ½Dx/D [L ( m / (2D q E0) )½ -(2D m / (qE0))½ ]
t'v = tv = ½Dx/D [L ( m / (2D q E0) )½ -(2D m / (qE0))½ ]
t'v - tv = ½Dx/D [L ( m / (2D q E0) )½ -(2D m / (qE0))½ ]
Comment faut-il choisir L, à D fixé, pour que les deux ions étudiés arrivent en même temps sur le détecteur, et ne soient pas vu comme deux ions différents. On dit qu'on a réalisé la focalisation spatiale des ions.
L ( m / (2D q E0) )½ -(2D m / (qE0))½ = 0.
L2m / (2D q E0) =2D m / (qE0) ; L2 / (2D) =2D soit L = 2D.
Vérifier que le temps de vol est donné par tv = 2(mL/(qE0)½.
tv = L( m / (2D q E0) )½ + (2D m / (qE0))½ = ( m 4D2/ (2D q E0) )½ + (2D m / (qE0))½ = 2 (2D m / (qE0))½ = 2(mL/(qE0)½.
Cette contrainte sur L reste compatible avec le fait que m/q doit être grand.
Le fait que l'abscisse initiale de l'ion ne soit pas nécessairement
nulle est due au fait que la cible n'est pas infiniment fine.
Quels autres phénomènes, lors de la vaporisation et de l'ionisation, peuvent intervenir et diminuer la résolution du dispositif ?
Lors de la vaporisation et de l'ionisation, certains ions peuvent être
éjectés de la cible avec des vitesses de directions quelconques.
Le réflectron. Il permet d'améliorer très sensiblement la résolution.
A t=0, des ions de masse m, de charge q sont en un point S, et ont une énergie cinétique Ec.
Leur vecteur vitesse est colinéaire à Ox et dirigé dans le sens des x
croissants. Ils volent dans une zone dépourvue de champ sur une
longueur L1. Ils pénètrent dans une zone de réflexion dans
laquelle règne un champ électrique constant E. Sous l'effet répulsif de
ce champ, ils rebroussent chemin après avoir pénétrés jusqu'à une
profondeur maximale dr dans cette zone. Ils retournent dans la zone dépourvue de champ et atteignent le détecteur.
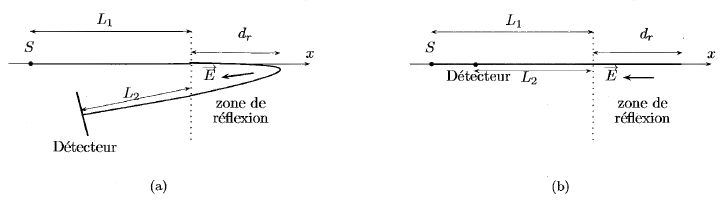
Le champ E sans être colinéaire au vecteur unitaire de l'axe Ox, de
manière à diriger ce flux d'ions vers les détecteurs et non vers la
source, en est cependant très proche. On écrira donc 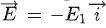 , avec E1
une constate positive. On négligera dans cette étude, en conséquence,
tous les déplacements suivant les directions perpendiculaires à Ox. Le
détecteur est donc placé lui aussi sur l'axe Ox. Cette situation
idéalisée est représentée sur le schéma b. On rappelle que l'on ignore
l'nfluence de la pesanteur. , avec E1
une constate positive. On négligera dans cette étude, en conséquence,
tous les déplacements suivant les directions perpendiculaires à Ox. Le
détecteur est donc placé lui aussi sur l'axe Ox. Cette situation
idéalisée est représentée sur le schéma b. On rappelle que l'on ignore
l'nfluence de la pesanteur.
Exprimer la vitesse v initiale des ions en fonction de Ec. En déduire l'expression du temps t1 que met l'ion pour parcourir la distance L1. Avec quelle vitesse l'ion arrive t-il dans la zone de reflexion ?
Ec = ½mv2 ; v = (2Ec / m)½.
La zone étant dépourvue de champ, le mouvement d'un ion est rectiligne uniforme et t1 = L1/v =L1 (m / (2Ec))½. L'ion arrive avec la vitesse v dans la zone de reflexion.
On montre en changeant l'origine des temps de manière à ce qu'à t=0 les
ions pénètrent dans la zone de réflexion, que, dans cette zone,
l'équation horaire du mouvement des ions est donné par :
x(t) = t (2Ec / m)½-qE1/(2m)t2.
En déduire le temps que passent les ions dans la zone de réflexion.
0= tr (2Ec / m)½-qE1/(2m)t2 ; (2Ec / m)½-qE1/(2m)t =0 ; tr = (2Ec / m)½ 2m / (qE1) =2 (2mEc)½ / (qE1).
Exprimer dr en fonction de Ec, q et E1.
Lorsque la vitesse s'annule, les ions rebroussent chemin : t = ½tr.
dr = (2mEc)½ / (qE1) (2Ec / m)½-qE1/(2m) (2mEc) / (qE1)2.
dr =2Ec / (qE1) -Ec / (qE1) =Ec / (qE1).
Avec quelle vitesse les ions ressortent-ils de la zone de réflexion ? En déduire l'expression du temps t2 que met l'ion pour parcourir la distance L2.
Ils ressortent de cette zone avec la même vitesse qu'ils avaient à l'entrée : v = (2Ec / m)½.
Pour atteindre de détecteur ils sont dans une zone où ne règne aucun champ, leur mouvement est donc rectiligne uniforme.
t2 =L2/v =L2 (m / (2Ec))½.
Exprimer le temps total t mis par les ions pour atteindre les détecteurs depuis S.
t = t1 +tr +t2 =(L1+L2) (m / (2Ec))½ +2 (2mEc)½ / (qE1) avec qE1 =Ec /dr.
t =(L1+L2) (m / (2Ec))½ + 4dr(m / (2Ec))½ = (m / (2Ec))½(L1+L2 + 4dr).
|
Il est possible de choisir la valeur de E1
de manière à réaliser une focalisation en énergie cinétique, c'est à
dire que si des ions partent de S au même instant, mais avec des
énergies cinétiques légèrement différentes de Ec, alors ils arrivent quand même, en première approximation, en même temps au niveau du détecteur.
Calculer la variation Dt du temps de vol, lorsque l'énergie cinétique Ec varie de DEc. En déduire la valeur du champ E1 pour assurer une focalisation en énergie cinétique. Vérifier que cela se traduit par L1+L2 = 4 dr.
(L1+L2) (m / (2Ec))½ +2 (2mEc)½ / (qE1)
dt / dEc=(L1+L2)(½m)½ (-1/(2Ec3/2) + (2m)½ / (qE1) Ec-½ =0.
(L1+L2)(½m)½ (-1/(2Ec) + (2m)½ / (qE1) =0.
(L1+L2) (-1/(2Ec) + 2 / (qE1) =0.
E1 =2Ec /(q(L1+L2)) avec qE1 =Ec /dr.
E1 =4E1dr /(L1+L2) ; 1 =4dr /(L1+L2) ; (L1+L2) =4dr.
Déterminer
l'écart d'énergie cinétique, en fin d'accélération, entre un ion
partant sans vitesse initiale de l'origine, et un ion partant lui aussi
sans vitesse initiale, mais de l'abscisse Dx.
Ion partant de l'origine : Ec1 =qE0D.
Ion partant de l'abscisse Dx : Ec2 =qE0(D-Dx).
Ecart en énergie cinétique : Ec1 - Ec2 =qE0Dx.
|
|
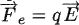 .
.
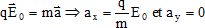
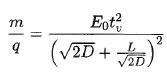

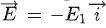 , avec E1
une constate positive. On négligera dans cette étude, en conséquence,
tous les déplacements suivant les directions perpendiculaires à Ox. Le
détecteur est donc placé lui aussi sur l'axe Ox. Cette situation
idéalisée est représentée sur le schéma b. On rappelle que l'on ignore
l'nfluence de la pesanteur.
, avec E1
une constate positive. On négligera dans cette étude, en conséquence,
tous les déplacements suivant les directions perpendiculaires à Ox. Le
détecteur est donc placé lui aussi sur l'axe Ox. Cette situation
idéalisée est représentée sur le schéma b. On rappelle que l'on ignore
l'nfluence de la pesanteur.