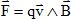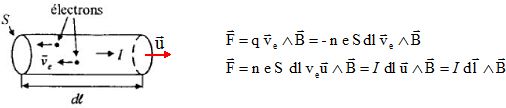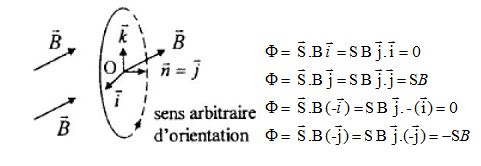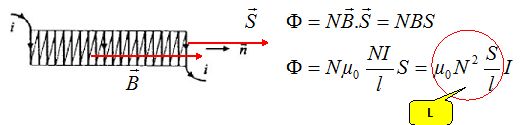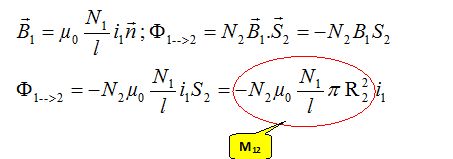|
|
Dans
les systèmes électromagnétiques fonctionnant grâce à la présence d'un
champ magnétique (transformateurs, machines électriques tournantes), le
champ est produit soit par des aimants permanents soit par des circuits
électriques parcourus par des courants.
Quel
procédé expérimental permet de visualiser le spectre magnétique d'un
aimant permanent ou d'un circuit électrique parcouru par un courant ?
On utilise de la limaille de fer : chaque petit morceau de fer se
comporte comme une petite boussole set s'oriente suivant les tangentes
en chaque points aux lignes de champ magnétique.
Qu'appelle-t-on ligne de champ magnétique ?
Le champ magnétique est tangent en chaque point de la courbe appelée ligne de champ.
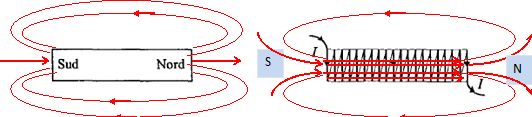
On considère l'aimant parallélépipédique et le solénoïde représentésci-dessous.
Représenter
les lignes de champ à l'extérieur de l'aimant parallélépipédique.
Représenter les lignes de champ à l'extérieur et à l'intérieur du
solénoïde parcouru par le courant I (I > 0). Préciser les pôles Nord
et Sud du solénoïde compte tenu du sens de I.
Qu'appelle-t-on champ magnétique uniforme ?
Un champ est uniforme si sa direction, son sens et sa valeur sont constants : les lignes de champ sont parallèles.
A quelle condition peut-on considérer le champ magnétique uniforme à l'intérieur du solénoïde ?
Le champ à l'intérieur d'un solénoïde est uniforme au voisinage de son axe et loin des extrémités.
Action d'un champ magnétique sur un élément de circuit parcouru par un courant
Expressions des forces magnétiques.
Lorsqu'une particule chargée de charge q se déplaçant à la vitesse v
est plongée dans un champ magnétique B, elle est soumise à la force
magnétique de Lorentz : 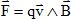
Dans un conducteur métallique parcouru par un courant électrique
d'intensité I, le courant qui circule dans un sens donné correspond à
un déplacement des électrons libres du métal en sens opposé.
On considère un élément de conducteur rectiligne de longueur dl, de
section S, parcouru par un courant d'intensité I . On admet que tous
les électrons ont une même vitesse ve colinéaire à cet élément.
Déterminer
l'expression de |I| en fonction de e (valeur absolue de la charge d'un
électron), de n (nombre d'électrons fibres par unité de volume) de S et
de ve.
On rappelle que l'intensité I s'écrit par définition I = dq/dt ; dq est
la quantité de charge traversant la surface S pendant l'intervalle de
temps dt infiniment petit.
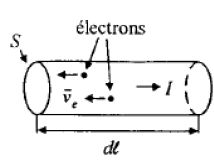
Volume du cylindre : Sdl = S ve dt ; dq = n e S ve dt ; I = n e S ve.
Le
conducteur précédent parcouru par le courant I est soumis à un champ B
uniforme de direction quelconque. On admet que la résultante des forces
magnétiques de Lorentz subies par les électrons libres du volume dl.S
sous l'action du champ B, est intégralement transmise à l'élément
conducteur de longueur dl.
Déterminer cette force résultante appelée force de Laplace.
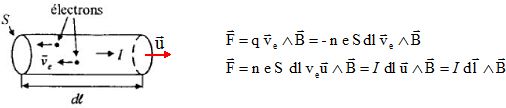
où u est un vecteur unitaire dirigé suivant le conducteur dans le sens de I.
|
| .
. |
Induction électromagnétique.
Formalisation :flux magnétique et force électromotrice d'induction.
Flux magnétique à travers une spire.
Pour un champ B uniforme, le flux magnétique à travers une spire fermée, orientée arbitrairement, est donné par la relation :
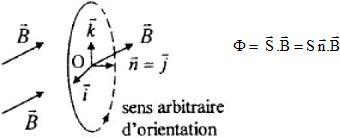
où S est la surface de la spire et n un vecteur unitaire
normal à la spire dont le sens est fixé grâce à la règle du
tire-bouchon en fonction du sens arbitraire d'orientation de la spire
(un tire-bouchon tournant dans le sens d'orientation de la spire
progresse suivant n).
L'unité de flux magnétique est le weber (Wb).
On considère un repère orthonormé de centre O, celui de la spire, de trièdre direct associé (i, j, k).
Préciser l'expression du flux Φ et son signe dans les cas suivants (B>0).
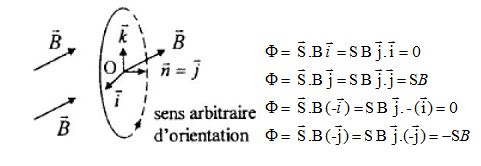
Force électromotrice (f.é.m) induite.
Lorsque le flux Φ traversant une spire varie dans le temps, la spire
est le siège d'une force électromotrice e exprimée en volts. On
constate alors l'apparition d'un courant induit i dans le circuit.
L'expression de e est donnée par la loi de Faraday e = -dF/dt où dΦ est la variation élémentaire du flux dans la spire pendant l'intervalle de temps dt infiniment petit : dΦ= F(t+dt) - F(t).
La f.é.m e est une grandeur algébrique, comptée selon le sens
arbitraire d'orientation de la spire choisi pour calculer Φ ; si e est
positif, le courant induit i, compté dans le même sens que e, est
également positif.
On considère le circuit suivant :
On approche la face Nord d'un aimant d'une spire conductrice qui se
referme sur un galvanomètre G à cadre mobile (il s'agit d'un
ampèremètre destiné à la mesure des courants faibles). On suppose que
le champ B créé par l'aimant est uniforme sur la surface de la spire
(spire de dimension petite par rapport à la section de l'aimant) et on
choisit un sens arbitraire d'orientation de la spire.
Préciser sur un schéma en les justifiant le sens et le signe de la f.é.m d'induction e et du courant induit i.
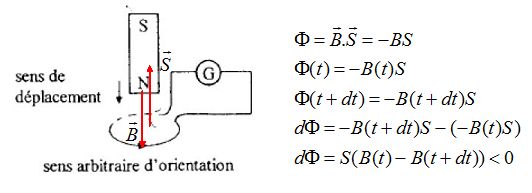
Lors de l'approche du pole nord de l'aimant, le champ magnétique devient plus intense. e = -dF/dt est positive et le courant induit à le sens arbitraire d'orientation.
Dans la loi générale de Faraday qui s'exprime comme ci-dessus, Φ
désigne le flux total à travers un circuit ; il correspond à la somme
du flux propre dû au circuit lui-même et du flux extérieur dû aux
éléments magnétiques environnants.
Loi de Lenz.
Pour étudier d'un point de vue qualitatif le phénomène d'induction
électromagnétique dans un circuit électrique, on fait référence à la
loi de Lenz ou loi de modération : "le courant induit dans le circuit
tend à s'opposer par ses effets à la cause qui lui a donné naissance".
En faisant référence à la loi de Lenz, retrouver le signe du courant induit dans le circuit ci-dessus.
Par ses effets électromagnétiques, le courant induit s'oppose à
l'augmentation du champ magnétique lors de l'approche de l'aimant. Il créé donc un champ
magnétique induit de sens contraire, c'est à dire dirigé verticalement
vers le haut.
Auto-induction.
On considère une bobine parcourue par un courant i supposé positif. Par
convention, on oriente les spires de cette bobine dans le sens de i.
En raisonnant successivement avec la f.é.m d'induction e puis avec la
loi de Lenz, préciser ce qui se passe dans le circuit si le courant i a
tendance à augmenter. On appelle ce phénomène auto-induction.
L'intensité du courant et le champ magnétique étant proportionnels, à
une augmentation de l'intensité correspond à la croissance du champ.
La variation de flux est positive : la fem induite est négative et le courant induit a le sens contraire du courant i.
Ou bien le champ magnétique induit s'oppose à l'augmentation du champ
inducteur : le courant induit a le sens contraire du courant i.
Une bobine s'oppose à la variation de l'intensité du courant.
Auto-inductance et mutuelle inductance.
On montre que le champ B créé par un solénoïde de longueur l
très supérieure à son rayon R, comportant N spires parcourues par un
courant i, s'exprime, à l'intérieur du solénoïde, par : B = µ0 N i / l avec μ0 = 4π.10−7H.m−1
où H est le symbole du Henry. Par convention, on oriente les spires
dans le sens de i ; ceci définit la normale n commune à toutes les
spires.
Déterminer le flux magnétique Φ à travers les N spires du solénoïde. Montrer que Φ est proportionnel à i.
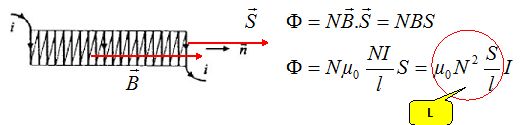
On appelle auto-inductance ou inductance propre et on note L
le coefficient de proportionnalité reliant le flux Φ et le courant i.
Ce coefficient s'exprime en Henry et est toujours positif avec la
convention choisie.
Vérifier
sur l'exemple choisi que ce coefficient ne dépend que des grandeurs
géométriques du circuit étudié et du nombre de spires N.
Application numérique : calculer L pour R = 2 cm, N = 150 spires, l = 30 cm.
S = p R2 =3,14 *(2 10-2)2 = 1,256 10-3 m2.
L = 4 *3,14 10-7 *1502* 1,256 10-3/ 0,30 =1,18 10-4 ~1,2 10-4 H.
On considère deux solénoïdes S1 et S2 comportant respectivement N1 et N2 spires, de rayons respectifs R1 et R2 avec R2 < R1 mais très voisin de R1, de longueur l (l >> R1). Ces deux solénoïdes sont bobinés dans le même sens, ont même axe et le solénoïde S1 est obtenu en bobinant ses spires par dessus celles du solénoïde S2 sur toute la longueur l. Le solénoïde S1 est parcouru par un courant i, tandis que S2 est en court-circuit.
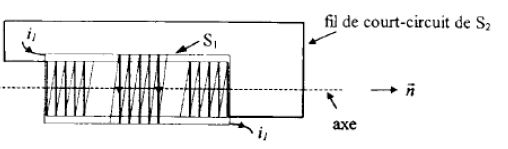
Pour le calcul des flux, la normale n commune aux spires des deux solénoïdes est définie à partir du sens de i1.
Déterminer le flux F1-->2 dû à B1, envoyé par S1 à travers les N2 spires de S2.
B1 = µ0N1 i1/l ; F1-->2 =N2 B1 S2=N2 µ0N1 i1/l S2 = µ0N1N2 i1/l pR22.
En déduire l'expression de la f.é.m induite dans le solénoïde S2 et le sens positif du courant induit i2 pour i1 croissant.
e = -dF1-->2/dt = -µ0N1N2 /l pR22 di1/dt avec di1/dt positif.
e est donc négative et i2 est de sens contraire à i1.
On pose : F1-->2= M21 i1. On appelle mutuelle inductance le coefficient M21.
Déterminer la mutuelle inductance M21 et vérifier qu'elle ne dépend que des nombres de spires et des grandeurs géométriques des circuits.
M21 = µ0N1N2 /l pR22.
Avec les valeurs numériques suivantes : R1 = 2 cm, R2 = 1,8 cm, l = 30 cm, N1 = N2 = 150 spires, calculer M21.
M21 = 4 *3,142 10-7 *1502/0,30 *0,0182 =9,6 10-5 H.
Bilan.
Si on alimente simultanément les deux bobines précédentes (S2 n'étant plus en court-circuit) par des courants i1 et i2, on peut écrire :
F1 = F1-->1 + F2--1.
F2 = F2-->2 + F1--2.
Le flux F1 est le flux total à travers les N1 spires de S1 : il est la somme du flux propre F1-->1 = L1 i1 produit par le courant i1 et du flux F2--1=M12 i2 envoyé par la bobine S2 dans la bobine S1. Pour calculer F1-->1 et F2-->1 on oriente par convention les spires de S1 dans le sens de i1.
De même, le flux F2 est le flux total à travers les N2 spires de S2 : il est la somme du flux propre F2-->2=L2 i2 produit par le courant i2 et du flux F1--2=M21 i1 envoyé par la bobine S1 dans la bobine S2. Pour calculer F2-->2 et F1-->2 on oriente par convention les spires de S2 dans le sens de i2.
Pour déterminer M12 on admettra que le champ magnétique produit par S2 seul est nul dans la zone comprise entre les rayons R2 et R1.
Déterminer L1, L2, M12, M21 si i1 et i2 ont même sens. Quelle est la relation entre M12 et M21 ? Ecrire une inégalité entre L1, L2, M12, M21.
L1 = µ0 N12 p R12/l =1,2 10-4 H. L2 = µ0 N22 p R22/l = 4 *3,142 10-7 *1502 *0,0182 / 0,30 =9,6 10-5 H.
B1 = µ0N1 i1/l ; F1-->2 =N2 B1 S2 =N2 µ0N1 i1/l S2 = µ0N1N2 i1/l pR22. M12 = µ0N1N2/l pR22.
B2 = µ0N2 i2/l ; F2-->1 =N1 B2 S1 = N1 B2 S2= N1 µ0N2 i2/l S2 = µ0N1N2 i2/l pR22. M21 = µ0N1N2/l pR22.
M12 =M21 = 9,6 10-5 H. L1 >= M12>= L2.
Comment sont modifiées M12 et M21 si i1 et i2 ont même sens et si les solénoïdes sont bobinés dans des sens opposés ?
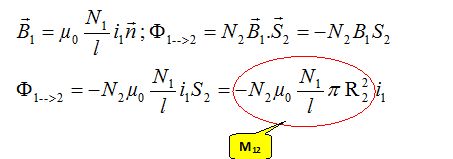
Pour deux circuits C1 et C2 quelconques, on peut montrer que l'on a les deux relations suivantes :
M12 =M21 =M et |M| =k(L1L2)½ avec k coefficient inférieur ou égal à 1 appelé coefficient de couplage.
|
.
|