|
|
Une perturbation
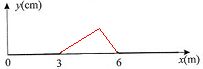
transversale est créée sur une corde tendue Ox. L'allure simplifiée de
la perturbation au cours du temps, à l'origine des abscisses, est
représentée figure 1. Celle de la corde à un instant t=t est représentée figure 2.

A) Parmi les formes d'énergie transportée par l'onde, il y a de
l'énergie cinétique. Vrai.
Une onde transporte de
l'énergie sous forme cinétique, potentielle, élastique ; lors de la
propagation de la perturbation , il y a conversion d'une forme d'énegie
en une autre forme.
B) La célérité de l'onde vaut 2 m/s.Vrai.
(6-3) / 1,5 = 2 m/s.
C) L'allure de la corde est représentée à l'instant t = 3 s. Faux.
En trois secondes, la
perturbation atteint le point d'abscisse 3*2 = 6 m. Sur la figure 2 la forme de la
perturbation n'est pas respectée.
D) Si l'on augmente la tension de la corde, la célérité de l'onde sera
augmentée. Vrai.
célérité = racine carrée
( tension / masse linéïque).
Un vibreur met en mouvement une corde de longueur L = 10 m. On compte n
= 10 oscillations du vibreur pendant une durée t1 = 20 s. L'onde met
une durée t2= 2,0
s pour atteindre l'extrémité de la corde.
A) la fréquence des oscillations est f = 0,50 Hz.Vrai.
fréquence = nombre
d'oscillations en une seconde soit 10/20 = 0,50 Hz.
B) la célérité des ondes sur la corde est v = 5,0 m/s.Vrai.
L'onde parcourt 10 m en
2,0 s ; v = 10/2,0 = 5,0 m/s.
C) Avec une corde de même longueur, plus lourde, tendue de la même
façon, la longueur d'onde l
serait plus grande. Faux.
La masse linéïque de la corde augmente et
en conséquence la célérité diminue.
Or l = v / f, f étant constante, v diminuant,
alors la longueur d'onde diminue.
D) La fréquence f dépend de l'amplitude des socillations. Faux.
Un échantillon de l'isotope 2411Na a une
activité A = 9,0 106 Bq. Il y a émission d'un électron
lors de sa désintégration radioactive. La demi-vie du nucléide est t½
= 15 h.
A) Il s'agit d'un émetteur alpha. Faux.
L'émission d'un électron
correspond à une radioactivité de type béta moins.
B) L'expression de la constante radioactive est l = ln2 / t½.Vrai.
C) Le noyau formé est l'isotope 2410Ne du néon. Faux.
2411Na
---> 2412Mg+0-1e.
D) Au bout de 45 h, l'activité n'est plus que de 3,0 106 Bq. Faux.
45 h = 3 *15 = 3
demi-vie. Au bout de trois demi-vie l'activité initiale est divisée par
23 = 8. |
| .
. |
Une réaction nucléaire dans le soleil entre un noyau de
deutérium 21H et un noyayu de tritium 31H
conduit à la formation d'un noyau d'hélium 4 42He.
Noyau
|
21H |
31H |
42He |
El/A
(MeV/ nucléon)
|
1,183
|
2,825
|
7,074
|
A) Il s'agit d'une réaction de fusion thermonuléaire.Vrai.
B) Il y a émission d'un proton au cours de cette réaction. Faux.
21H + 31H ---> 42He + 10n. ( émission d'un neutron ).
C) L'énergie de liaison du noyau 21H est : El
=(mproton + 2 mneutron - mdeutérium) c2. Faux.
Le noyau de deutérium compte un
proton et un seul neutron : El =(mproton + mneutron - mdeutérium) c2.
D) L'énergie libérée par la réaction est 3,066 MeV. Faux.
7,074*4 -2,825*3-1,183*2
=28,296-8,475- 2,366 = -17,4 MeV.
Afin d'étudier la diffraction et observer l'influence
de la largeur de la fente utilisée sur la largeur d de la tache
centrale de diffraction, on dispose :
- d'une source laser de longueur d'onde l ;
- d'un support sur lequel seront placés successivement des fentes de
largeurs a différentes. Le plan de la fente est perpendiculaire au
faisceau laser.
- d'un écran d'observation placé parallèlement au plan de la fente à
une distance D = 2,5 m de celui-ci.
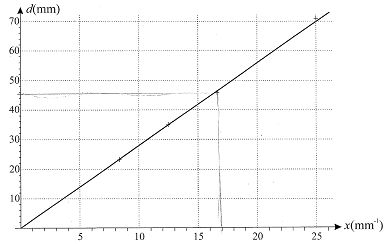
On trace le graphe ci-dessous d=f(x) où x = 1/a est l'inverse de la
largeur des fentes calibrées.
A) L'angle sous lequel on voit la tache centrale depuis la fente est q = 2 l/D. Faux.
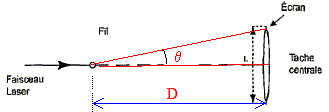
tan q = ½L/D voisin de q radian pour les angles petits.
d'autre part q = l/a.
avec : l longueur d'onde (m) et a : diamètre du
fil (m)
en tenant compte des deux
relations ci-dessus : ½L/D=l/a soit a=2lD/L ou L =d = 2l D/a.
B) L'expression du coefficient directeur de la droite est k = 2lD.Vrai.
C) k = 2,8 mm2.Vrai.
28 / 10 = 56 /20~2,8 mm2.
D) l~ 560 nm.Vrai.
k = 2
l D ; l = k/(2D) = 2,8 10-6
/5 =5,6 10-7 m = 560 nm.
Soit
un circuit LC idéal, siège d'ozcillations périodiques. La bobine a une
inductance L = 0,50 H et la condensateur une capacité C = 10 mF.
A la date t=0, la tension aux bornes du condensateur est UCm = 4,0 V.
p 2½~4,5 ; 2p 2½~8,9.
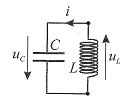
A) A tout instant, on peut écrire uC + uL = 0.Vrai.
Additivité des tensions aux bornes d'appareils en série.
B) La période propre est T0~4,5 10-2 s. Faux.
T0 = 2 p (LC)½ = 2 p (0,50 *10 10-3)½ = 2 p (2*25 10-4)½ = 2 p *5 10-2*2½ ~0,1*4,5 = 0,45 s.
C) La tension aux bornes du condensateur ( en volts) a pour expression uc(t) = 4,0 cos (14 t).Vrai.
w = 2 p / T0 = 2 p / (2 p *5 10-2*2½ ) =100/ (5 *2½ )~14 rad/s ; amplitude UCm = 4,0 V.
D) L'intensité du courant ( en ampère) a pour expression : i(t) = 56 sin ( 14t). Faux.
i(t) = dq/dt = Cduc/dt = -C*4,0*14 sin ( 14t) = -0,010*4,0*14 sin (14t) = -0,56 sin (14t).
|
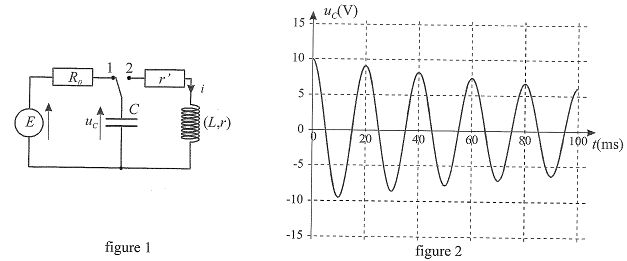
L'étude
d'un circuit RLC est effectuée avec un système d'acquisition relié à un
ordinateur qui permet de suivre l'évolution de la tension uc
aux bornes du condensateur. Sur le schéma de la figure 1 l'interrupteur
est en position 1 depuis longtemps quand on bascule l'interrupteur en
position 2 à l'instant t =0. L'enregistrement obtenu est celui de la
figure 2. C = 0,1 µF et p2 ~10.
A) A l'instant t = 0+, l'intensité i =uc/(r+r'). Faux.
La continuité de l'intensité à travers la bobine conduit à t(0) = t(0+) = 0.
B) L'expression de l'intensité est i(t) = 1/C duc/dt. Faux.
i(t) = -dq/dt = - C duc/dt.
C) L'expression approchée de la pseudo-période est T ~2p(L / C)½. Faux.
T ~2p(L C)½.
D) L'énergie électrique emmagasinée à t=0+ dans le circuit est 0,5 µJ. Faux.
Continuité de l'énergie stockée dans le condensateur : ½ Cuc(t=0)2 = 0,5 10-7 *102 =0,5 10-5 J = 5 µJ.
|





