Etude d'une bobine, oscillations électriques : concours EMCTA 2010. Ecole Militaire des corps techniques et administratifs

. .

Etude d'une bobine. On considere le circuit suivant, réalisé avec une bobine d'inductance L = l0 mH et de résistance interne r= 5 ohms, une résistance R=45 ohms, un intemrpteur K et un générateur de E tension continue de force électromotrice E = 5 V. A l'aide d'un dispositif d'acquisition informatique adapté, on enregistre l'évolution de I'intensité i(t) du courant dans le circuit. L'instant initial est celui où l'on ferme l'intemrptanr K. Reproduire le schéma du circuit sur votre copie en indiquant les branchements à effectuer pour visualiser en voie A d'un oscilloscope l'évolution de la tension aux bomes de la bobine {L, r}. Par I'intermédiaire de quelle tension peut-on suivre l'évolution de I'intensité du courant dans le circuit ? Indiquer sur le schéma le branchement de la voie B de l'oscilloscope permettant de visualiser cette tension et donner la relation entre cette tension et i(t). La tension aux bornes d'un conducteur ohmique et l'intensité du courant sont proportionnelles. L'image de cette tension et l'image de l'intensité au facteur R près. A I'aide du dispositif informatique, on o'tient directement l'évolution de i(t), la courbe enregistrée est la suivante : Déterminer graphiquement la constante de temps t du dipôle RL en précisant la méthode utilisée. . . Mpntrer que l'équation diférentielle à laquelle obéit l'intensité i(t) dans le circuit est : di/dt +(r+R)/L i = E/L. 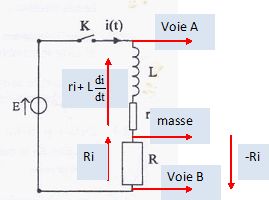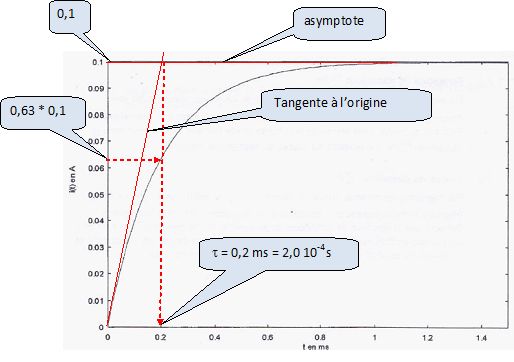Additivité des tensions : E = Ldi/dt +ri + Ri. Diviser chaque terme par L, d'où : di/dt +(r+R)/L i = E/L. La solution de cette équation peut être proposée sous la forme i(t) = A exp(-t/t) + B. Exprimer les constantes A et B et t en fonction des données. Dériver i(t) par rapport au temps : di/dt = -A / t exp(-t/t). Repport dans l'équation différentielle : -A / t exp(-t/t) +(r+R) / L (A exp(-t/t) + B) = E/L. A(-1 / t +(r+R) / L )exp(-t/t) + B(r+R) / L = E/L. Par identification : -1 / t +(r+R) / L = 0 soit t = L/(r+R) et B = E/(r+R). Calculer numériquement la constante de temps t et comparer votre valeur à celle obtenue graphiquement. t =0,01 / 50 = 2,0 10-4 s ( valeur identique à celle du graphique ). 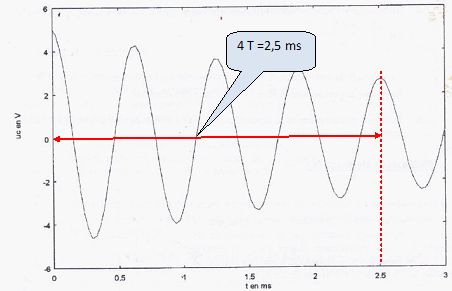Oscillations électriques. On modifie le circuit précédent en remplaçant le générateur de tension continue par un condensateur de capacité C = 1 µF initialement chargé sous une tension de 5 V et en remplaçant la résistance R par une résistance variable Rv. A l'instant t = 0 s, on ferme K. On suppose tout d'abord que la résistance totale du circuit est négligeable (r + Rv = 0), on a donc un condensateur et une bobine parfaite associée en série. 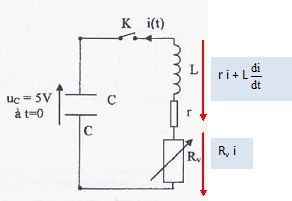Etablir l'équation différentielle regissant l'évolution de la tension uc(t) aux bomes du condensateur. Additivité des tensions : uc(t) + Ldi/dt +ri + Rvi = 0. or i = dq/dt et q = Cuc soit i = C duc/dt et di/dt = C d2uc/dt2. uc(t) + LC d2uc/dt2 +(r+Rv) C duc/dt= 0. Si (r+Rv) ~0, alors : uc(t) + LC d2uc/dt2 = 0. (1). Montrer que l'expression suivante uc(t) = U0 cos(2pt / T0) est une solution de cette équation compatible avec les conditions initiales. à t = 0 uc(0) = 5 V : 5 = U0 exp(0) = U0. Déterminer I'expression littérale de T0 et la valeur de U0. duc(t) /dt = -U0 2p / T0 sin(2pt / T0) ; d2uc/dt2 =-U0 (2p / T0 )2cos(2pt / T0). Repport dans (1) : U0 cos(2pt / T0) -LC U0 (2p / T0 )2cos(2pt / T0) =0 1-LC(2p / T0 )2= 0 ; T0 = 2 p (LC)½. Calculer numériquement T0 en prenant p = 3,14. T0 = 2 *3,14 (10-2 *10-6)½ = 6,28 10-4 ~6,3 10-4 s = 0,63 ms.. En réalisant le montage expérimental avec une résistance variable nulle, on obtient l'oscillogramme suivant pour la tension aux bomes du condensateur : Comment appelle-t-on le régime du circuit RLC correspondant à cette situation ? L'amplitude des oscillations diminue au cours du temps : régime pseudo-périodique. Nommer et définir la durée caractistique associée à ce régime. La pseudopériode T. Estimer graphiquemert cette duré et commenter le résultat. T ~2,5 / 4 ~0,625 ~0,63 ms, valeur très proche de T0 : l'amortissement est faible. En augmemant la valeur de la résistance variable, on peut observer deux autres régimes du circnrit RLC. Quels sont leurs noms ? Le régime critique et le régime apériodique.

menu