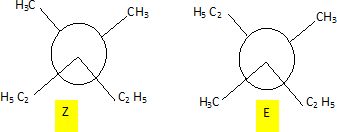
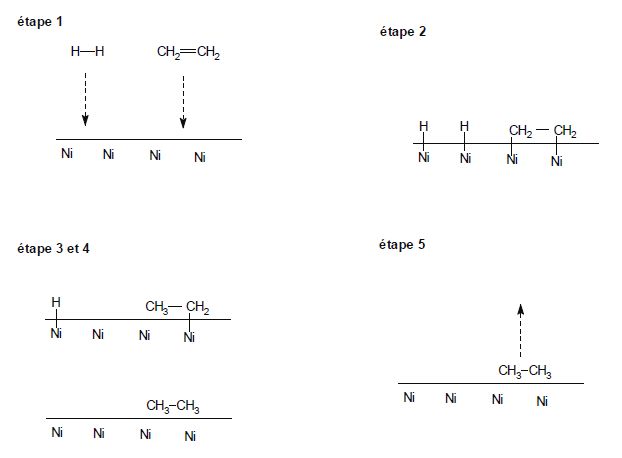
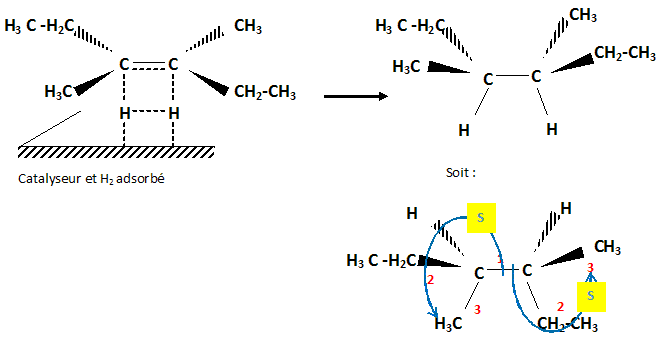
Le nickel de Raney : hydrogénation des alcènes : concours CAPLP maths sciences 2012. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. Données : Produit de solubilité de Al(OH)3 solide à 25°C pKs = 32,3 Constante de complexation globale de [Al(OH)4]- à 25°C : Al3+ (aq) + 4 HO- (aq) = [Al(OH)4]- (aq) log ß4 = 33,4 Constante d’autoprotolyse de l’eau à 25°C Ke = 10-14. Potentiels rédox à 25°C E° (H+ (aq) / H2 (g)) = 0 V ; E° (O2 (g) / H2O (l)) = 1,23 V RT ln10 / F = 0,06 à 25°C. Le nickel de Raney est obtenu par action de la soude concentrée (pour avoir pH > 12) sur un alliage nickel-aluminium de composition massique 50-50. On donne  le diagramme E-pH à 25°C de l’élément nickel pour une concentration en espèces dissoutes 10-2 mol.L-1. Il a été tracé en considérant les espèces Ni(s), Ni2O3(s), NiO2(s), Ni(OH)2(s) et Ni2+(aq). Déterminer le degré d’oxydation du nickel dans les espèces citées ci-dessus puis attribuer chaque espèce à une lettre du diagramme (A à D). Ni est déjà placé. n.o(Ni) dans Ni2O3(s) : 2 n.o(Ni) -2*3 = 0 ; n.o(Ni) = +III. n.o(Ni) dans NiO2(s) :  n.o(Ni) -2*2 = 0 ; n.o(Ni) = +IV. n.o(Ni) dans Ni(OH)2(s) :  n.o(Ni) -2*2+2*1 = 0 ; n.o(Ni) = +II. n.o(Ni) dans Ni2+(aq) :  n.o(Ni) = +II. Écrire la demi équation rédox puis la loi de Nernst pour le couple de l’eau H+ (aq) /H2(g). 2H+ (aq) + 2e- = H2(g) ; E = E°(H+ (aq) /H2(g)) +0,03 log ([H+ (aq)]2 / PH2 ). Écrire la demi équation rédox puis la loi de Nernst pour le couple de l’eau O2(g)/H2O(l).  ½O2(g) + 2H+ (aq) + 2e- = H2O(l). E = E°(O2(g)/H2O(l)) +0,03 log ([H+ (aq)]2 P½O2). En déduire les équations des droites frontières relatives aux couples de l'eau. On prendra PH2 = PO2 = 1 bar. 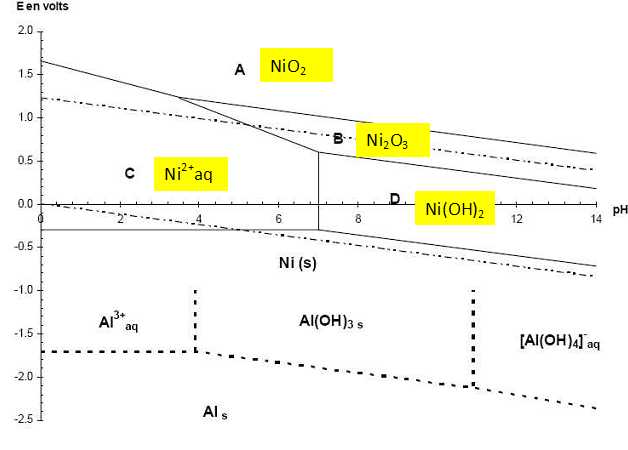E = 0 + 0,03 log ([H+ (aq)]2) = 0,06 log [H+ (aq)] = -0,06 pH. E = 1,23 +0,03 log ([H+ (aq)]2 ). = 1,23 +0,06 log [H+ (aq)] = 1,23 -0,06 pH. Ecrire la demi équation redox relative au couple Ni(OH)2 (s) / Ni(s) puis l'équation de Nernst relative à ce couple. Déterminer le coefficient directeur de la droite frontière puis une méthode de tracé rapide pour les droites frontières de l'eau à partir du diagramme E-pH du nickel. Ni(s)+ 2HO-aq = Ni(OH)2 (s) + 2e-.  E = E°(Ni(OH)2 (s) / Ni(s)) +0,03 log (1 / [HO-aq]2) = E°(Ni(OH)2 (s) / Ni(s)) +0,03 log ( [H+aq]2 / 10-28 ). E = E°(Ni(OH)2 (s) / Ni(s)) +0,06 log ( [H+aq] / 10-14 ) = E°(Ni(OH)2 (s) / Ni(s)) +0,06 log (1014 ) -0,06 pH. Pente de la droite frontière : -0,06. Les droites frontières de l'eau ont le même coefficient directeur que la droite frontière relative à Ni(OH)2 (s) / Ni(s). Ces droites sont parallèles : celle relative à H+ (aq) /H2(g) a une ordonnée à l'origine égale à zéro. Celle relative à O2(g)/H2O(l) a une ordonnée à l'origine égale à 1,23 V. On acidifie une solution contenant l'espèce B. Que se passe-t-il ? ( aucune équation n'est demandée ) Dismutation de B en Ni2+aq et NiO2(s). Ecrire l'équation de la réaction de formation de Al(OH)3 (s). Al3+aq + 3 HO-aq = Al(OH)3 (s). Ks = [Al3+aq] [HO-aq]3 = 10-32,3. Ecrire l'équation de la réaction de dissolution de Al(OH)3 (s). Al(OH)3 (s) + HO-aq = [Al(OH)4]- aq. Montrer que la constante d'équilibre K de la réaction de dissolution peut s'exprimer en fonction  de la constante de solubilité Ks et de la constante de complexation globale ß4 de [Al(OH)4]- aq. Calculer sa valeur. Al3+aq + 4 HO-aq = [Al(OH)4]- aq. ß4 = [[Al(OH)4]- aq] / ([Al3+aq][HO-aq]4) =1033,4. K = [[Al(OH)4]- aq] / [HO-aq] = ß4 [Al3+aq][HO-aq]4/ [HO-aq] = ß4 [Al3+aq][HO-aq]3 = ß4 Ks = 1033,4 * 10-32,3= 12,6. Calculer le pH de fin de dissolution du précipité pour une solution d'ions aluminium Al3+aq  de concentration c0 = 0,01 mol/L. K = [[Al(OH)4]- aq] / [HO-aq]  = 12,6 ; [HO-aq] = [[Al(OH)4]- aq] / K = 0,01 / 12,6 =7,94 10-4 mol/L. pOH = - log (7,94 10-4) = 3,1 ; pH = 14 -pOH = 10,9. A partir des diagramme E-pH, expliquer la méthode de synthèse du nickel de Raney. Traiter un morceau d'alliage nickel-aluminium en poudre par la soude concentrée. La majeure partie de l'aluminium de l'alliage est dissous. La structure poreuse qui en résulte possède une importante surface spécifique. Vers pH 10, couples oxydant/réducteur : [Al(OH)4]- /Al(s) ; Ni(OH)2(s)/Ni(s) ; H2O/HO-. Al(s) et HO- appartiennent à des domaines disjoints. Les domaines relatifs à Ni(s) et HO- ont une partie commune. Les domaines relatifs à [Al(OH)4]- et HO- ont une partie commune. L'aluminium, réducteur le plus fort est oxydé. Le nickel de Raney est concervé dans l'eau, car il est pyrophorique quand il est sec. Que signifie pyrophorique ? Combustion spontanée en présence d'air. Hydrogénation des alcènes. L'hydrogénation d'un alcène A(g) par le dihydrogène est réalisée dans une enceinte fermée de volume V0 à T0 = 800 K à partir d'un mélange équimolaire d'alcène et de dihydrogène. On définit la vitesse de réaction de la manière suivante : A(g) + H2(g) = AH2(g). v = -dp(H2) /dt = -dp(A)/dt =dp(AH2) / dt où p est la pression partielle du gaz. Si on considère que la réaction possède un ordre, la vitesse de la réaction peut s'écrire avec a ( ordre partiel de A ), b ( ordre partiel de H2 ) et k la constante de vitesse : v = k pa(A) pb(H2). On mesure l'évolution de la pression partielle en dihydrogène en fonction du temps. t(s) 0 100 180 300 510 800 2000 p(H2) en bar 1,0 0,90 0,83 0,75 0,64 0,53 0,31 En utilisant la relation des gaz parfait, donner la relation entre la pression partielle p d'un gaz ,n sa quantité de matière, T0 et V0 température et volume du réacteur et R la constante des gaz parfaits. 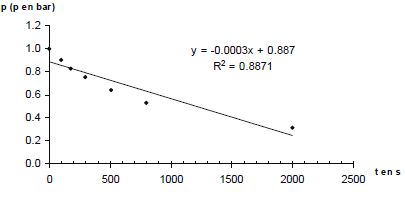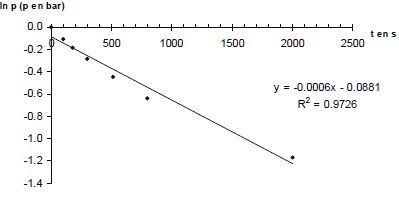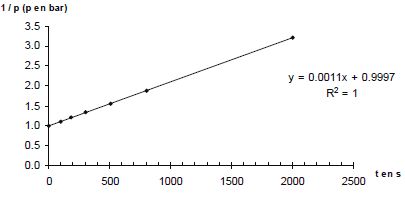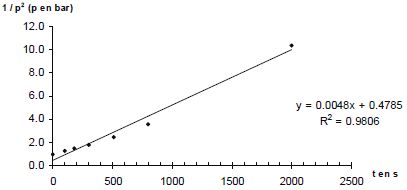p = n RT0 / V0. Donner la relation entre p(A) et p(H2) à tout instant t. En déduire une équation différentielle vérifiée par p(H2). Le mélange initial étant équimolaire et les nombres stoechiométriques relatifs à A et H2 étant les mêmes, p(A) = p(H2). v = k p(H2)a+b ; v = -dp(H2) /dt  ; dp(H2) /dt + k p(H2)a+b  = 0. Si a+b = 1 : p(H2) = constante exp(-kt ) ou ln p(H2) =  ln ( constante) -kt. Si a+b = 2 : p(H2) = B / t + C, B et C sont des constantes. A partir des différentes représentations des résultats expérimentaux, déterminer l'ordre global ( a+b) de la réaction. Pour chaque représentation, une régression linéaire a été effectuée : la droite a été tracée et son équation ainsi que le coefficient de corrélation donnés. 1 / p = f(t) convient, c'est à dire p(H2) = B / t + C : a+b = 2. On a déterminer les temps de demi-réaction pour différentes hydrogénations de A en présence d'un excès de dihydrogène. p(A) en bar à t=0 1,5 1,0 0,5 temps de demi-réaction ( s) 126 126 126 Déterminer l'ordre partiel a de l'alcène puis l'ordre partiel b du dihydrogène. Le dihydrogène étant en excès, p(H2) peut être considérée comme constante et v = k' pa(A) a avec k' =k pb(H2). Le temps de demi-réaction étant indépendant de p(A), l'ordre partiel "a" est égal à 1. Par suite b = 1.   Déterminer l'unité puis la valeur de la constante de vitesse k(800 K). 1/p = 0,0011 t +0,9997 du type 1/p = k t + 1/p0. k = 0,0011 bar-1 s-1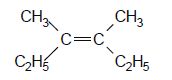. On considère l’hydrogénation de l’alcène A . Cette hydrogénation donne H2A. Donner le nom de l'alcène. (Z) 3,4-diméthylhex-3-ène. Combien de stéréoisomères possède A ? Les représenter en Newman en indiquant la configuration des carbones asymétriques éventuels. Identifier les relations d'isomérie entre ces composés. Il n'y a pas de carbone asymétrique, donc pas d'énantiomères. Il existe un autre diastéréoisomère, le (E) 3,4-diméthylhex-3-ène. L'hydrogénation catalytique de l'alcène A par le nickel de Raney donne un produit majoritaire. Rappeler la définition d'un catalyseur. Un catalyseur est une espèce qui accélére une transformation chimique lente, mais spontanée ; il n'apparaît pas dans le bilan : il est régénéré en fin de réaction. Donner la définition de la catalyse homogène et hétérogène. Catalyse homogène : le catalyseur est dans la même phase que les réactifs. Catalyse hétérogène : le catalyseur et les réactifs sont dans des phases différentes. Sur un catalyseur solide, un réactif gazeux peut s'adsorber à la surface du solide. L'annexe donne un mécanisme pour l'hydrogénation de l'éthène. Donner le nom de chaque étape. - Adsorption des réactifs à la surface du catalyseur. - quand toutes les nouvelles liaisons sont réalisées, le produit peu adhérent au catalyseur se détache de celui-ci par simple agitation thermique. Proposer une explication de la présence du produit majoritaire pour l’hydrogénation catalytique de l’alcène A par le nickel de Raney. Identifier ce produit. D’autres métaux peuvent catalyser l’hydrogénation des alcènes : le palladium, le platine… Que signifient les écritures Pd/C, Pd/CaCO3 et Pd/BaSO4 pour le catalyseur ? Le métal paladium finement divisé est déposé sur un support : C ou CaCO3 ou BaSO4. Quelle est l’espèce catalytique pour le catalyseur de Adams PtO2 ? Le platine. Quel est le rôle de la quinoléine dans le catalyseur de Lindlar Pd/CaCO3 ? Citer un exemple d’utilisation de ce catalyseur.  Ce catalyseur est rès sélectif, son activité est diminuée et l'hydrogénation ultérieure de l'alcène en alcane est réduite. Utilisation : hydrogénation des alcynes en alcènes.

menu