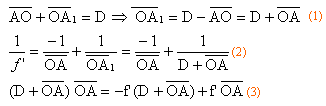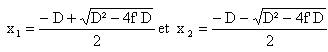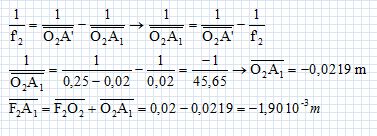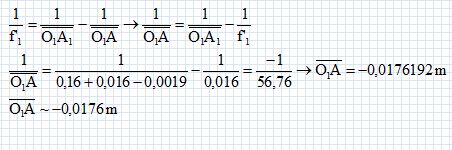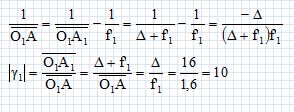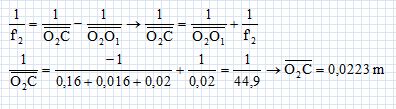Microscopie optique : concours CAPLP maths sciences 2012

Aurélie 14/02/12

Microscopie optique : concours CAPLP maths sciences 2012.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

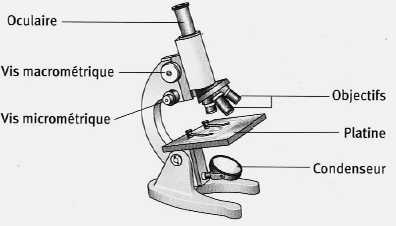
Un microscope est un instrument d'optique destiné à observer d’objets ou détails d'objets dont les dimensions sont de l'ordre du micromètre. Il est constitué de deux systèmes convergents : un objectif et un oculaire.
L'objectif est un système constitué de plusieurs lentilles assimilables à une seule lentille de courte distance focale de l'ordre du millimètre. L'oculaire est équivalent à une loupe de distance focale de l'ordre du centimètre.
La mise au point se fait en déplaçant l'ensemble objectif-oculaire par rapport à l'objet étudié à l'aide de la vis macrométrique pour un réglage grossier puis à l'aide de la vis micrométrique pour un réglage fin.
Le tableau ci-dessous renseigne sur quelques caractéristiques de l'objectif et de l'oculaire d'un microscope utilisé en travaux pratiques avec des élèves.

Objectif L₁ distance focale f'₁ =16 mm
diamètre D₁ =9,0mm
grandissement |g₁| =10
Oculaire L₂ vergence C₂ = + 50 d
grossissement G₂ = 12,5

Généralités en optique géométrique.
Enoncer les conditions de Gauss et définir les termes de stigmatisme rigoureux et d'aplanétisme.
Conditions de Gauss : l'objet doit être de petites dimensions et placé au voisinage de l'axe optique principal du système optique. On élimine ainsi les rayons lumineux trop inclinés sur l'axe optique.
Les systèmes optiques possèdent en général un axe de symétrie appelé axe optique. Soit un point A de cet axe envoyant un faisceau sur l'instrument : à la sortie si le faisceau converge en un point A' situé sur l'axe, on dit que A et A' sont conjugués.
Stigmatisme rigoureux pour un couple de points A et A' conjugués : tous les rayons issus de A passent par A'. Un miroir plan est rigoureusement stigmatique pour tous couples de points (A, A').
Aplanétisme : le stigmatisme doit être rigoureux pour le couple A et A' et le couple B et B' ; B et A se trouvant dans un plan de front.
Décrire une méthode permettant de distinguer les lentilles convergentes des lentilles divergentes.
Au toucher, une lentille convergente est plus épaisse au centre que sur les bords ; une lentille divergente est plus épaisse sur les bords qu'au centre.
Caractériser une lentille mince et définir sa vergence.
Milieu homogène, isotrope, transparent : au moins l'un des dioptres n'est pas plan.
Mince : l'épaisseur de la lentille doit être faible par rapport aux rayons de courbure de chaque dioptre.
La vergence, exprimée en dioptrie, est l'inverse de la distance focale image, exprimée en mètre.
Rappeler, sans démonstration, pour les lentilles minces les formules de conjugaison et de grandissement avec origine au centre optique.

Définir l'indice de réfraction d'un milieu. Donner les valeurs des indices de réfraction du vide n_vide, de l'air n_air et de deux autres milieux.
L'indice de réfraction d'un milieu transparent, à une longueur d'onde donnée, est le rapport de la célérité de la lumière dans le vide à la célérité de la lumière dans le milieu ; n_vide = 1,00 ; n_air =1,000277 ; n_eau = 1,33 ; n_verre = 1,5.
Dans la pratique scolaire n_air = 1,0.
La valeur de n_air est-elle constante ou bien dépend-elle de paramètre(s) que l'on prévisera ?
n_air dépend de la température, de la pression, de la masse volumique de l'air.
Définir un milieu dispersif. Citer un exemple de milieu dispersif et une manifestation concrète de la dispersion de la lumière.
Dans un milieu dispersif, la célérité de la lumière dépend de la fréquence.
Un prisme de verre est un milieu dispersif pour la lumière blanche : on observe à la sortie du prisme un spectre d'émission continu contenant toutes les couleurs de l'arc en ciel.

Etude de l'objectif du microscope.
L’objectif du microscope utilisé par les élèves est assimilé à une lentille L₁ plan convexe en verre, d’indice de réfraction n. L’indice de l’air entourant la lentille est pris égal à 1,00.
Le dioptre d’entrée de la lentille L₁ est plan. Le dioptre de sortie est sphérique, de rayon R = CS = 8,32 mm avec C, le centre du dioptre sphérique et S, le point de concours du dioptre sphérique avec l’axe optique.
Le centre optique O₁ de la lentille est le point de concours du dioptre plan avec l’axe optique. L’épaisseur de la lentille, e = O₁S = 1,35 mm, est inférieure au rayon R du dioptre de sortie.
Un faisceau lumineux incident, assimilé à un rayon de lumière lumière, arrive parallèlement à l’axe optique sur le dioptre plan en un point A. Ce rayon et l’axe optique sont séparés d’une distance h = 1,00 mm. Le schéma ci-dessous est réalisé sans souci d’échelle.
Le faisceau lumineux incident est monochromatique.
Reproduire sur la copie le schéma ci-dessus puis tracer sans souci d’échelle la marche d’un faisceau monochromatique incident traversant la lentille et réfracté au point B où le rayon arrive sur le dioptre sphérique. Faire figurer les angles d’incidence i et de réfraction r au point B.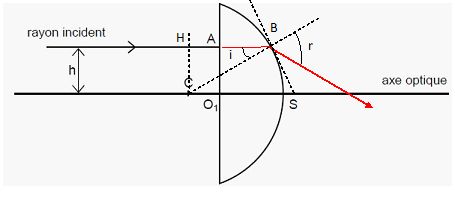

Montrer que l’angle d’incidence i au point B s’écrit : i = sin^-1(h/ R).
Dans le triangle rectangle CHB : sin i = h / CB = h / R ; i = sin^-1(h/ R).
Exprimer l’angle de réfraction r en fonction de n, n_air, h et R.
n sin i = n_air sin r ; sin r = n / n_air sin i ; r = sin^-1( n / n_air sin i).
Discuter suivant les valeurs de l’angle d’incidence i, les trajets possibles du rayon incident au point B pour un indice de réfraction moyen de valeur n = 1,52.
La plus grande valeur possible de sin r est 1. Il existe un angle d'incidence limite i_lim au delà duquel la réfraction ne se produit plus.
i_lim = sin^-1(n/n_air) = 41,1°.
Il y a réfraction en B si l'angle d'incidence i est inférieur ou égal à i_lim. Il y à réflexion totale en B si i est supérieur à i_lim.
On considère que le faisceau lumineux incident est constitué de deux radiations de longueurs d’onde dans le vide l₁ = 450 nm et l₂ = 650 nm. Les indices de réfraction du verre correspondant aux longueurs d’onde l₁ et l₂ sont respectivement n₁ = 1,53 et n₂ = 1,51.
Justifier la différence entre les valeurs des indices n₁ et n₂.
Le verre est un milieu dispersif pour une lumière polychromatique.
Préciser les couleurs des radiations de longueurs d’onde l₁ et l₂. Calculer les valeurs des angles de réfraction r₁ et r₂ respectifs. Qu’observe-t-on à la sortie de la lentille ? Quel type de défaut optique de la lentille étudiée est ainsi mis en évidence ?
450 nm : indigo ; 650 nm : rouge.
i = sin^-1(1,00/ 8,32) =6,90° ; r₁ = sin^-1((n/n_air sin i) =sin^-1((1,53 sin 6,90) = 10,6°.
r₂ = sin^-1((n/n_air sin i) =sin^-1((1,51 sin 6,90) = 10,5°.
L'indigo est plus dévié que le rouge : le principal défaut d'une lentille est appelé défaut d'aberrations chromatiques ; l'image d'un point est une petite tache irrisée de rouge ou de bleu.
L’objectif d’un microscope est souvent constitué d’une succession de lentilles accolées ayant des verres de pouvoirs dispersifs différents afin d’obtenir un objectif achromatique. Expliquer ce dernier terme.
Ces objectifs sont corrigés pour le rouge et le bleu : ils ne présentent pas d'aberrations chromatiques.
Pour une valeur moyenne de l’indice de réfraction n = 1,52, déterminer le diamètre minimum D_max de la lentille permettant d’éviter le phénomène de réflexion totale. Ce phénomène peut-il se produire avec la lentille L₁ ?
L'angle d'incidence limite i_lim en B permettant d'éviter la réflexion totale est tel que : sin i_lim = 1/n = 1/1,52 = 0,658.
L'angle d'incidence en B doit être inférieur à i_lim pour éviter la réflexion totale.
Or sin i_lim =h / CB ; CB = h / sin i_lim = 1,00 / 0,658 = 1,52 mm. D_min > 2 CB = 3,04 mm.
Ce phénomène de réflexion totale ne peut pas se produire avec la lentille L₁ car son diamètre est égal à 2*8,32 = 16,6 mm, valeur bien supérieure à 3,04 mm.
On considère à nouveau que la lentille L₁ a un indice de réfraction moyen de valeur n = 1,52.
En utilisant le schéma réalisé, nommer le point d’intersection du rayon réfracté avec l’axe optique.
Un rayon incident parallèle à l'axe optique principal émerge en passant par le foyer principal image de la lentille.
Montrer que la distance L séparant le centre optique O₁ et ce point peut se mettre sous la forme : L =R (cos i-1) + e + h / tan (r-i).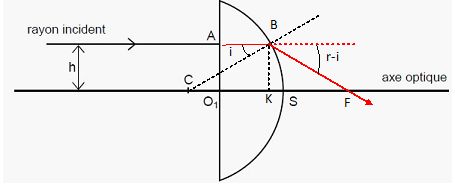

L = O₁K + KF = O₁S -KS + KF = O₁S -( CS-CK) + KF = e - R+R cos i +h / (tan(r-i)).
Calculer la valeur de L pour h = 1,00 mm puis h = 2,50 mm. Quel type de défaut optique de la lentille est ainsi mis en évidence ?
h = 1,00 mm : i = sin^-1(h/ R)= i = sin^-1(1,00 / 8,32 )=6,903 ) ; cos i =0,993.
r = sin^-1( n / n_air sin i)= sin^-1( 1,52 sin 6,903)=10,5° ; L = 8,32 ( 0,993 -1) +1,35 +1,00 / tan (10,5-6,90)= -0,0582 +1,35 + 15,77 ~17,1 mm.
h = 2,50 mm : i = sin^-1(h/ R)= i = sin^-1(2,50 / 8,32 )=17,49 ) ; cos i =0,954.
r = sin^-1( n / n_air sin i)= sin^-1( 1,52 sin 17,49)=27,18° ; L = 8,32 ( 0,954 -1) +1,35 +2,50 / tan (27,18-17,49)= -0,383 +1,35 + 14,64 ~15,6 mm.
L'aberration sphérique : les rayons provenant du bord et du centre de l'optique ne focalisent plus au même point.
Si la lentille est supposée mince et utilisée dans les conditions de Gauss, montrer, en faisant les approximations appropriées, que la distance L s’écrit : L ≈ R /(n-1).
En utilisant cette relation, discuter les conditions de stigmatisme d’une lentille mince.
tan(r-i) ~ r-i en radian ; cos i -1 ~ 0 ; r ~ n i ; r-i ~(n-1) i ; L ~ e + h / ( (n-1) i).
Or sin i ~ i ~ h / R d'où L ~ e + R / (n-1).
Si la lentille est supposée mince, e est négligeable devant R/(n-1).
Les lentilles minces sphériques donnent d'un point A une image unique que dans les conditions de Gauss : les rayons lumineux sont proches de l'axe et peu inclinés par rapport à l'axe.

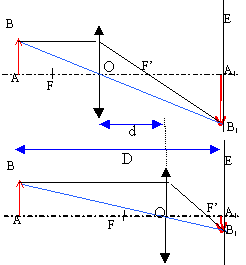
Dans la suite, toute lentille mince sera supposée rigoureusement stigmatique quelle que soit la position de l’objet.
Étude de l’oculaire du microscope.
L'oculaire du microscope étudié est assimilé à une lentille mince convergente L₂ de distance focale f’ étudiée a priori dans les conditions de Gauss.
Afin de déterminer la distance focale f’ de l’oculaire, un objet lumineux AB perpendiculaire à l’axe optique de la lentille L₂ est positionné à la graduation zéro sur un banc optique. L’écran fixe est placé à une distance D supérieure à 4f’ de l’objet.
Montrer qu’il existe sur le banc optique, deux positions O_2a et O_2b du centre optique de la lentille pour lesquelles l’image A’B’ de l’objet AB est nette sur l’écran.
La distance séparant les deux positions O2a et O2b précédentes est notée d.
Déterminer l’expression de f’ en fonction de d et D. En déduire la valeur de f’ sachant que D = 20,0 cm et d = 15,5 cm.

(2) réduction au même dénominateur. Les dénominateurs étant égaux, il y a égalité entre les numérateurs. On pose mesure algébrique de OA = x.
d'où en effectuant : D x +x² = -f' D -f' x + f' x.
x² + Dx + f'D=0
résoudre l'équation du second degré : D= D²-4f'D ; le discriminant est positif si D >4f'.

La différence x₁-x₂ est égale à d. Elever au carré d'où : d² = D²-4f'D, soit (D²-d²) / (4D) = f'
f' = (0,2²-0,155²) / 0,8 ~0,0200m ~2,00 cm.

La lentille L₂ est maintenant utilisée comme une loupe.
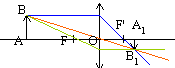
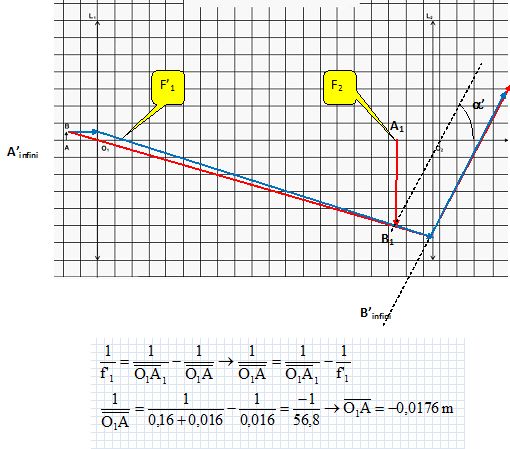
Lorsque l’objet AB est placé à 1,5 cm de la lentille L₂, utilisée comme une loupe, son image est située à 6,0 cm de L₂.
Déterminer par un tracé, la position des foyers principaux objet et image de L₂ et positionner l’image A’B’. Retrouver la valeur de f’ à partir de la construction géométrique.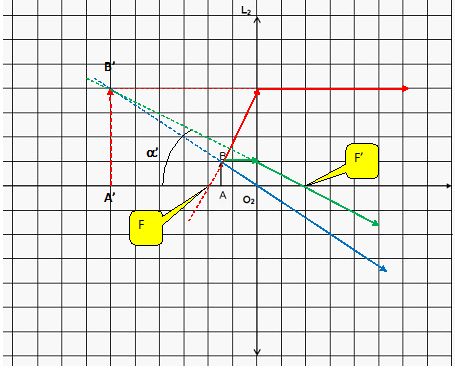

La puissance P d’une loupe et son grossissement G sont définis par les relations : P = α’ / AB et G = α’/α, avec :
α’ : l’angle sous lequel est vue l’image A’B’ donnée par la loupe.
α : le diamètre apparent de l’objet, c’est l'angle de vision directe à l'oeil nu de l'objet placé à la distance d_m = 25,0 cm de l’oeil.
Exprimer puis calculer la puissance P et le grossissement G de la lentille L₂utilisée comme une loupe lorsque l’oeil de l’observateur est placé au foyer image F’ de la lentille L₂. On supposera que tanα’ ≈ α’.
Le grandissement transversal est égal à : O₂A'/O₂A =A'B' / AB = 6/1,5 = 4 ; tan a' ~a'= A'B' / A'F'= 4 AB /0,08. P = 4/0,08 = 50 m^-1.
tan a ~ a = AB / d_m =AB / 0,25 = 4 AB ; G = 12,5 m^-1 ou dioptries.

Afin d'obtenir un grossissement supérieur à celui d'une loupe, on utilise souvent un microscope.
Réalisation d'un microscope réduit.
Le microscope réduit comprend les deux lentilles précédentes utilisées dans les conditions de Gauss.
L'objectif L₁ est une lentille mince de distance focale f'₁=16 mm et de diamètre D₁ = 9,0 mm. L'intervalle optique D représente la distance entre le foyer image de l'objectif et le foyer objet de l'oculaire, il est fixe et a pour valeur normalisée D = 16,0 cm. L'oculaire L₂ est une lentille mince de vergence 50 dioptries.
L'observateur a une vision normale, il regarde à travers le microscope un objet AB sans accommoder, l'image définitive A'B' est donc située à l'infini.
Où se situé l'image intermédiaire A₁B₁ ?
L'image intermédiaire, objet pour l'oculaire, se situe au foyer objet de l'oculaire.
Déterminer la valeur de la grandeur algébrique O₁A permettant de positionner l'objet AB par rapport à l'objectif L₁.

L'observateur dont l'oeil est placé au foyer principal image de l'oculaire accommode à présent au maximum : l'image définitive est située à d_m = 25 cm de l'oeil, d_m étant la distance minimale de vision distincte.
Déterminer la position de l'image intermédiaire A₁B₁ par rapport au foyer objet de l'oculaire L₂.

Déterminer la valeur de la grandeur algébrique O₁A permettant de situer la nouvelle position l'objet AB par rapport à l'objectif L₁.

Déterminer la latitude de mise au point. Expliquer la présence d'une vis micrométrique sur le microscope.
0,0176192-0,0176 = 1,92 10^-5 m~19 µm.
La mise au point ( 19 µm ) doit être réalisée avec un dispositif permettant de modifier très lentement la distance objectif-objet. La vis micrométrique le permet.
Le grossissement G est défini par la relation : G = α’/α, avec :
α’ : l’angle sous lequel est vue l’image A’B’ formée à l'infini.
α : le diamètre apparent de l’objet, c’est l'angle de vision directe à l'oeil nu de l'objet placé à la distance d_m = 25,0 cm de l’oeil.
Exprimer la valeur absolue du grandissement de l'objectif notée |g₁| en fonction de D et f'₁. Calculer |g₁|.

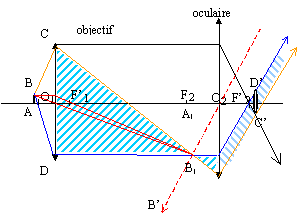
Exprimer puis calculer le grossissement du microscope en fonction de |g₁| et du grossissement G₂ de l'oculaire.
G = a'/a ; tan a' ~a' = A₁B₁ / f'₂ ; tan a ~a = AB / d_m ; G = A₁B₁ / AB *d_m/ f'₂=|g₁| *d_m/ f'₂=|g₁| G₂.
G = 10 *0,25 / 0,02 =125.
L'observateur place son oeil dans le plan du cercle oculaire du microscope.
Donner la définition du cercle oculaire.
Le cercle oculaire ( C'D' figure ci-dessous) d'un instrument d'optique est l'image de l'objectif à travers l'oculaire.
Déterminer la position du cercle oculaire par rapport à l'oculaire. Quel est l'intérêt de connaître ce paramètre ?

Tous les rayons qui entrent dans le microscope par l'objectif sortent donc par le cercle oculaire.
On doit placer la pupille de l'œil dans ce cercle afin qu'un maximum de lumière entre dans le récepteur, l'oeil.

menu