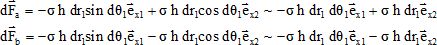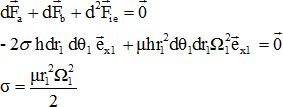Sur
un Compact-disc, les informations sont stockées sous forme de "creux"
et de "plats" le long d'une piste métallique réfléchissante en forme de
spirale. Celle-ci démarre à une distance R1 = 2,50 cm de l'axe du CD, et se termine à R2 = 5,80 cm.
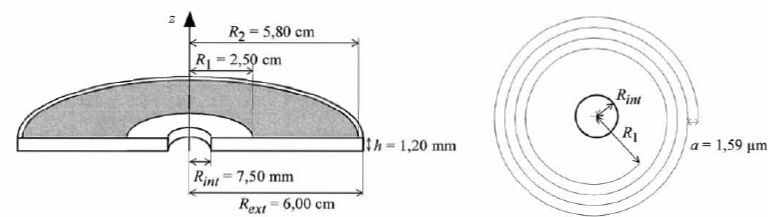
La zone grisée correspond à la portion du CD occupée par la piste
métallique, la partie blanche est le substrat en polycarbonate. Les
spécifications du CD recommandent une vitesse de lecture linéaire v0 = 1,22 m/s et un pas de spirale a = 1,59 µm. On peut noter que a << R1.
|
|
Etude de la piste du CD.
Etablir
l'expression littérale de la "surface utile " S du CD, c'est à dire la
surface grisée sur laquelle s'étend la piste en spirale.
S = p R22 - p R12 = p(R22-R12).
Donner
sans démonstration, une estimation de la longueur totale L de la piste
en fonction de S et a. Calculer sa valeur numérique.
L~S / a ~ p(R22-R12) / a = 3,14 ( 5,802-2,502 )10-4 / 1,59 10-6 =5411,8 ~5,41 103 m.
Quelle valeur numérique de la durée de lecture Dt exprimée en minutes, cela représente t-il ?
Dt = L/ v0 = 5411,8 / 1,22 = 4436 s = 73,9 min.
Un disque de concertos de Bach totalement gravé offre effectivement 74 minutes d’écoute.
Etablir l'expression de la vitesse angulaire W(r) de rotation que doit avoir li disque lorsque la tête de lecture est à la distance r de l'axe de rotation.
W(r) = v0 / r.
Dans l'intervalle [R1 ; R2 ] pour quelle valeur de r la fonction W(r) est-elle maximale ?
W(r) est maximale pour la plus petite valeur de r, soit r = R1.
Calculer Wmax.
Wmax= v0 /R1 = 1,22 / 2,50 10-2 = 48,8 rad /s ~7,77 tours/s ~466 tours/min.
Les lecteurs de CD-ROM ont des vitesses de lecture beaucoup plus
importantes que celles des lecteurs de CD audio. Un lecteur dit "52 X"
a ainsi une vitesse de lecture linéaire égale à 52 v0.
Calculer W'max.
W'max = 52v0 /R1 =52 Wmax=52*466 =2,42 104 tours/min.
Les différents modes de lecture.
Pour éviter les difficultés engendrées par de très grandes vitesses de
rotation angulaires, certains lecteurs CD ont un mode de fonctionnement
différent : ils assurent une vitesse angulaire constante ( mode CAV )
pour le début de la spirale puis une vitesse linéaire constante ( mode
CLV) pour le reste.
Supposons par exemple que la vitesse angulaire soit constante ( mode CAV, W = W0 ) lorsque l'éloignement entre l'axe de rotation et la tête de lecture est compris entre R1 et R3 =4,50 cm ; puis que sa vitesse linéaire de défilement de la piste devant la tête de lecture soit constante et égale à 52 v0 entre R3 et R2.
Donner l'expression littérale de W0 en fonction des paramètres jugés
nécessaires, pour traduire la continuité de la vitesse linéaire de lecture lors du passage du mode CAV au mode CLV.
La continuité de la vitesse linéaire à la distance R3 de l'axe s'écrit : W0 R3 =52 v0 ; W0 =52 v0 / R3.
|
En mode CAV à W0 la vitesse linéaire de lecture est une fonction de l'éloignement r entre l'axe de rotation et la tête de lecture.
Donner l'expression littérale de v(r).
v(r) = W0 r.
On note N1 le nombre de tours que doit faire le disque pendant toute la durée de la phase CAV.
Exprimer N1 en fonction de R1, R3 et a.
Initialement la tête de lecture se trouve à la distance R1 de l'axe ; au bout d'un tour, elle se trouve à la distance R1+a de l'axe; au bout de deux tours, elle se trouve à la distance R1+2a de l'axe ; au bout de N1 tours, elle se trouve à la distance R1+N1 a = R3. N1 = (R3-R1) /a =(4,5 -2,5) 10-2 / 1,59 10-6 = 1,2579 104 ~1,26 104 tours.
Déterminer la durée totale Dt1 de la lecture en mode CAV de la portion de piste comprise entre R1 et R3.
Une expression de Dt1 en fonction de R1, R3, a et v0 est attendue.
Dt1 =2p N1 / W0 = 2p R3 (R3-R1) /(52 a v0) =2*3,14 *4,5 10-2 *(4,5 -2,5) 10-2 / ( 52 *1,59 10-6 *1,22) = 56,06 ~56,1 s.
Déterminer la durée totale Dt2 de la lecture en mode CLV de la portion de piste comprise entre R3 et R2.
Une expression de Dt2 en fonction de R2, R3, a et v0 est attendue.
Estimation de la longueur L'' de la piste :
L''~S'' / a ~ p(R22-R32) / a.
Dt2 = L'' / (52v0) =p(R22-R32) / (52 v0 a ) = 3,14(5,802-4,502) 10-4 / (52*1,22*1,59 10-6) = 41,7 s.
Quelle est en minutes, la durée totale Dt' de la lecture de ce disque ?
Dt' =Dt1 + Dt2 =56,1 +41,7 =97,8 s ~1 min 38 s.
Mécanique dans un référentiel non galiléen.

Un lecteur de CD-ROM est fixé sur une table. On suppose que le référentiel R0
lié à la table est galiléen. On lui associe un repère orthonormé direct
( O, x, y, z). A l'intérieur du lecteur, un dispositif d'entraînement
communique au CD-ROM un mouvement de rotation autour de l'axe Oz,
vertical ascendant. La vitesse angulaire est notée W. Dans cette question, le CD-ROM est modélisé par un cylindre homogène en polycarbonate de hauteur h = 1,20 mm, de rayon Rext = 6,00 cm, percé en son centre d'un trou circulaire de rayon Rint = 7,50 mm. Sa masse volumique est µ =1,20 103 kg m-3. Soit R1 le référentiel lié au disque. On lui associe un repère orthonormé direct ( O, x1, y1, z1), l'axe Oz1 étant confondu avec l'axe Oz. On note 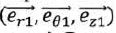 la base vectorielle des coordonnées cylindriques permettant de repérer un point dans R1. Dans le cas où R1 est animé d'un mouvement de rotation uniforme par rapport à R0 autour de l'axe Oz, on admet que l'accélértion d'inertie d'entraînement d'un point M s'écrit : la base vectorielle des coordonnées cylindriques permettant de repérer un point dans R1. Dans le cas où R1 est animé d'un mouvement de rotation uniforme par rapport à R0 autour de l'axe Oz, on admet que l'accélértion d'inertie d'entraînement d'un point M s'écrit :
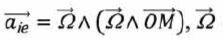 étant le vecteur rotation de R1 par rapport à R0. étant le vecteur rotation de R1 par rapport à R0.
Donner la définition d'un référentiel galiléen.
référentiel galiléen : dans ce référentiel le principe
d'inertie ou 1ère loi de Newton s'applique " un point matériel
pseudo-isolé demeure dans son état de repos ou de mouvement rectiligne
uniforme".
Galileo Galilei, dit galilée ( 1564 - 1642), était un physicien et astronome italien.
Donner succinctement, deux éléments du contenu de son travail scientifique.
Il perfectionne la lunette astronomique ; il est un défenseur de l'héliocentrisme.
On conduit l'étude dans le référentiel R1 lié au disque. La vitesse angulaire est constante au cours du temps : W = W1. On considère un point matériel M de masse m fixe dans R1, repéré par ces coordonnées cylindriques ( r1, q1, z1). Exprimer la force d'inertie d'entraînement à laquelle est soumis le point M.
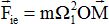
Résistance mécanique des disques optiques numériques.
On se place dans le référentiel R1. Afin d'étudier les forces qui assurent la cohésion d'un CD-ROM en rotation uniforme à la vitesse angulaire W1, considéron une portion de disque dont la distance à l'axe de rotation s'étend de r1 à r1+dr1.
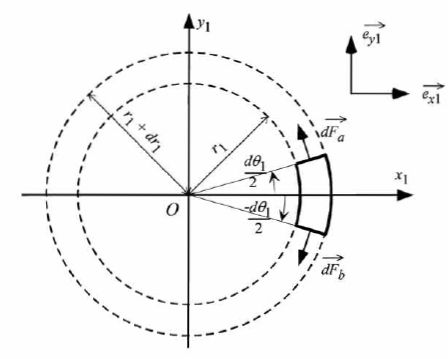
Au sein de cette couronne circulaire, isolons un élément de largeur angulaire élémentaire dq1, situé dans le domaine [-½dq1 ; ½dq1 ].
Quelle est l'expression de la masse d2m de cet élément de CD-ROM d'épaisseur h ?
d2m = µ r1dq1 dr1 h.
Quelle est dans la base 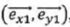 l'expression de la force d'inertie d'entraînement qui s'exerce sur cet élément ? l'expression de la force d'inertie d'entraînement qui s'exerce sur cet élément ?
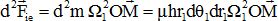
On note 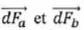 les forces exercées sur l'élément considéré par les deux secteurs angulaires voisins. Soit s la contrainte ( force normale par unité de surface ) à l'interface entre les deux éléments de la portion de disque. les forces exercées sur l'élément considéré par les deux secteurs angulaires voisins. Soit s la contrainte ( force normale par unité de surface ) à l'interface entre les deux éléments de la portion de disque.
dFa = dFb = sdS avec dS = h dr1, surface rectangulaire de séparation.
Donner les expressions vectorielles approchées de ces forces en se limitant à l'ordre 1 par rapport à dq1.
dq1 étant petit sin dq1 ~dq1 et cos dq1 ~1.
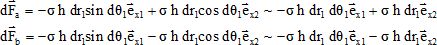
En écrivant l'équilibre dans R1 de l'élément de masse d2m, exprimer s en fonction de µ, r1 et W1.
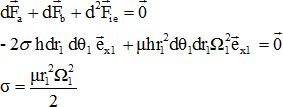
Pour quelle valeur de r1 appartenant à [Rint ; Rext ] la contrainte est-elle maximale ?
La contrainte est maximale pour la plus grande valeur de r1 soit r1 = Rext.
On donne srup =65,0 MPa. Exprimer puis calculer numériquement W1max à partir de laquelle le disque risque de se briser.
W1max =(2 srup /µ)½/ Rext =(2*65,0 106 /1,20 103)½ / 6,00 10-2 =5,5 103 rad/s ~5,2 104 tours/min.
Ce calcul ne donne qu'un ordre de grandeur, dans la mesure où il ne
prend pas en compte les interactions entre les différentes couronnes.
|
|


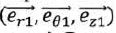 la base vectorielle des coordonnées cylindriques permettant de repérer un point dans R1. Dans le cas où R1 est animé d'un mouvement de rotation uniforme par rapport à R0 autour de l'axe Oz, on admet que l'accélértion d'inertie d'entraînement d'un point M s'écrit :
la base vectorielle des coordonnées cylindriques permettant de repérer un point dans R1. Dans le cas où R1 est animé d'un mouvement de rotation uniforme par rapport à R0 autour de l'axe Oz, on admet que l'accélértion d'inertie d'entraînement d'un point M s'écrit :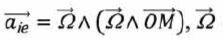 étant le vecteur rotation de R1 par rapport à R0.
étant le vecteur rotation de R1 par rapport à R0.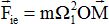

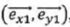
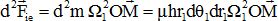
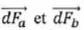 les forces exercées sur l'élément considéré par les deux secteurs angulaires voisins. Soit
les forces exercées sur l'élément considéré par les deux secteurs angulaires voisins. Soit