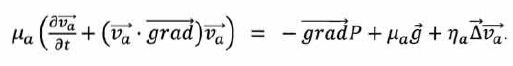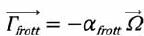|
Mise en rotation du disque et frottements, écoulement de Couette plan : concours Capes 2012. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||
| .
. |
||||||
|
||||||

vx(z) = A z + B avec A et B des constantes d'intégration. Zone ½h+h' > z > ½h : vx(½h+h') =0 = A (½h+h') + B (1) ; vx(½h) =vp0= A (½h) + B (2). (1)-(2) donne : A (½h+h')-A (½h) = -vp0 ; Ah' = -vp0 ; A = - vp0/ h' ; B = vp0/ h' (½h+h'). vx+(z) = - vp0/ h' z +vp0/ h' (½h+h') = vp0/ h'(-z + ½h+h'). Zone -(½h+h') < z < -½h : vx(-½h-h') =0 = -A (½h+h') + B (3) ; vx(-½h) =vp0= -A (½h) + B (4). (3)-(4) donne : -A (½h+h')+A (½h) = -vp0 ; Ah' = -vp0 ; A = vp0/ h' ; B = vp0/ h' (½h+h'). vx-(z) = vp0/ h' z +vp0/ h' (½h+h') = vp0/ h' (z + ½h+h'). On considère une surface élémentaire d2S = dxdy de la partie supérieure ( en z = ½h) de la plaqque mobile. Les vecteurs sont écrits en gras et en bleu. Quelle est la force élémentaire de frottement d2F+ exercée par l'air sur cet élément de surface ? d2F+ = ha dxdy dvx+(z) /dz ex= -ha dxdy vp0/ h' ex. Quelle est la force élémentaire de frottement d2F- exercée par l'air sur un élément de surface situé à la partie inférieure de la plaque ? d2F- = ha dxdy dvx+(z) /dz ex = ha dxdy vp0/ h' ex.
Considérons à présent le lecteur de disques optiques numériques schématisé ci-dessous : 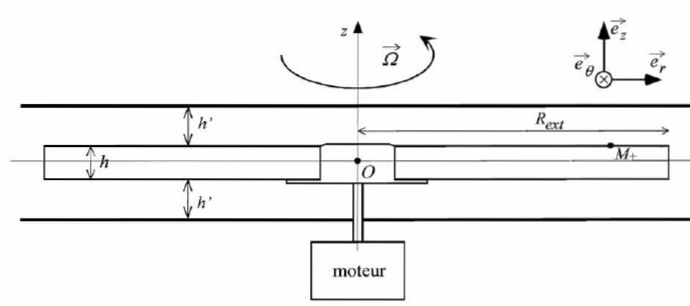 Le référentiel d'étude est R0, lié au boitier de lecture. Il est supposé galiléen. Le disque de hauteur h et de rayon Rext = 6,00 cm est animé d'une vitesse angulaire constante 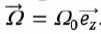 . L'air est considéré comme un fluide newtonien. . L'air est considéré comme un fluide newtonien.Déterminer la vitesse 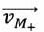 d'un point M+, de coordonnées cylindriques (r, q, ½h) appartenant à la face supérieure du disque. d'un point M+, de coordonnées cylindriques (r, q, ½h) appartenant à la face supérieure du disque.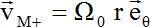 Dans un modèle très simplifié, le champ des vitesses dans l'air peut être considéré comme stationnaire et s'écrire ici sous la forme 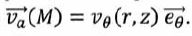 . .En utilisant le résultat ci-dessus et en étant très attentif à la nouvelle géométrie du système, évaluer la force élémentaire de frottement exercée par l'air sur un élément de surface d2S = rdrdq de la partie supérieure du disque, située à une distance r de l'axe de rotation. d2F+ = ha rdrdq dvM+(z) /dz eq= - ha rdrdq W0 r/h' eq= - ha r2drdq W0 / h'eq. F+ = -ha R3ext /3 2 p W0 / h'eq.
|
||||||
|
|
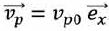 . On donne vp0 = 5,00 m/s.
. On donne vp0 = 5,00 m/s.