Déviation d'un rayon lumineux par un prisme : concours Capes  2012. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

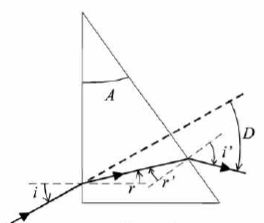
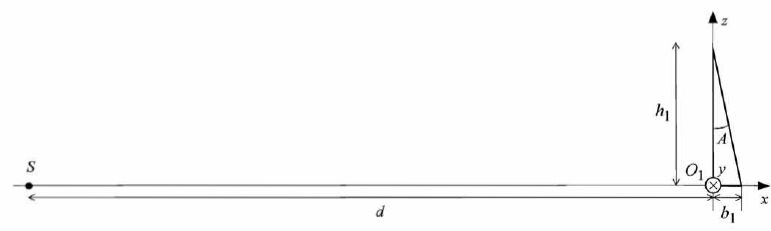
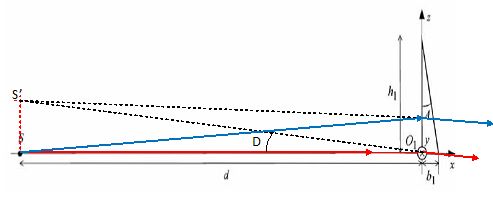
Déviation d'un rayon lumineux par un prisme. Un prisme d'indice n, d'angle au sommet A est représenté ci-dessous. Rappeler les lois de Snell-Descartes reliant i et i' à r et r'. sin i = n sin r ; sin i' = n sin r'. Etablir le lien entre A, r et r'. A = r + r'. Exprimer la déviation D en donction de i, i' et A. D = i-r + i'-r' = i + i' -A. Dans le cadre de l'approximation des petits angles, établir que D = (n-1)A. i ~n r ; i' ~n r' ; D = n r + n r' -A = n(r + r')-A = nA-A = (n-1)A. Un prisme rectangle, de petit angle A, est disposé suivant la figure : Une source lumineuse ponctuelle S a pour coordonnées (-d, 0) dans le plan xO1z. On suppose que d>>h1>>b1. On admet avec un stigmatisme approché, S donne à travers le prisme une image S', qui a pour coordonnées (-d, z0) dans le plan xO1z, avec z0>0. Placer S' en prenant uniquement pour cette question z0 = ½h1 et tracer le parcours de deux rayons lumineux partant de S et traversant le prisme. Montrer que z0 =(n-1)Ad. tan D = z0 / d ~D ( radian) ; or D = (n-1)A d'où z0 =(n-1)Ad. Détection optique d'une erreur de focalisation. Il existe deux techniques couramment utilisées pour détecter un défaut de focalisation du faisceau lumineux sur le disque : l'une fait appel à une lentille astigmatique tandis que l'autre met en oeuvre un double coin prismatique. Nous nous intéresserons à la seconde technique, dont nous allons étudier le principe mais avec un dispositif s'éloignant un peu de celui réellement utilisé, dans un souci de simplification. Ce dispositif est constitué d'une lame semi-réfléchissante, d'une lentille L2, d'un double coin prismatique et d'un ensemble de 4 capteurs lumineux. 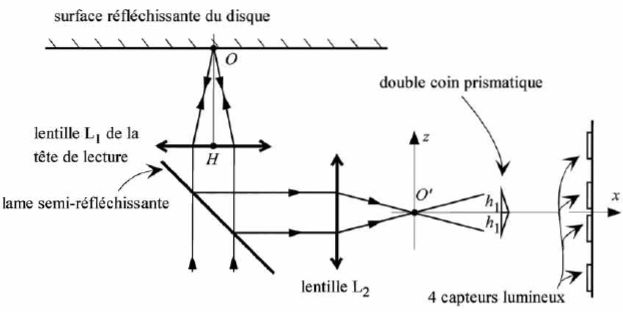Le disque optique est assimilé ici à un miroir plan parfait. La focalisation est bonne lorsque le point O du disque optique est confondu avec le foyer image F'1 de la lentille de lecture L1. A la sortie de la lentille L2, le faisceau converge alors au point O', origine du repère xOz adopté pour cette partie. Supposons qu'une légère perturbation entraîne une légère translation du disque vers le bas. Le point O se trouve ainsi sous F'1. On note N le nouveau point de convergence des rayons après traversée de L2. Où se trouve N par rapport à O' ? Où sont situées les images, notées N' et N", de N à travers le double prisme ? 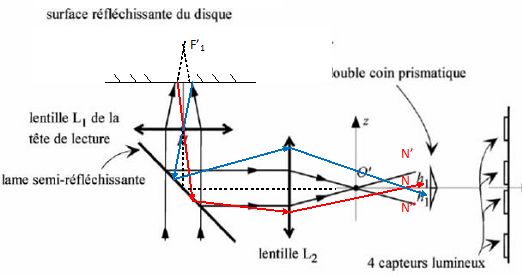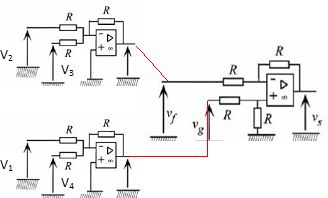Lorsque N est confondu avec O', le faisceau lumineux issu du prisme du haut semble provenir de l'image O'1 de O' à travers le prisme, et recouvre la moitié de chacun des capteurs n°3 et 4, comme le montre la figure. 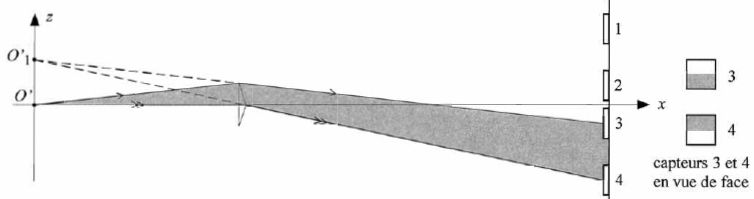Sans calcul et à l'aide d'un schéma représentant les capteurs n°3 et 4 en vue de face, décrire comment sont modifiées leurs zones éclairées ( donc grisées si le point N se trouve sur l'axe O'x légèrement à droite de O'. 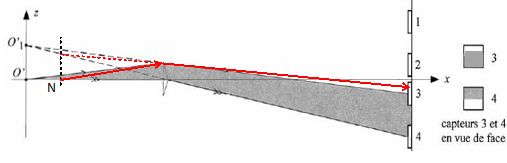Des décalages de N selon les directions des axes O'x et O' z conduisent à des modifications des zones illuminées des 4 capteurs. La partie qui suit donne un exemple de traitement électronique de l'information permettant d'élaborer des signaux d'erreur de position en x et en z  du point N. Dans les conditions de l'expérience, chaque capteur lumineux permet d'obtenir une tension proportionnelle à la surface de sa zone illuminée. le coefficient de proportionnalité est le même pour les 4. Notons vi la tension associée au capteur numéro i. On admet que lorsque tous les rayons lumineux convergent en O' avant de traverser le double coin prismatique, les tension v1 et v2 sont égale à V0 tandis que les tensions v3 et v4 ont pour valeur V'0. Lorsque le point de focalisation n'est pas en O' mais en N, de coordonnées ( x, z ), les tensions sur chaque capteur deviennent : v1 = V0-ßz ; v2 = V0+ax+ßz ; v3 = V'0+ax-ßz ; v4 = V'0+ßz.  a et ß sont des constantes positives. Proposer une combinaison linéaire de ces 4 tensions, donnant un signal proportionnel  à la coordonnée x du point de focalisation, les coefficients de la combinaison linéaire étant indépendants de V0 et V'0. v2-v1 = ax+2ßz ; v3-v4 = ax-2ßz ; v2-v1 +v3-v4 = 2ax. On considère à présent les montages électroniques suivants dans lesquels chaque amplificateur opérationnel est supposé idéal et en fonctionnement linéaire. 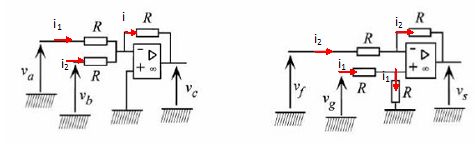Le montage de gauche comporte deux entrées et une sortie. Déterminer son impédance de sortie. Etablir l'expression de Vc en fonction de Va et Vb. L'impédance de sortie est généralement faible de 10 à 500 ohms. Dans notre cas, aucune impédance n'est montée en sortie. Vc = - Ri ; Va =  Ri1 ; Vb =  Ri2 ;  i = i1 + i2 ; -Vc / R = Va / R +Vb / R ; Vc = -(Va+Vb). Montrer que cette relation reste encore valable si un autre circuit est branché entre les deux bornes de sortie du montage de gauche. L'amplificateur étant idéal, les intensités des courants dans les deux entrées sont nuls. Le montage de la figure de droite comporte deux entrées et une sortie. Déterminer son impédance d'entrée pour l'entrée associée à la tension vg. Exprimer vs en fonction de vg et vf. vg = 2 R i1 ; vs +2Ri2 = vf ; R i1 +Ri2 =  vf ; ½vg +½(vf -vs )=  vf ;  vs =(vg -vf ). Proposer un montage permettant d'obtenir une tension proportionnelle à la coordonnée x du point N. .

menu