On
considère un miroir plan rectangulaire de centre O, de largeur b et de
longueur H, disposé dans le plan xOy, le petit côté b étant parallèle à
Oy. On suppose que b << H. On peut se référer à la figure
suivante :
 . .
|
|
L'étude quantitative des phénomènes de diffraction s'appuie sur le principe de Huygens-Fresnel.
Ce principe est-il le fruit d'un travail concerté entre Huygens et Fresnel ?
Non, ils n'ont pas vécu à la même époque.
A. Fresnel ( 1788 - 1827 ; C. Huygens (1629 -1695 ).
Quelle est la contribution de chacun dans la formulation du principe ?
Huygens
: la lumière est composée d'ondes ( modèle ondulatoire ). La lumière se
propage de proche en proche. Chaque élément de surface atteint
par la lumière se comporte comme une source secondaire émettant des
ondelettes sphériques.
Fresnel : expériences sur la diffraction de la lumière, pose les bases de sa théorie « vibratoire » de la lumière.
L'amplitude complexe de la vibration lumineuse en un point est la somme
des amplitudes complexes des vibrations produites par toutes les
sources secondaires.
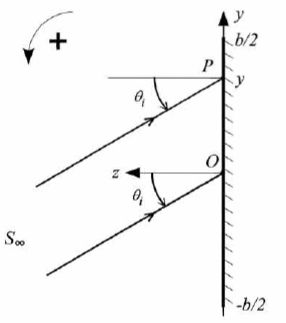
On s'intéresse à la diffraction de Fraunhofer par le miroir rectangulaire. Il est supposé éclairé par une source ponctuelle Soo
située à l'infini. L'onde incidente est donc plane et progressive. Sa
direction de propagation est contenue dans le plan yOz et fait avec
l'axe Oz un angle orienté qi ( compris entre -½p et +½p ). La source Soo est supposée monochromatique, de longueur d'onde dans le vide l1 =589 nm.
Rappeler la définition d'une onde plane.
C'est
une onde dont les fronts d'onde sont des plans infinis, tous
perpendiculaires à une même direction de propagation définie par le
vecteur d'onde, vecteur constant.
Comment peut-on, en pratique, obtenir une onde localement plane et progressive dans une expérience de laboratoire ?
Faire passer de la lumière par un diaphragme puis utiliser une lentille convergente pour la collimater.
Quelle est la couleur de la source de longueur d'onde dans le vide 589 nm ?
Jaune.
On rappelle que les ondes lumineuses visibles correspondent à des longueurs d'ondes dans le vide comprises entre lmin = 400 nm et lmax = 750 nm.
Quelles sont les couleurs associées à chacune de ces longueurs d'onde ?
lmin = 400 nm : violet ; lmax = 750 nm : rouge.
On adopte un modèle scalaire pour la lumière, ainsi que la notation
complexe : la grandeur lumineuse en un point M, associée à une onde
plane progressive monochromatique de pulsation w et de vecteur d'onde k est notée :
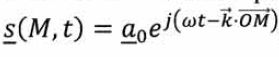
Qu'appelle-t-on le modèle scalaire de la lumière ?
On
associe à une lumière monochromatique, assimilée à une onde plane
progressive, le scalaire amplitude afin de calculer l’intensité
lumineuse. Ce modèle permet d'interpréter
les phénomènes de diffraction et d'interférences : seules les grandeurs
scalaires interviennent, le modèle vectoriel de la lumière n'est pas
fondamental dans ce cas. Les calculs consistent à faire la somme des
amplitudes d'ondes sinusoïdales qui se superposent.
|
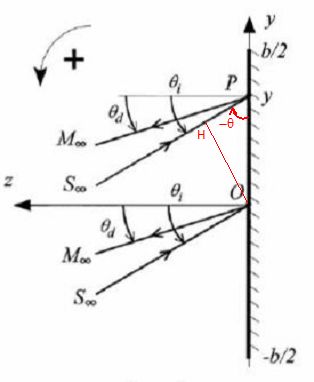
Compte
tenu de la forme très allongée du miroir ( b << H , on restreint
l'étude de l'onde diffractée aux directions de propagation contenues
dans le plan yOz. Grâce à une lunette de visée, on observe la lumière
diffractée an un point Moo, situé à l'infini dans la direction repérée par l'angle orienté qd.
A propos de la lunette.
La lunette de visée est autocollimatrice. Que signifie ce terme ?
C'est une lunette réglée à l'infini : l'oeil observe sans accommoder, sans fatigue.
Décrire en quelques lignes la méthode permettant de la régler pour observer à l'infini.
Eclairer le réticule ; -placer une face réfléchissante verticale,
miroir, sur le plateau ; - régler l'oculaire afin de voir net le
réticule sans accommoder ;
- tourner la seconde bague pour voir nettement à la fois le réticule et son
image par réflexion.
Etude de la différence de chemin optique.
Qu'appelle-ton chemin optique ?
On appelle chemin optique [OM] le produit de la distance OM par l’indice n du milieu.
Exprimer la différence de chemin optique en Moo d =( SooPMoo) - ( SooOMoo) entre le rayon issu de Soo se réfléchissant en P sur le miroir, et celui issu de Soo se réfléchissant en O.
P a pour coordonnées ( 0, y, 0) dans le repère (O, x, y, z). On suppose que l'indice de l'air est égal à 1.
Les rayons incidents sont parallèles, il en est de même des rayons
réfléchis ; l'indice du milieu est égal à 1 : d = -OP sin qi - OP sin qd avec OP = y.
On rappelle que dans le cas du miroir étudié ici l'amplitude complexe de la grandeur lumineuse en Moo peut s'écrire sous la forme intégrale : 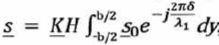
K est une grandeur de dimensionnement ( fixée par les choix de O et de Moo ) et s0 étant l'amplitude complexe de l'onde incidente en O.
En déduire que s peut se mettre sous la forme s = KHbs0 F(p b / l1 (sin qi+sin qd), où F est une fonction à déterminer.
exp [j2p / l1 (sin qi+sin qd) y ] = exp (jAy) en posant A = 2p / l1 (sin qi+sin qd).
Le
sinus cardinal :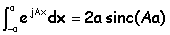
L'intégrale est donc égale à : b s0 sinc(A½b) et s = KHbs0 sinc(A½b) soit F = sinc(A½b) / (½A).
En déduire l'expression de l'éclairement E en Moo.
E = s s*=K K*s0 s0*(HbF(p b / l1 (sin qi+sin qd))2 = K K*s0 s0*(Hb sinc (A½b))2.
On donne le graphe de la fonction F :
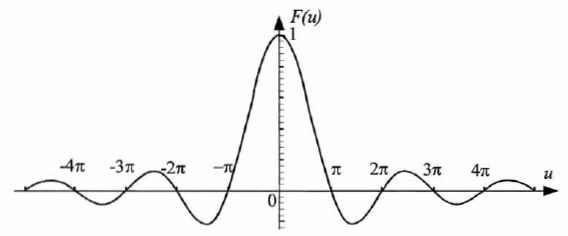 . .
Pour qi =0, exprimer l'ouverture angulaire Dqd du faisceau diffracté correspondant au maximum principal de diffraction.
Cette ouverture angulaire correspond à l'écart entre les deux valeurs ( de signe opposé ) de qd
qui conduisent à la pemmière annulation de l'éclairement. On ne fera
pas l'approximation des petits angles et on supposera b > l1.
E = K K*s0 s0*(Hb sinc (A½b))2 avec A = 2p / l1 sin qd.
Le sinus cardinal est nul pour A½b = k p avec k appartenant à Z*.
2p / l1 ½b sin qd = k p ; b / l1 sin qd = k ; sin qd = k l1 / b.
k = 1 ; sin qd = l1 / b ; k = 1 ; qd = arcsin( l1 / b).
sin qd = - l1 / b ; qd = arcsin( -l1 / b) = -arcsin( l1 / b).
Ecart angulaire : 2arcsin( l1 / b) ~2 l1 / b.
On note emax1 la valeur de l'éclairement pour le maximum principal de diffraction, et emax2 celle correspondant au premier maximum secondaire.
Estimer grahiquement emax2 /emax1.
5 /0,6 ~ 8,3.
|
|
 .
.
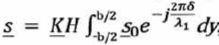
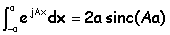

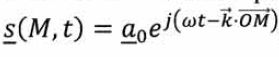
 .
.