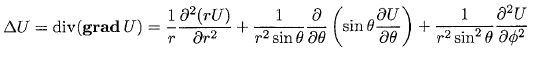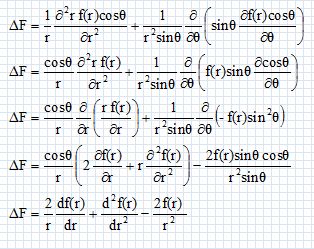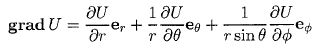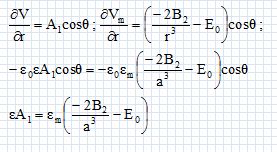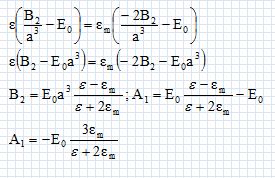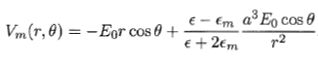
Les grandeurs écrites en gras et en bleu sont des vecteurs.
|
|
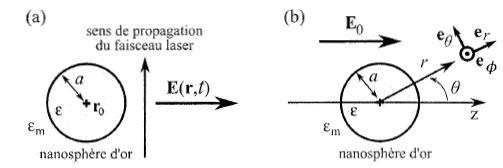
Champ électrique appliqué à la nanosphère.
Au voisinage de la sphère, le champ électrique associé au faisceau laser à la position r peut s'écrire sous la forme :
E(r,t) = EL cos ( k . r-wt) (1) où EL est un vecteur inclus dans le plan de la figure.
Comment se nomment k et w ?
k : vecteur d'onde ; w : pulsation.
Donner la relation liant w à l, puis celle liant la norme de k, w et nm.
w = 2 p f = 2p c / l ; |k| = w nm / c.
Proposer
un argument simple pour justifier que la sphère peut être considérée, à
un instant t donné, plongée dans un champ électrique uniforme E(r0, t), où r0 est la position du centre de la sphère.
a << l : le champ électrique est uniforme au voisinage de la position r0.
Polarisation de la nanosphère dans l'approximation dipolaire.
A un instant t donné, le champ électrique E(r0, t), noté E0, polarise la sphère d'or. Cette polarisation est supposée analogue à celle obtenue en soumettant la sphère à un champ statique E0 = E0 ez, uniforme dans tout l'espace.
Dans cette partie on se place donc dans le cadre de l'électrostatique
afin de déterminer les expressions des potentiels électrostatiques V à
l'intérieur et Vm à l'extérieur de la sphère, sous l'hypothèse
qu'aucune charge libre ne se trouve ni dans le gel, ni dans l'or, ni
dans l'interface gel-or.
Un point de l'espace est repéré à l'aide des coordonnées sphèriques ( r, q, F), le champ E0 déterminant la direction Oz. Montrer que V et Vm sont indépendants de F.
Du fait de la symétrie cylindrique autour de la direction Oz, les potentiels V et Vm sont indépendants de F.
Etablir que V et Vm vérifient l'équation de Laplace : DV = DVm=0.
D représente l'opérateur différentiel Laplacien scalaire.
On utilise les équations de Maxwel dans un diélectrique linéaire isotrope.
Champ électrique statique dans la nanosphère E = -grad V ; l'absence de charge libres se traduit par div E = 0.
div (-grad V) = 0 s'écrit DV =0.
Faire un raisonnement comparable avec Vm.
A grande distance de la sphère, on considère que Vm est le potentiel associé au champ E0ez seul.
En déduire que, pour r >> a, le potentiel Vm( r, q) peut se mettre sous la forme : Vm( r, q) =-E0z = -E0 r cos q.
E0ez = -grad Vm ; seule la composante du gradient suivant z n'est pas nulle, d'où : E0 = - dVm/dz ;
Vm( r, q) =-E0 z + constante. On peut faire le choix d'une constante nulle.
De plus z = r cos q d'où : Vm( r, q) =-E0z = -E0 r cos q.
|
On cherche pour un point quelconque de l'espace, des solutions de l'équation de Laplace DF = 0 de la forme F(r, q) = f(r) cos q.
Montrer que f(r) vérifie l'équation différentielle du second ordre : d2f/dr2 + 2 / r df/dr -2f/r2 = 0. (2)
On rappelle l'expression du Laplacien en coordonnées sphériques :
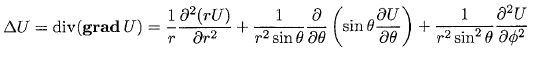
F(r, q) = f(r) cos q ne dépend pas de F, le troisième terme est donc nul.
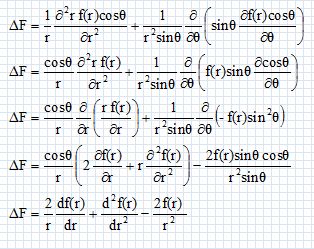
Montrer que l'équation (2) admet des solutions de la forme : f(r) = rm, où m =1 ou m= -2.
Pour m = 1 : df/dr = 1 ; d2f/d2r = 0 par suite : 2/r -2r/r2 = 0 est bien vérifié.
Pour m = -2 : df/dr = -2 r-3 ; d2f/d2r = 6 r-4 par suite : 6 r-4 -4 r-4 -2r-2/r2 = 0 est bien vérifié.
On admet des solutions de la forme F(r,q) = (Ar + Br-2) cos q. A et B sont des constantes réelles.
En déduire que V(r, q) = A1 r cos q et Vm(r, q) =(B2r-2 -E0r) cos q.
Pas de divergence du potentiel V en r=0 ; par suite B =0 et V(r, q) = A1 r cos q.
Pour r >>a : Vm(r, q) = -E0 r cos q ; par suite A = -E0 et Vm(r, q) =(B2r-2 -E0r) cos q.
Afin de déterminer les constantes A1 et B2, on s'interesse à l'interface gel-or.
En écrivant que le potentiel est continu au passage de l'interface, établir une première relation entre A1 et B1.
A1 a cos q = (B2a-2 -E0a) cos q ; A1 = B2a-3 -E0.
Le gel et l'or étant considéré comme des diélectriques linéaires, homogènes et isotropes, on définit les vecteurs D = -e0e grad V dans l'or et Dm = -e0em grad Vm dans le gel.
Déduire de la continuité de la composante radiale de D, une seconde relation entre A1 et B2.
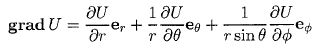
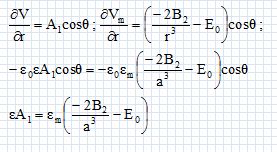
Déterminer A1 et B2.
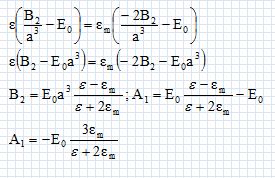
Interpréter ces résultats pour e = em.
B2 = 0 ; A1 = -E0. V(r, q) = -E0 r cos q et Vm(r, q) = -E0 r cos q.
Il s'agit de l'expression du potentiel électrostatique associé à un champ statique uniforme dans un milieu continu.
Montrer que Vm à l'extérieur de la sphère est égal à : 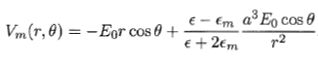
Vm(r, q) =(B2r-2 -E0r) cos q ; remplacer B2r-2 par son expression : E0 a(e-em) / (e+2em).
Le potentiel Vp(r) en un point M(r) situé à grande distance d'un dipôle de moment p placé dans un milieu diélectrique linéaire, homogène et isotrope, de permitivité em, a l'expression suivante :
Vp(r) = 1 /(4 p e0em ) p . r / r3, le dipôle étant placé à l'origine du repère.
Proposer une interprétation physique pour chaque terme de l'expression de Vm(r, q).
Vm(r, q) est la somme de deux potentiels :
- celui associé au champ statique
et celui associé au potentiel créé par un dipôle, centré sur la sphère, d'orientation Oz, de moment p =E0a3 (e-em) / (e+2em) (4 p e0em )ez.
Montrer que le champ électrique E0 induit dans la sphère un dipole p =e0em aE0 avec a =4 p a3 (e-em) / (e+2em).
Identifier p =E0a3 (e-em) / (e+2em) (4 p e0em )ez à p =e0em aE0 pour en déduire a.
|
|