|
|
L'hydrolyse du saccharose en milieu acide n'est pas une transformation rapide.
Etude expérimentale.
A température constante, dans une solution tampon à pH = 5, on mesure
par polarimétrie l'évolution de la concentration du saccharose en
fonction du temps. On obtient les résultats suivants, [S] désignant la
concentration du saccharose.
t (heure)
|
0
|
100
|
250
|
500
|
750
|
1000
|
[S] mol/L
|
0,400
|
0,346
|
0,280
|
0,196
|
0,140
|
0,100
|
| ln([S] / [S]0) |
0
|
-0,145
|
-0,357
|
-0,713
|
-1,05
|
-1,39
|
Cette
transformation est ensuite réalisée à la même température mais avec une
solution tampon à pH = 3,8 ; le temps de demi-réaction est t½ = 31 heures.
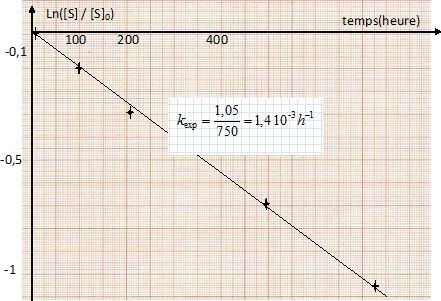
Montrer que la réaction est d'odre 1 par rapport au saccharose et déterminer la valeur de la constante de vitesse apparente kexp.
Dans l'hypothèse d'un ordre 1, on trace la courbe ln([S] / [S]0) en fonction du temps. On doit alors obtenir une droite de coefficient directeur - kexp.
A
l'aide de ces deux expériences, déterminer l'ordre partiel de la
réaction d'hydrolyse du saccharose par rapport aux ions oxonium.
Expérience 1 : t½ = ln2 / k =ln2 / (1,4 10-3) =495 heures.
kexp 1 = k [H3O+]a = k (10-pH)a= k 10-5a =1,4 10-3 (1).
Expérience 2 : kexp 2 = ln2 / t½ =ln2 / 31 =0,0224 h-1 ; kexp 2 = k (10-pH)a= k 10-3,8a =0,0224 (2)
(2) / (1) donne : 101,2a = 0,0224 / (1,4 10-3) ~16 ; 1,2 a = log 16 ; a =1,0.
v = k [S][H3O+].
En déduire la constante de vitesse k.
kexp = k [H3O+] ; k = kexp /[H3O+] = 1,4 10-3 / 10-5 = 1,4 102 L mol-1 h-1.
|
.
.
Mécanisme réactionnel.
Le mécanisme suivant est proposé pour l'hydrolyse du saccharose.

On suppose que les deux réactions de constantes de vitesse ka et k'a sont très rapides de sorte que cet équilibre est toujours atteint quelle que soit la vitesse de consommation de SH+.
Définir un acteélémentaire.
Une réaction se déroulant au niveau des molécules, sans création d'espèces chimiques intermédiaires, est un acte élémentaire.
Peut-on appliquer l'approximation des états quasi-stationnaires à l'espèce SH+ ?
Non :
SH+, réactif de l'étape cinétiquement déterminante ; il n'est pas rapidement consommé.
Exprimer la vitesse correspondant à ce mécanisme et vérifier la cohérence avec les résultats précédents.
v = kb [SH+], l'étape déterminante imposant la vitesse
ka [S][H3O+]=k'a [SH+] ; v = kbka [S][H3O+]/k'a ; on pose k = kbka/k'a. On retrouve bien l'expression précédente.
Influence de la température.
La constante cinétique de la réaction d'hydrolyse suit la loi
d'Arrhénius avec les paramètres suivants : Ea = 108 kJ/mol ; facteur
préexponentiel A = 1,15 1015 mol-1 L s-1.
Evaluer
au bout d'un mois de stockage à 20°C, le pourcentage de saccharose
restant dans la boisson en admettant que le pH de la solution est de 2,5.
ln([S] / [S0] = -kexp t ; [S] /[S0] =exp(-kexp t).
k = A exp(-Ea/(RT) =1,15 1015 exp(-1,08 105 / (8,314 *293)) =6,4 10-5 mol L-1 s-1 ; kexp = k 10-pH =6,4 10-5 *10-2,5 = 2,0 10-7 s-1.
[S] /[S0] =exp(-kexp t) = exp(-2,0 10-7 *30*24*3600) =0,59.
Il reste 59 % du saccharose de départ.
La boisson est soumise à un chauffage à reflux sous agitation. On considère que le saccharose n'est pas initialement hydrolysé.
Evaluer le pourcentage de saccharose hydrolysé au bout d'une demi-heure de reflux.
k = A exp(-Ea/(RT) =1,15 1015 exp(-1,08 105 / (8,314 *373)) =0,863 mol L-1 s-1 ; kexp = k 10-pH =0,863 *10-2,5 = 2,7 10-3 s-1.
[S] /[S0] =exp(-kexp t) = exp(-2,7 10-3 *30*60) =7,8 10-3.
Il reste 0,78 % du saccharose de départ soit 99,2 % de saccharose hydrolysé.
|
|

