|
|
Pour obtenir un faisceau de protons H+ de haute énergie, on utilise un cyclotron constitué de deux demi-cylindres appelés "dees", de rayon Rm
= 15,0 cm à l'interieur desquels règne un champ magnétique
uniforme de valeur B = 2,00 T. Entre les dees, on établit une tension
sinusoïdale u(t) = Umax sin (wt) dont l'amplitude vaut 20,0 kV et où la date t est exprimée en seconde, u(t ) = VD1-VD2 correspond àla différence de potentiel entre les deux dees.
Les
protons sont introduits dans le cyclotron avec une vitesse négligeable
au point O. A cet instant la tension u(t) prend une valeur maximale
positive ou négative. On négligera la durée de transit entre les dees
et le poids de l'ion devant les autres forces.
Donner le signe de u(t) au départ des protons pour qu'ils soient accélérés vers le dee2 D2 pour atteindre le point A.
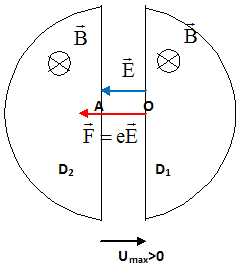
Quelle
est a nature du mouvement des protons entre les deux dees ?
Mouvement rectiligne uniformément accéléré.
Calculer
l'énergie cinétique E1 des protons en A en J et eV.
L'énergie cinétique initiale est voisine de zéro et seule la force électrique travaille:
E1 = e Umax = 20,0 keV ou 1,60 10-19*20,0 103 = 3,20 10-15 J.
En déduire la valeur de la vitesse v1 au point A et en conclure que les prorons sont non relativistes.
½mv12 =E1 ; v1 = (2E1/m)½ = (2*3,2 10-15 /(1,67 10-27))½ =1,96 106 m/s.
Cette valeur est très inférieure à 3 108 m/s : les protons sont non relativistes.
Représenter le champ électrique régnant entre les dees, la vitesse v1 au point A, la force magnétique au point A et la trajectoire des prorons dans le dee.
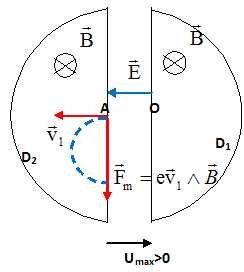
|
.
.
On démontre que le rayon R de la trajectoire empruntée par les protons est donnée par R = m v / (eB).
Quelle est la nature du mouvement des protons à l'intérieur du dee2 ?
Les
protons sont soumis à la seule force magnétique, perpendiculaire à la
vitesse : cette force ne travaille pas et la valeur de la vitesse est
constante.
Le mouvement est uniforme ; de plus R est constant : le mouvement est circulaire.
Donner l'expression de la durée Dt du parcours d'un proton à l'intrieur dun dee. Calculer cette durée.
Le proton de masse m parcourt une demi circonférence de rayon R en Dt seconde : Dt = p R / v1 = p m /(eB).
Dt =3,14 *1,67 10-27 / (1,60 10-19 *2,00) =1,64 10-8 s.
En déduire la valeur de la fréquence f de la tension u(t) de manière à accélérer les protons de manière optimale.
Pour une accélération maximale, à
chaque demi tour, la tension alternative doit changer de
signe et prendre sa valeur maximale.
La demi période de la tension alternative est
égale à la durée d'un demi tour soit T = 2 Dt.
f = 1/T = 1/(2Dt) =3,05 107 Hz.
On considère que les protons sortent lorsque le rayon de leur trajectoire atteint la valeur Rm.
Calculer la valeur de la vitesse vm des protons à leur sortie.
vm = RmeB/m = 0,150*1,6 10-19*2,00 / (1,67 10-27) =2,8743 107 ~2,88 107 m/s.
Calculer l'énergie cinétique Ecm des protons à leur sortie ( J et eV). Les protons sont non relativistes.
Ecm = ½mvm2 = 0,5*1,67 10-27 *(2,8743 107 )2=6,90 10-13 J ou 6,90 10-13 /(1,6 10-19) =4,31 106 eV.
En déduire le nombre N de tours effectués dans le cyclotron.
A chaque demi-tour ( passage entre les dees ) les protons gagnent l'énergie E1.
N = Ecm / (2E1) ~ 108 tours. |
.
|