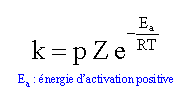|
|
L'élément
nickel.
Donner
la configuration électronique à l’état fondamental de l’atome de nickel.
Z = 28.
1s2 2s2 2p6
3s2 3p6 4s2
3d8.
Le nickel est un élément de transition. Justifier
cette désignation.
"3d8" les orbitales d sont en partie occupées.
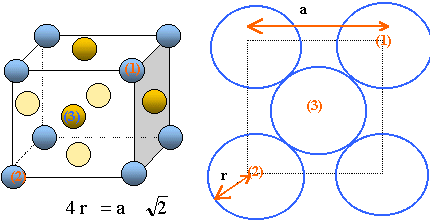
Le nickel cristallise dans une structure cubique à faces centrées
(c.f.c).
Compléter
le schéma de la maille élémentaire.
Établir
la relation littérale liant l’arête a de la maille et le rayon
métallique r du nickel. Calculer la valeur de R. ( a = 360
pm ).
Il
y a contact des sphères suivant la diagonale d'une face du cube.
r= 360 / 4* 1,414 = 127,28 ~ 127 pm.
Établir
l’expression littérale de la masse volumique du nickel et calculer sa
valeur.
La maille compte en propre 4 atomes de nickel ; masse de la maille :
m =4 M(Ni) / NA = 4 *58,7 10-3
/ 6,02 1023 = 3,90 10-25
kg.
Volume de la maille : V=a3 = (3,6 10-10)3
=4,6656 10-29 m3
;
Masse volumique du nickel : m / a = 3,90 10-25
/ (4,6656
10-29)= 8,36 103 kg m-3.
Raffinage
du nickel par le procédé Mond.
Du
nickel de très haute pureté peut être obtenu par réaction entre le
monoxyde de carbone et des pastilles de nickel impur selon la réaction
: Ni(s) + 4 CO(g) = Ni(CO)4 (1)
Aucun autre métal présent dans les pastilles ne réagit dans les mêmes
conditions. Après séparation, Ni(CO)4 est
décomposé selon la réaction inverse pour donner du métal d’une pureté
proche de 99,9 %.
Etude
du complexe Ni(CO)4.
Écrire
le schéma de Lewis de la molécule de monoxyde de carbone. De quelle
molécule CO est–il isoélectronique ?
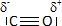 CO est
isoélectronique de N2. CO est
isoélectronique de N2.
Justifier
le caractère de ligand du monoxyde de carbone. Quel type de liaison est
mis en jeu entre le monoxyde de carbone et l’atome de nickel ?
Le carbone porte un doublet libre : une liaison de coordination peut être établie avec le nickel.
Donner
le nom du complexe Ni(CO)4.
Tétracarbonyle nickel.
Le complexe Ni(CO)4 possède une température
d’ébullition de 316 K sous une pression de 1 bar.
Dans
les conditions de l’approximation d’Ellingham, on peut établir les
expressions suivantes pour l’enthalpie libre standard de la réaction
(1), la température T étant exprimée en Kelvin :
Pour T ≤ 316 K : DrG°(T)
= -188 + 0,502.T (en kJ.mol-1)
Pour T ≥ 316 K : DrG°(T)
= -158 + 0,407.T
(en kJ.mol-1)
Rappeler
en quoi consiste l’approximation d’Ellingham.
L'entropie DrS° et
l'enthalpie DrH° étant
supposées indépendantes de la température, les courbes d'équation DrG°(T) = DrH° - T DrS° sont des segments de droites. Les
ruptures de pente correspondent à des changements d'états physiques.
Déterminer,
à partir des expressions de l’enthalpie libre standard de la réaction
(1), l’enthalpie standard DvapH° de la
réaction de vaporisation de Ni(CO)4 sous une
pression de 1 bar à 316 K.
DvapH° =
-158 -(-188) =30 kJ/mol.
La synthèse est réalisée sous une pression totale de 1 bar à une
température supérieure à 316 K.
Indiquer
en justifiant votre réponse, comment choisir la température (basse ou
élevée) pour favoriser l’obtention du complexe.
Pour T ≥ 316 K : DrG°(T)
= -158 + 0,407.T.
DrH° = -158
kJ/mol, valeur négative : la réaction est exothermique. Une température
peu élevée favorise la formation du complexe.
Comment
peut-on séparer le complexe du monoxyde de carbone introduit en excès
?
Abaisser la température en dessous de 43°C : Ni(CO)4 passe à l'état liquide. CO reste gazeux.
|
.
Synthèse
du nickel de Raney.
Le
nickel de Raney est un catalyseur qui est obtenu par réaction d’un
alliage aluminium-nickel avec une solution concentrée d’hydroxyde de
sodium. Pour étudier les réactions mises en jeu
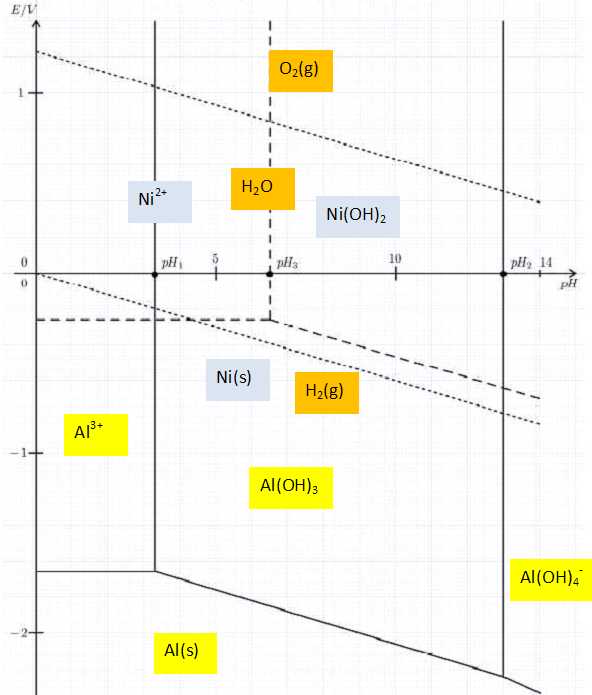
lors de son obtention, on dispose sur un même graphe :
-
du diagramme potentiel-pH de l’élément aluminium, tracé en traits
pleins pour une concentration totale en élément aluminium dissous égale
à 1 mol.L-1 et mettant en jeu les espèces Al3+(aq),
Al(OH)3(s), [Al(OH)4]-(aq)
et Al(s).
-
du diagramme potentiel-pH de l’élément nickel, tracé en traits
pointillés longs pour une concentration totale en élément nickel
dissous égale à 1 mol.L-1 et mettant en jeu les
espèces Ni2+(aq), Ni(OH)2(s)
et Ni(s).
- du diagramme potentiel-pH de l’eau tracé en traits pointillés courts
et mettant en jeu les espèces H2(g), O2(g)
et H2O(l), les pressions des gaz étant prises
égales à 1 bar.
Ces diagrammes sont tous tracés à 298 K.
Placer les domaines d’existence ou de prédominance des espèces Al3+(aq),
Al(OH)3(s), [Al(OH)4]-(aq)
et Al(s) sur le graphe.
Écrire
l’équation de la dissolution en milieu fortement basique de l’hydroxyde
d’aluminium. Donner l’expression de sa constante d’équilibre K° et
calculer sa valeur à 298 K.
Al3+aq +
4 HO-aq = Al(OH)4-aq.
(1) ß4 = 1 x 1033.
Al(OH)3(s)
= Al3+aq + 3 HO-aq
(2) ; Ks = 1 x 10-32.
(1) + (2) donne : Al(OH)3(s) + HO-aq
= Al(OH)4-aq. K = [Al(OH)4-aq] / [HO-aq]
= ß4 Ks
=1 x 1033 1 x 10-32
= 10.
Retrouver
par le calcul la valeur de la frontière pH = 13.
[HO-] = [Al(OH)4]-
/( ß4 Ks )= 1 / ( 1033*10-32,0)=
0,1 mol/L ; [H+] = Ke /
[HO-] =10-14 / 0,1 = 10-13
mol/L ; pH = -log(10-13) = 13.
Déterminer,
sans utiliser le graphique, la pente de la frontière entre les domaines
des espèces Ni(OH)2(s) et
Ni(s).
Ni2++2e- = Ni (s) = E =
-0,26 + 0,03log [Ni2+].
Ni(OH)2 =Ni2++2HO-
; Ks(Ni(OH)2) = [Ni2+]
[HO-]2
E = -0,26 + 0,03 log (Ks(Ni(OH)2
) / [HO-]2) = -0,26 +
0,02 log (Ks(Ni(OH)2
) /Ke2) + 0,03 log [H+]2.
E = -0,26 + 0,02 log (Ks(Ni(OH)2
) /Ke2) - 0,06 pH.
Un alliage d’aluminium et de
nickel est mis en contact avec une solution désaérée d’hydroxyde de
sodium concentrée (pH = 14).
Compléter
le graphe en faisant figurer les domaines des espèces H2(g), O2(g) et H2O(l).
( voir ci-dessus ).
En
déduire quelle sera l’action d’une solution d’hydroxyde de sodium à pH
= 14 sur l’alliage aluminium-nickel. Écrire l’équation de la réaction
correspondante.
Vers pH 14, couples oxydant/réducteur : [Al(OH)4]- /Al(s) ; Ni(OH)2(s)/Ni(s) ; H2O/HO-.
Les domaines relatifs à Ni(s)
et H2O ont une partie commune.
Les domaines
relatifs à [Al(OH)4]- et H2O ont une partie commune.
Al(s) et H2O appartiennent à des domaines
disjoints
L'aluminium,
réducteur le plus fort est oxydé ; l'eau est réduite. le nickel n'est pas attaqué.
Al(s) + 3H2O +HO-aq = Al(OH)4-aq + 1,5H2(g).
|
Le nickel de
Raney est utilisé comme catalyseur lors de la réduction du
paranitrotoluène noté (B) par l’hydrazine notée (Hy) en solution hydroalcoolique.
2 O2N-C6H4-CH3 + 3 H2N-NH2 = 2 H2N-C6H4-CH3 + 3 N2 + 4 H2O
En notant p l’ordre de la réaction par rapport au paranitrotoluène
(B) et q l’ordre par rapport à l’hydrazine (Hy), exprimer la vitesse volumique de la
réaction v à la date t en fonction de la constante de vitesse k et des concentrations molaires [B]t et
[Hy]t à la date t.
v = k [B]p [Hy]q.
Cette réaction a été étudiée par M.Goswami et M.Rahman à 298 K en
solution hydroalcoolique et en présence de 5,0 g.L-1 de nickel de Raney, avec
les concentrations initiales [B]0 = 5,0 × 10-5 mol.L-1 et [Hy]0 = 11 mol.L-1.
Expliquer comment se simplifie, dans ces conditions,
l’expression de v (on notera k’ la constante apparente de vitesse). Préciser le nom de cette méthode
expérimentale de détermination d’un ordre partiel.
Dégénérescence de l'ordre, l'hydrazine étant en large excès par rapport à B : [Hy]~[Hy]0 = 11 mol.L-1.
k' = k [Hy]q ; v = k' [B]p.
En faisant l’hypothèse d’un ordre 1 par rapport à (B), montrer
que la relation liant k’, [B]t et [B]0 est : ln ( [B]t / [B]0 ) = - 2 k’.t.
v = dx/dt avec x : avancement volumique en mol de la réaction ; [B]t = [B]0 -2x ; d[B]t /dt = -2 dx/dt ;
par suite v = -½d[B]t /dt = k' [B]t ; d[B]t / [B]t = -2k' dt ;
par intégration, il vient : ln ( [B]t / [B]0 ) = - 2 k’.t.
A la longueur d’onde de 275 nm, seule l’espèce (B) absorbe et
son absorbance vérifie la loi de Beer-Lambert. On note At l’absorbance de (B) à la date t et A0
son absorbance initiale.
En déduire la relation entre At, A0, k’ et t.
Absorbance et concentration sont proportionnelles. At = constante [B]t ; A0 = constante [B]0 ; ln ( At / A0 ) =- 2 k’.t.
Montrer que la courbe suivante, permet de
confirmer l’ordre 1 par rapport à (B) ; déterminer la valeur de la constante apparente de
vitesse k’ dans ces conditions expérimentales.
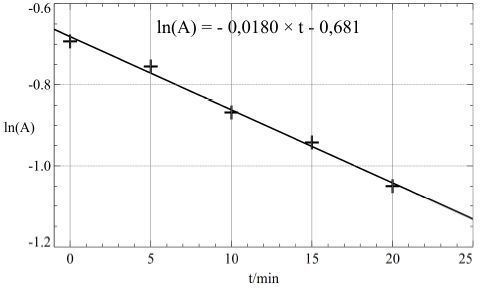
La courbe représentant ln At en fonction du temps est une droite décroissante, cela confirme l'ordre 1.
ln At =- 2 k’.t +ln A0. On identifie 0,0180 à 2k' ; k' = 9,00 10-3 s-1.
D’autres expériences ont permis de déterminer des valeurs de la
constante apparente de vitesse k’ à différentes températures, en solution hydroalcoolique
et en présence de 5,0 g.L-1 de nickel de Raney, avec les concentrations initiales : [B]0 = 5,0 × 10-5 mol.L-1 et [Hy]0 = 1 mol.L-1. On donne la courbe ln k’ en fonction de 1/T (T :
température en Kelvin).

Rappeler la relation liant la constante de vitesse k et la température T (on notera Ea l’énergie d’activation).
loi d'Arrhénius :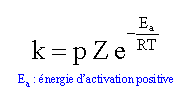
ln k = ln (pZ) -Ea / (RT)
Déduire de la courbe la valeur de l’énergie d’activation.
On identifie 1,25 104 à Ea / R ; Ea = 1,25 104 R =1,25 104 *8,31 =1,04 105 kJ mol-1.
|
|

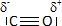 CO est
isoélectronique de N2.
CO est
isoélectronique de N2.