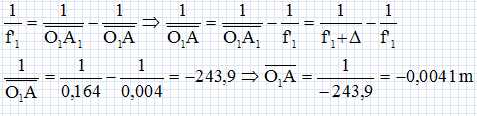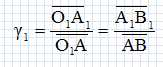Observation au microscope.
La
recherche des cristaux d'oxalate de calcium dans l'urine se fait à
l'ade d'un microscope optique au grossissement x 200 tandis que leur
dénombrement ainsi que l'évaluation des tailles moyenne et maximale
sont réalisés au grossissement x 400. Des cristaux d'oxalate de calcium
monohydraté ont des dimensions comprises entre 20 et 30 µm.
|
|
Un
microscope optique peut être modélisé par l'association de deux
lentilles convergentes de mêm axe optique,l'une étant l'objectif ( L1 : centre optique O1, distance focale f'1, grandissement g1 = -40 ) et l'autre l'oculaire ( L2 : centre optique O2, distance focale f'2=2,5 mm, grandissement commercial G2=10 ).
L'ouverture numérique de l'objectif est n sin u = 0,65 et l'intervalle optique D = F'1F2 = 16 cm.
Ce
microscope est réglé de façon que l'oeil sans défaut de
l'observateur n'accommode pas et donne d'un objet AB perpendiculaire à
l'axe optique une image finale A'B'.
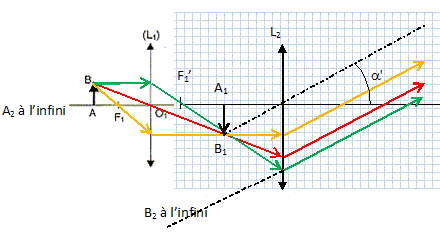
Justifier sans calcul que l'image intermédiaire A1B1 doit se former dans le plan focal objet de l'oculaire.
A1B1 joue le rôle d'objet réel pour l'oculaire. L'image A'B' de A1B1, donnée par l'oculaire se forme à l'infini : A1B1 est donc dans le plan focal objet de l'oculaire.
Compléter le schéma montrant l'image A1B1.
Définir le grandissement de l'objectif et justifier son signe.
AB et A1B1 sont de sens contraire, d'où le signe négatif. 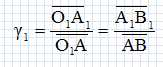
Calculer le grandissement commercial G et la puissance intrinsèque du microscope.
G 'exprime en fonction du grandissement de l'objectif et du grossissement de l'oculaire.
G = |g1 | G2= 40*10 = 400 dioptries.
Puissance intrinsèque : 4 G = 1600 d.
|
Sachant que |g1 |= D / f'1, calculer f'1.
f'1 = D / |g1 |=0,16/40 =4,0 10-3 m = 4,0 mm.
Calculer à quelle distance de O1, il faut placer l'objet AB.
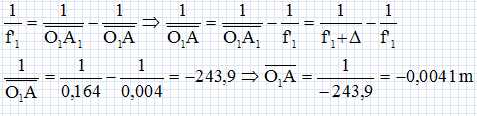
L'objet est situé à 4,1 mm devant l'objectif.
Le pouvoir séparateur ou pouvoir de résolution du microscope est donné par e = 0,61 l / (n si n u) avec l = 585 nm.
Montrer qu'il est posible d'observer les calculs rénaux à l'aide de ce microscope.
e = 0,61*585 10-9 / 0,65 =5,5 10-7 m = 0,55 µm.
"Des
cristaux d'oxalate de calcium
monohydraté ont des dimensions comprises entre 20 et 30 µm" : leurs
dimensions sont supérieures au pouvoir séparateur, on peut donc les
observer.
Dissolution de calculs rénaux.
L'oxalate de calcium CaC2O4 est un composé ionique peu soluble dans l'eau dont le pKs vaut 8,6 à 25°C.
Ecrire l'équation de l'équilibre de dissolution de l'oxalate de calcium.
CaC2O4(s) =Ca2+aq +C2O4 2-aq.
Calculer la constante de solubilité de l'oxalate d'ammonium à 25°C.
K = [Ca2+aq][C2O4 2-aq] = Ks = 10-8,6 =2,51 10-9.
Calculer la solubilité s de l'oxalate d'ammonium en négligeant les propriétés acido-basiques de l'ion oxalate.
La solution est électriquement neutre : s = [Ca2+aq]=[C2O4 2-aq] = Ks½ =(2,51 10-9 )½ =5,0 10-5 mol/L.
Expliquer
qualitativement comment la solubilité de l'oxalate d'ammonium est
modifiée dans une eau chargée en ions calcium par rapport au cas de
l'eau pure.
En présence d'ion calcium apporté par l'eau, la
concentration totale en ion calcium augmente ( par rapport à l'eau pure
). Or à température constante Ks est constant : [C2O4 2-aq], et la solubilité s vont décroître.
On
souhaite dissoudre totalement dans de l'eau des cristaux d'oxalate de
calcium. On supposera, pour les deux questions suivantes, qu'il reste
une quantité infinitésimale d'oxalate de calcium, négligeable par
rapport aux quantités d'espèces ioniques formées, mais qui confère
encore à la solution un caractère saturé.
Calculer
le volume V minimal d'eau pure nécessaire pour dissoudre complétement
des calculs rénaux d'oxalate de calcium de masse m = 20 mg. M(CaC2O4) = 128 g/mol.
Quantité de matière d'oxalate de calcium : n = m / M(CaC2O4) =0,020 / 128 =1,5625 10-4 mol.
Conservation de l'élément calcium : n(Ca2+aq) ~ 1,5625 10-4 mol ; la solution est électriquement neutre : n(Ca2+aq) =n(C2O4 2-aq).
s = n(C2O4 2-aq) / V soit V = n(C2O4 2-aq) /s = 1,5625 10-4 / 5,0 10-5 =3,1 L.
Même question en remplaçant l'eau pure par une eau minérale de concentration massique en ion calcium c0 =2,9 10-4 mol/L. On considèrera que la concentration en ion calcium ne varie pas au cours de la dissolution.
s' = Ks / c0 =2,51 10-9 / 2,9 10-4 =8,66 10-6 mol/L.
s' = n(C2O4 2-aq) / V' soit V' = n(C2O4 2-aq) /s' = 1,5625 10-4 / 8,66 10-6 =18 L.
Pour prévenir la formation de calculs rénaux, il est préconisé de boire beaucoup d'eau, la moins minéralisée possible.
Les ions calcium forment avec l'EDTA un complexe [CaY]2- dont la constante de formation est Kf =5,0 1010 à 25°C.
Ecrire l'équation de la réaction de complexation de l'ion Ca2+ par l'EDTA et exprimer la constante de formation Kf.
Ca2+ aq +Y4- aq = [CaY]2- aq. Kf = [[CaY]2- aq] / ([Ca2+ aq][Y4- aq]).
Calculer la constante de l'équilibre prépondérant dont l'équation bilan est donnée par :
CaC2O4(s) +Y4- aq = [CaY]2- aq +C2O4 2-aq.
K = [ [CaY]2- aq][C2O4 2-aq] / [Y4- aq] = [C2O4 2-aq] [Ca2+ aq] [ [CaY]2- aq] / ([Y4- aq] [Ca2+ aq])
K = Ks Kf = 2,51 10-9 *5,0 1010 =1,26 102 ~1,3 102.
K est grande : en présence d'EDTA, les cristaux d'oxalate de calcium se dissolvent.
|
|