Les bulles de savon, ondes de capillarité : bac S Amérique du Sud 2011. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Une bulle de savon est un globe formé d'un mince film d'eau savonneuse rempli d'air qui flotte dans l'atmosphère.Sa paroi est constituée de deux rangées de molécules de tensio-actif ( un tensio-actif influence la tension superficielle de ll'eau ). 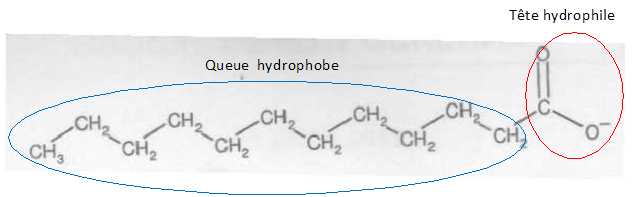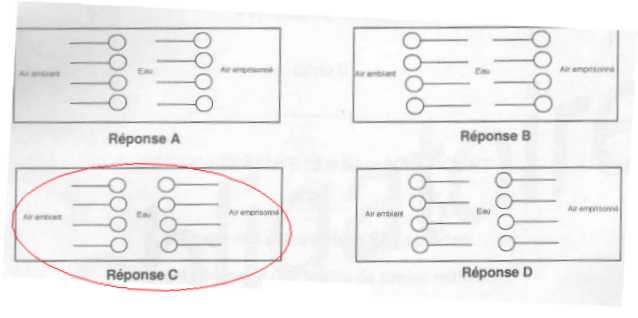Une étroite couche d'eau est retenue entre les têtes hydrophiles tandis que les queues hydrophobes, préfèrant le contact de l'air plutôt que celui de l'eau, se placent de la manière suivante : - queues de rangées externes : tournées vers l'extérieur de la bulle, donc vers l'air ambiant. - qeues de rangées internes : tournées vers l'intérieur de la bulle, donc vers l'air emprisonné. Les champions parviennent à produire des bulles de savon d'un mètre et plus. Daprès plusieurs articles de Wikipédia.. Définir les termes "hydrophile" et "hydrophobes". Hydrophile : ami de l'eau, qui a une afinité pour l'eau ; hydrophobe : qui n'aime pas l'eau. Entourer sur l'ion carboxylate ( dodécanoate) la partie hydrophile et la partie hydrophobe. L'ion carboxylate est souvent représenté schématiquement par un trait au bout duquel se trouve un cercle. Le trait représente la chaîne carbonée et le cercle le groupe carboxylate. Retrouver parmi les schémas suivants celui qui convient le mieux à la description de la paroi de la bulle de savon. La réaction d'hydrolyse basique d'un ester. L'ion dodécanoate  peut être obtenu à partir de l'hydrolyse basique du dodécanoate d'éthyle. 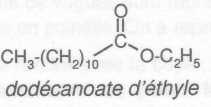Ecrire l'équation de cette réaction. Quelles sont les deux caractéristiques de cette réaction. La saponification ou hydrolyse basique, d'un ester est lente et totale. En partant de m =12,0 g de dodécanoate d'éthyle et  d'un excès d'ions hydroxyde, trouver la quantité de matière d'ion dodécanoate obtenu si le rendement de la transformation chimique est de 95 %. M(dodécanoate d'éthyle) =14*12 +28+2*16 =228 g/mol ; M(ion dodécanoate) =12*12 +23+2*16 =199 g/mol ; Quantité de matière de dodécanoate d'éthyle n = m / M(dodécanoate d'éthyle) =12,0 / 228 =5,263 10-2 mol. Quantité de matière d'ion dodécanoate  n  ; masse d'ion dodécanoate :  n M(ion dodécanoate) =5,263 10-2 *199 =10,474 g. Tenir compte du rendement : 10,144*0,95 =9,95 g. Influence de la tension superficielle sur la propagation des ondes mécaniques à la surface de l'eau. La célérité des ondes mécaniques transversales à la surface d'un liquide dépend de sa tension superficielle si la longueur d'onde est inférieure à 1,7 cm. On a alors affaire à des ondes de capillarité. La célérité d'une onde de capillarité, si la profondeur du liquide est suffisamment importante et la longueur d'onde suffisamment faible ( conditions que l'on suppose réunies dans cet exercice ), peut s'écrire : Pour observer ces ondes on peut faire vibrer un diapason en maintenant l'une de ses branches en contact avec la surface du liquide. Une onde circulaire de même fréquence que la vibration du diapason se propage alors à la surface de l'eau. Elle est difficilement observable parce que rapidement amortie, mais il est possible, en filmant le phénomène, et en faisant défiler le film image par image, de trouver une photo exploitable permettant de mesurer la longueur d'onde. On dispose de plusieurs diapason donnant plusieurs notes. note do ré mi fa sol la si do fréquence (Hz) 261 294 330 349 292 440 466 494 Expérience réalisée avec l'eau : s = 0,073 N m-1 ; r = 1,0 103 kg m-3. On choisit le diapason donnant la note la. La longueur donde mesurée est l1 = 1,33 mm. Donner la relation permettant de calculer la célérité de l'onde. Vérifier que v1 = 0,585 m/s. v1 = l1 f = 1,33 10-3 *440 = 0,585 m/s. On a représenté la surface de l'eau à la date t1. Les sommets de vagues sont représentés par des cercles en trait plein, et les creux de vagues par des cercles en pointillé. On a représenté une ligne de coupe AB. Sur ledocument 6, on a représenté la surface de l'eau en coupe, à la date t1, en faisant apparaître les points M1 et M2 ( on néglige le phénomène d'amortissement ). Choisir parmi les trois schémas du document 7 celui qui correspond à la surface de l'eau en coupe à la date t2 = t1 +½T. 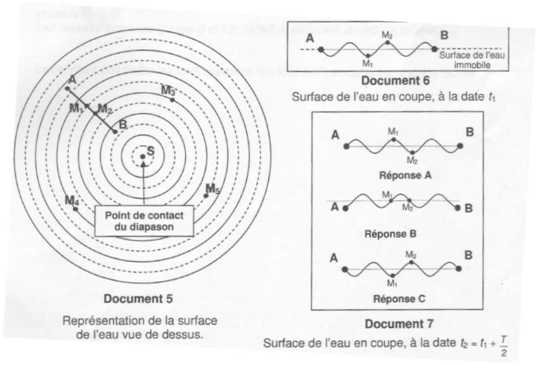A  représente en coupe la surface de l'eau à la date t1+½T. (bonne réponse ) B  représente en coupe la surface de l'eau à la date t1+0,25T ; C  représente en coupe la surface de l'eau à la date t1+T. .. .. Comparer les mouvements des points M3 et M4. Comparer les mouvements des points M3 et M5. M3 et M4 distants d'une longueur d'onde, vibrent en phase. M3 et M5 distants d'une demi-longueur d'onde, vibrent en opposition de phase. On réalise la même expérience avec un nouveau diapason de fréquence différente du premier, mais inconnue. La nouvelle longueur d'onde mesurée est l2 = 1,62 mm. La célérité est v2 = 0,534 m/s. Comment peut-on qualifier le milieu de propagation que constitue la surface de l'eau pour cette gamme de fréquence. Justifier. v1 est différent de v2 : la célérité des ondes dépend de la fréquence. La surface de l'eau est un milieu dispersif pour ce type d'onde. On garde le même diapason de fréquence inconnue, et on ajoute quelques gouttes de détergent qui se répartit à la surface et modifie la ension superficielle qui vaut alors s =0,038 N m-1. La masse volumique reste inchangée. La nouvelle longueur d'onde mesurée est l3 = 1,30 mm. Calculer la célérité de l'onde. v = (2ps / (rl)½ =(2*3,14 *0,038 / (1,0 103*1,3 10-3))½ =0,429 ~0,43 m /s. Calculer la fréquence du diapason et donner le nom de la note qu'il produit. f = v / l3 =0,429 / 1,3 10-3=3,3 102 Hz. (Mi ).

menu