.
|
|
Mesure
du niveau d’eau dans les réservoirs.
La mesure du niveau d’eau dans le réservoir est effectuée par un
ensemble émetteur et récepteur d’ondes ultrasonores situé au sommet du
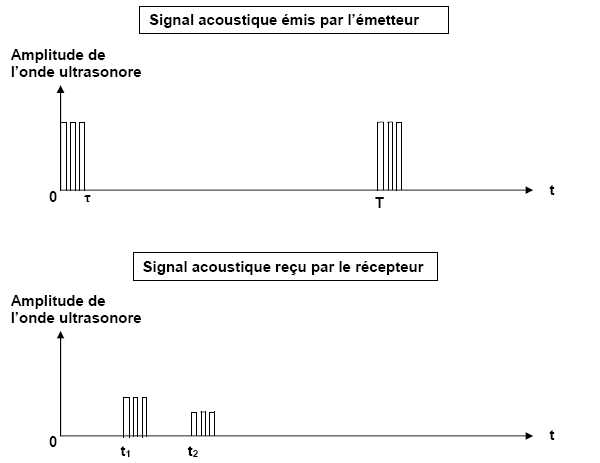
réservoir. L’émetteur produit des salves d’ondes sinusoïdales dont la
fréquence f0 est égale
à 40 kHz. Chaque salve a une durée τ, les salves sont émises toutes les
T secondes.
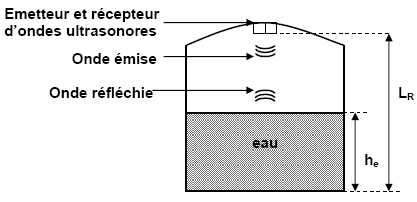
Le réservoir a pour hauteur LR = 3,00 m, il
contient de l’eau sur une hauteur he. L’onde
ultrasonore est partiellement réfléchie lors du passage de l’air dans
l’eau. Le récepteur reçoit les ondes réfléchies et les convertit en
signaux électriques qui sont ensuite traités pour afficher le niveau
d’eau dans le réservoir. L’émetteur est suffisamment directionnel pour
éviter des échos des ondes sur les parois latérales du réservoir, mais
le récepteur reçoit néanmoins deux signaux réfléchis, le second ayant
une amplitude beaucoup plus faible que le premier.
Une salve émise à l’instant t = 0 s produit deux échos reçus
respectivement aux instants t1 et t2
par le récepteur. Seul le premier, dû à la réflexion sur la surface de
l’eau contenue dans le réservoir, est pris en compte pour déterminer la
hauteur d’eau.
|
.
.
On
note ca la célérité du son dans l’air.
Exprimer la durée t1 en fonction des grandeurs LR,
he et ca.
Les ondes font l'aller et le retour entre l'émetteur et le récepteur :
la distance parcourue est 2(LR-he)en
t1 seconde à la célérité ca.
t1 = 2(LR-he)
/ ca.
En
déduire l’expression de la hauteur d’eau he en fonction de t1, LR et ca.
LR-he =½
t1ca
; he =
LR-½
t1ca.
Pour une célérité des ondes
ultrasonores dans l’air ca = 336 m.s-1
et une durée t1 égale à 5,95×10-3
s, calculer
la valeur he de la
hauteur d’eau.
he =
LR-½
t1ca
= 3,00 -0,5 *5,95×10-3
*336 = 2,00 m.
Le récepteur reçoit deux échos
pour chaque salve émise, la première correspondant à la réflexion de
l’onde à la surface de l’eau.
Proposer
une explication pour l’origine du second écho reçu.
Réflexion de l'onde sur le fond du récipient.
En fait la célérité des ultrasons dans l’air dépend de la température θ
selon le modèle mathématique suivant : ca =
0,595×θ + 331 avec θ exprimé en degré Celsius. L’isolation du refuge
garantit une température de l’eau comprise entre 4,00 ° C en hiver et
15,00 ° C en été.
Calculer
les hauteurs d’eau mesurées dans les cas extrêmes de température, pour
une durée t1 égale à
5,95×10-3 s.
ca mini = 0,595*4+331 = 333,38 m/s ; ca
maxi = 0,595*15+331 = 339,925 m/s ;
he
mini =
3,00 -0,5 *5,95×10-3
*333,38 = 2,0082 ~2,00 m.
he
maxi =
3,00 -0,5 *5,95×10-3
*339,925 = 1,9887 ~1,99 m.
La
variation de hauteur est-elle significative ? Justifier en calculant
l’écart relatif de cette variation.
(2,0082-1,9887) / 2,00 = 9,7 10-3 (0,97 %). La
variation de hauteur n'est pas sgnificative.
|
-
|
|