.
|
|
Configurations électroniques.
Donner la configuration électronique de l’atome de manganèse dans son état fondamental. Z = 25.
1s2 2s2 2p6 3s2 3p6 4s2 3d5.
Préciser à quel bloc d’éléments (s,p,d ou f) de la classification périodique appartient le manganèse. Justifier.
"3d5 " : première série des éléments de transition ( bloc d ).
Donner la configuration électronique de l’ion manganèse Mn2+.
1s2 2s2 2p6 3s2 3p6 3d5.
Radioactivité.
À
l’état naturel, un seul isotope de manganèse est stable alors que des
isotopes instables ont été mis en évidence, en particulier 52Mn, 53Mn et 54Mn.
Donner la définition des isotopes.
Des isotopes ne diffèrent que par leur nombre de neutrons. Ils ont le même numéro atomique Z.
Donner la composition du noyau 52Mn.
25 protons et 52-25 = 27 neutrons.
Le noyau 52Mn est un radionucléide émetteur ß+. Préciser la nature de la radioactivité ß+.
Emission d'un positon symbolisé par 01e.
Écrire l’équation de désintégration du noyau 52Mn en précisant les règles utilisées.
5225Mn ---> AZX +01e .
Conservation du nombre de nucléons : 52 = A +0 ; A = 52.
5225Mn ---> 5224Cr+01e .
Conservation de la charge : 25 = Z +1 d'où Z = 24 ( élément chrome ).
La loi de décroissance radioactive est donnée par la relation : N = N0 exp(-l t).
Définir les grandeurs qui interviennent dans cette relation, ainsi que leurs unités,
N : nombre de noyaux à la date t ; N0 nombre de noyaux initiaux ; t : temps en seconde ;
l : constante radioactive ( s-1).
Définir le temps de demi-vie T (ou période radioactive) d’un radionucléide.
T est la durée au bout de laquelle le nombre de noyaux initiaux est divisé par 2.
Etablir la relation entre l et T.
N(T) = ½N0 = N0 exp(-l T) ; 0,5 = exp(-l T) ; ln 0,5 = -ln2 = -l T ; l T = ln2.
Calculer l pour le noyau 52Mn. T = 5,591 jours.
l = ln2 / T = ln2 /(5,591*24*3600) =1,435 10-6 s-1.
Conductivité d‘une solution contenant des ions manganèse Mn2+.
On considère une solution aqueuse de dichlorure de manganèse(II) (Mn2+ + 2 Cl-) de concentration molaire C = 5,0 10-2 mol.L-1 = 50 mol m-3.
Donner
l'expression de la conductivité s de cette solution en fonction des
concentrations molaires des espèces en solution et des conductivités
molaires ioniques à dilution infinie. Préciser les unités des
différentes grandeurs.
s = lMn2+[Mn2+] + lCl-[Cl-].
s : S m-1 ; concentration en mol m-3 ; conductivité molaire ionique en S m2 mol-1.
En déduire alors l'expression de la conductivité s de cette solution en fonction de la concentration molaire C et des conductivités molaires ioniques à dilution infinie.
La solution est électriquement neutre : 2[Mn2+] = [Cl-] = 2C ; s =(lMn2++ 2 lCl-) C.
Calculer la conductivité molaire ionique à dilution infinie de l’ion chlorure Cl-, sachant que la conductivité molaire de la solution est s = 1,30 S.m-1. lMn2+ =10,7 10-3 SI.
(lMn2++ 2 lCl-) = s /C ; 2 lCl- = s /C-lMn2+ ; lCl- = ½( s /C-lMn2+ ) =0,5(1,30 / 50-10,7 10-3) =7,6 10-3 S m2 mol-1.
|
.
Précipitation des ions manganèse(II) et des ions manganèse(III).
Écrire l'équation de la réaction de précipitation de l'hydroxyde de manganèse(II).
Mn2+aq + 2HO-aq = Mn(OH)2 (s).
Exprimer le produit de solubilité de l’hydroxyde de manganèse (II).
Ks1 =[Mn2+aq][HO-aq]2 = 2,0 10-13.
Déterminer la concentration en ions hydroxyde de début de précipitation de l’hydroxyde de manganèse(II) pour une solution d’ions Mn2+ à la concentration molaire C' = 0,010 mol/L.
[HO-aq] = (Ks1 /[Mn2+aq])½ =( 2,0 10-13/0,010)½ =4,47 10-6 ~4,5 10-6 mo/L.
En déduire la valeur du pH de début de précipitation.
[H3O+aq]= 10-14 / 4,47 10-6 ~2,24 10-9 mol/L ; pH = -log(2,24 10-9) =8,6 ~8,7.
Écrire l'équation de la réaction de précipitation de l'hydroxyde de manganèse(III).
Mn3+aq + 3HO-aq = Mn(OH)3 (s).
Calculer le pH de début de précipitation de l’hydroxyde de manganèse(III) pour une solution d’ions Mn3+ à la concentration molaire C' =0,010 mol/L.
Ks2 =[Mn3+aq][HO-aq]3 = 2,0 10-36. [HO-aq] = (Ks2 /[Mn3+aq])1/3 =( 2,0 10-36/0,010)1/3 =5,85 10-12 mo/L.
[H3O+aq]= 10-14 / 5,85 10-12 ~1,71 10-3 mol/L ; pH = -log(1,71 10-3) =2,77 ~2,8.
On dispose d’une solution contenant les ions Mn2+ et Mn3+ à la même concentration C' =0,010 mol/L
Indiquer dans quel domaine de pH on doit se placer pour précipiter uniquement les ions Mn3+.
Le pH doit être compris entre 2,8 et 8,6.
Dosage des ions permanganate MnO4-.
Pour
déterminer la concentration molaire d'une solution (S) contenant les
ions permanganate, il a été nécessaire de faire deux dilutions.
La
solution (S) a d’abord été diluée 50 fois. La solution obtenue est
appelée solution (S’). Puis un volume de 10,0 mL de cette solution (S’)
est versé dans une fiole jaugée de 50,0 mL.
Après ajout d’eau distillée jusqu’au trait de jauge et homogénéisation, on obtient la solution (S’’).
En
utilisant un spectrophotomètre, une solution mère de permanganate de
potassium et le matériel utile à la manipulation, les mesures
expérimentales effectuées ont permis de tracer le
graphe suivant.
Préciser quelles grandeurs sont représentées en abscisse et en ordonnée.
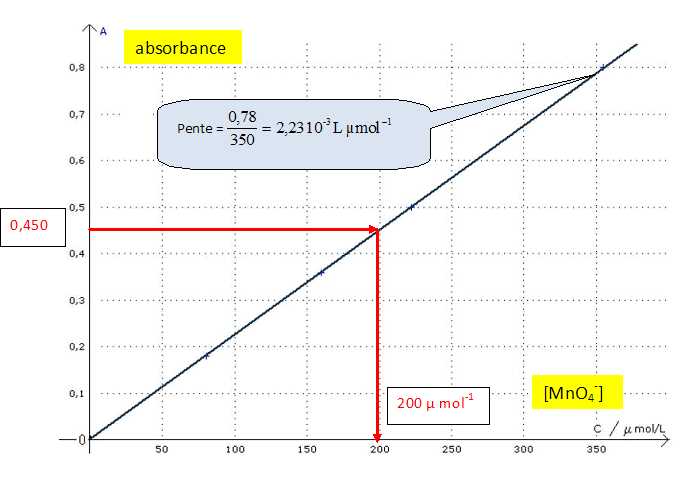
Expliquer brièvement la méthode expérimentale qui a permis d'obtenir le graphe.
Réaliser une gamme de solutions de concentration connue en ion permanganate et mesurer leur absorbance.
La loi de Beer-Lambert est-elle vérifiée ? Justifier.
Le
graphe est une droite passant par l'origine : l'absorbance est
proportionnelle à la concentration. La loi de beer-Lambert est donc
vérifiée.
La valeur de l'absorbance A de la solution (S'') est A = 0,450.
En déduire graphiquement la valeur de la concentration molaire C’’S de la solution (S’’). 200 µ mol-1.
En déduire les concentrations molaires C’S de la solution (S’), et CS de la solution S.
C'S = 5 C"S =5*200 = 1000 µmol-1 =1,00 10-3 mol/L.
CS = 50 C'S =50*1,00 10-3 =5,0 10-2 mol/L.
Dosage des ions permanganate de la solution (S) par l’acide oxalique H2C2O4.
Écrire l’équation de la réaction de dosage des ions permanganate MnO4- par l’acide oxalique (les demi-équations électroniques sont demandées).
2 fois
{
MnO4- + 8H+ +
5e- = Mn2+ + 4 H2O
}
L'oxydant MnO4-
se réduit.
5 fois
{
H2C2O4 = 2
CO2 + 2H+ +
2e-}
Le réducteur
H2C2O4
s'oxyde.
5H2C2O4
+ 2MnO4- + 6H+ = 10
CO2 + 2Mn2++
8H2O.
Préciser comment on peut détecter l’équivalence de ce dosage.
L'ion permanganate est la seule espèce colorée : il joue un double rôle : réactif et indicateur de fin de réaction.
On prélève un volume V0 = 10,0 mL d’une solution d’acide oxalique de concentration molaire CA = 0,150 mol.L-1, l'équivalence est obtenue pour un volume Ve = 12,20 mL de la solution (S) contenant les ions permanganate.
Calculer la concentration molaire CS de la solution (S).
|
avancement (mmol)
|
2MnO4-
|
+5H2C2O4
|
|
départ
|
0
|
CsVe =12,2 Cs
|
V0CA =10,0*0,150 =1,50
|
|
en cours
|
x
|
12,2 Cs-2x
|
1,5-5x
|
|
équivalence ( transformation totale)
|
xmax
|
12,2 Cs-2xmax =0
|
1,5-5xmax =0
|
xmax =1,5 / 5 = 0,3 mmol ; Cs = 2xmax /12,2 =0,6 / 12,2 = 4,92 10-2 mol/L.
Comparer le résultat obtenu à celui de la question précédente.
Ecart relatif : (5,0-4,92) /5,0 *100 =1,6 %. Les deux résultats sont cohérents.
|
-
|
|
