.
|
|
On
considère le circuit suivant :
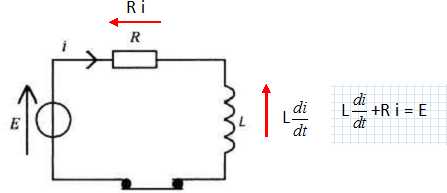 . .
Etablir
l'équation différentielle donnant l'intensité i.
Additivité des tensions : di/dt + R/L i = E/L.
La solution de cette équation est de la forme i = A exp(-R/L t )+B.
Si t tend vers
l'infini,l'intensité, notée I, est constante
; exprimer cette intensité en fonctin de E et R.
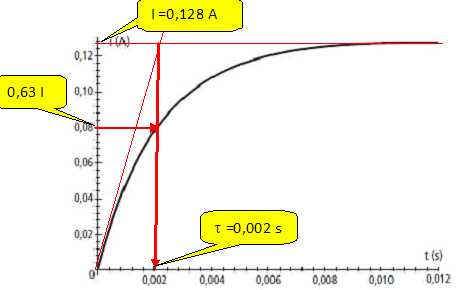
dI/dt = 0; RI = E soit I = E/R = 0,128 A ( lecture graphe ).
Exprimer
i(t) sachant qu'à t=0 l'interupteur est ouvert.
En régime
permanent I = B = E/R.
i(t=0)=0 = A +B d'où A = -B = -E/R
i(t) = E/R (1-exp(-R/L t)).
Exprimer
et déterminer graphiquement la constante de temps du circuit.
t = L / R = 0,002 s.
Calculer
L et E si R = 47 ohms.
L=R t =47*0,002
=0,094
H ; E = RI = 47*0,128 =6,0 V.
|
On
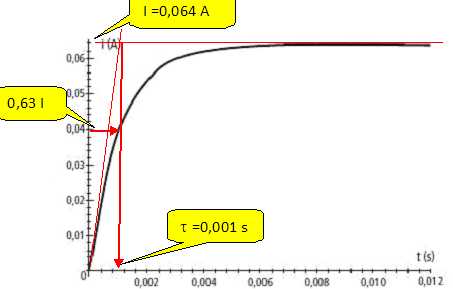
remplace la résistance R par une autre de valeur R=94 ohms.
Comment
les valeurs du courant en régime permanent et la constante de temps
sont-elles modifiées ?
On alimente le dipôle" bobine-résistance R" par un générateur basse fréquence en série avec une résistance Rg
de l'ordre de 1 kiloohm. Aucune des bornes de sortie du générateur
n'est reliée à la masse. La mesure de la résistance de la bobine donne
r = 8 ohms et R est une résistance variable.
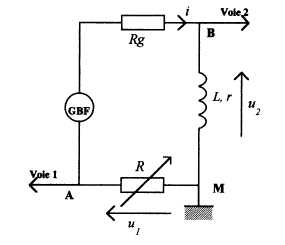
L'oscilloscope est branché comme indiqué sur le schéma. La touche "ADD" de l'oscilloscope permet d'observer la somme uS = u1 + u2.
Quel appareil permet de mesurer simplement la résistance r de la boine.
Un ohmmètre : la bobine ne faisant partie d'aucun circuit.
Exprimer en fonction de i(t), r, R et L les tensions uAM, uBM, us(t).
uAM =u1= - R i(t) ; uBM = u2 = Ldi(t) /dt + r i(t) ; uS = u1 + u2 = Ldi(t) /dt +( r-R ) i(t).
L'oscillogramme ci-dessous a été obtenu en ajustant R à la valeur de r.
Montrer que us(t) = -L/R d u1/dt.
us(t) = Ldi(t) /dt avec i(t) = -u1 / R d'où : us(t) = -L/R d u1/dt.
Déterminer graphiquement L.
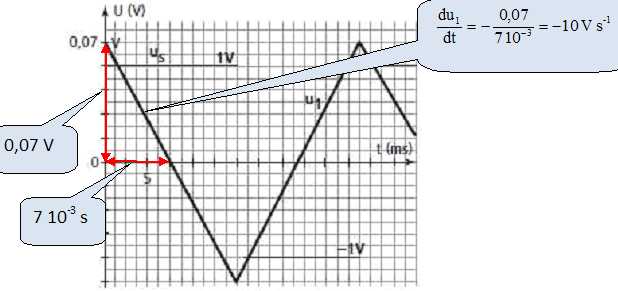
L = -us(t) R / (d u1/dt) = -1 *8 /(-10) = 0,8 H.
On
réalise le montage ci-dessous. C = 0,55 µF. On charge le condensateur
puis on bascule l'interrupteur en position 2 pour obtenir une décharge
oscillante.
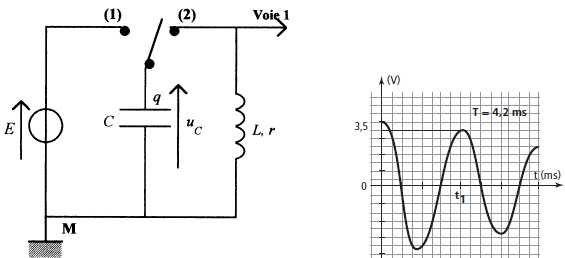
Vérifier que la pseudo-période T est homogène à un temps.
T = 2 p(LC)½. 2 p est sans dimension.
énergie = ½LI2 ; L = 2 énergie / I2 ; L s'exprime en J A-2.
énergie =½ Q2 /C ; C = Q2 /(2 énergie) ; C s'exprime en A2s2 J-1.
LC s'exprime en s2 ; (LC)½ s'exprime en seconde.
Calculer L si T = 4,2 10-3 s.
L = T2/(4 p2C) =(4,2 10-3)2 / (4*3,142 *0,55 10-6) =0,81 H.
Exprimer l'énergie emmagasinnée dans le condensateur à la date t = 4,2 ms. Calculer sa valeur en utilisant le graphique.
½Cuc2 avec uc = 3,5 V lecture graphe à la date t1 ).
½Cuc2 =0,5 *0,55 10-6 *3,52 =3,37 10-6 ~3,4 10-6 J.
Expliquer l'origine de l'amortissement des oscillations.
Au
cours des échanges d'énergies entre condensateur et bobine, une partie
de celle-ci est dissipée par effet joule dans les parties résistives du
circuit.
|
|
|



 .
.
