Charge d'un condensateur à travers une résistance. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

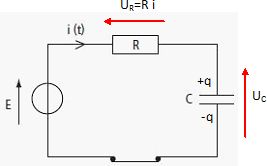
. On charge un condensateur de capacité C à l'aide d'un générateur de fem E et de résistance négligeable  par l'intermédiaire d'une résistance R. Noter sur le schéma la qharge +q du condensateur et les flèches des tensions aux bornes de la résistance et du condensateur. Etablir l'équation différentielle relative à la charge q. Additivité des tensions E = UR + UC. UR = R i ; UC = q/C et  i = dq/dt. D'où E = Rdq/dt + q/C ou dq/dt +1/(RC) q = E/R. La solution de cette équation différentielle s'écrit : q(t) = A + B exp(-t / (RC)). Lorsque t tend vers l'infini, la charge est constante. Exprimer cette charge en fonction de E et C. La tension aux bornes du condensateur chargé est égale à E et la charge est égale à E C. qinfini = E C. Exprimer la charge q(t) solution de l'équation différentielle sachant  que le condensateur est initialement déchargé. Déterminons A et B. A t=0, le condensateur est déchargé et q(t=0) = 0 ; soit 0 = A + B. q(t=0) = 0 = A + B d'où A = -B. Au bout d'un temps suffisamment grand, le condensateur est chargé et qinfini =A = E C. par suite q(t) = E C(1-exp(-t / (RC)). En déduire l'expression de l'intensité du courant dans le circuit. i(t) = dq/dt =E C / (RC) exp(-t / (RC)). i(t) = E / R exp(-t / (RC)). .  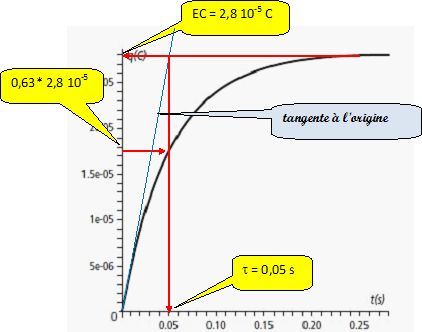L'évolution de la charge q(t) est représentée. On donne R = 11 kW, E = 6,0 V et C = 4,7 µF. Exprimer et calculer la constante de temps du circuit. t = RC = 11 10-3 *4,7 10-6 =0,0517 ~0,052 s.   Retrouver graphiquement cette valeur. 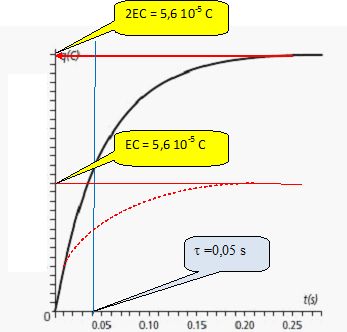On double la valeur de la tension aux bornes du générateur.   Représenter l'allure de q(t). La constante de temps du circuit sera-t-elle modifiée ? Les valeurs de R et C restent inchangées : la constante de temps du circuit n'est pas modifiée. La valeur de la charge en régime permanent est-elle modifiée ? La charge finale double et vaut 2EC.

menu