Estce
facile de stocker de l'énergie ? Certains penseront que cette question
n'a pas d'intérêt : bien sûr qu'il est bien facile de stocker de
l'énergie ! Il suffit de disposer d'un tas de charbon dans la cave,
d'une pile électrique, d'avoir un réservoir de fioul chez soi. Tout
cela permet effectivement de disposer d'une réserve d'énergie que nous
pouvons consommer quand nous le souhaitons.
Ce qui fait l'intérêt de
l'énergie ce n'est pas seulement d'en avoir, c'est d'en avoir quand
nous en avons besoin. Les énergies renouvelables ( solaire ou éolienne
), qui dépendent d'une source d'énergie ( le soleil ou le vent ) qui
n'est pas nécessairement disponible quand nous désirons qu'elle le
soit, illustrent bien ce problème. Dès lors, il est nécessaire de
pouvoir stocker de l'énergie.
|
|
Stockage de l'énergie dans une bobine.
La bobine d'allumage assure la distribution de la haute tension pour
les moteurs à essence. l'énergie est stockée sous forme électrique puis
une étincelle est produite lors de la restitution de cette énergie.
On souhaite stocker une énergie EL
dans une bobine idéale d'inductance. On dispose d'une alimentation
continue qui délivre une tension U = 6,0 V. On utilise le circuit
ci-dessous :
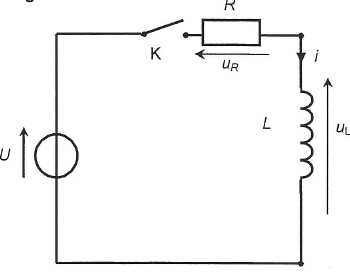
A t = 0, on ferme l'interrupteur.
A l'aide de la relation liant uL, L et i, déterminer la valeur de uL en régime permanent.
uL = L di/dt. En régime permanent, l'intensité est constante; en conséquence di/dt = 0 et uL = 0.
Montrer que l'expression de l'intensité I du courant en régime permanent est I= U / R.
Additivité des tensions : U = uR + uL= Ri +0 = RI ; I = U/R.
Exprimer l'énergie EL emmagasinée par la bobine lorsque le régime permanent est atteint.
EL =½LI2.
On souhaite que la bobine stocke l'énergie EL = 10 J en régime permanent. On dispose d'une résistance R égale à 1,8 ohms. Calculer la valeur de L pour satisfaire cette condition.
I = U / R ; L = 2 EL / I2 = 2 EL R2 / U2 = 20*1,82 / 62 = 1,8 H.
Aujourd'hui,
il existe des bobines supraconductrices capables de stocker de
l'énergie en les court-circuitant sur elles mêmes. ces bobines
possèdent une résistance interne que l'on peut considérer comme nulle.
Par exemple, une de ces bobines a une inductance de 0,10 H et peut être
parcourue par un courant I = 500 A.
Que vaut l'énergie Esupra stockée par cette bobine ?
Esupra = ½LI2 =0,5*0,10 *5002 =1,25 104 ~1,3 104 J.
|
.
Stockage de l'énergie dans un condensateur.
On charge un condensateur, préalablement déchargé, de capacité C en le
branchant en série avec une résistance R' et un générateur de tension
de force électromotrice U = 12 V. Le schéma du montage est
représenté :
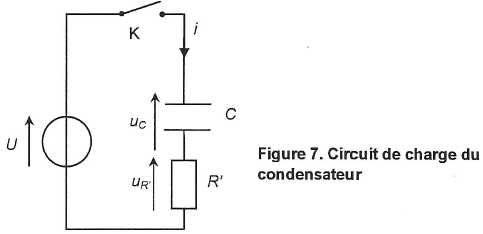
A t =0, on ferme l'interrupteur K.
Que vaut la tension uc juste après la fermeture de l'interupteur ? Justifier.
La continuité de l'énergie stockée par le condensateur, initialement déchargé, conduit à uc(t=0+) = 0.
En déduire l'expression de l'intensité i0 à cet instant.
Additivité des tensions U = uR'+uC = Ri0 + 0 ; i0 = U/R'.
L'interrupteur étant fermé depuis très longtemps, le régime permanent est atteint.
Quelle est alors la tension uC aux bornes du condensateur ?
En courant continu, un condensateur chargé se comporte comme un interrupteur ouvert : l'intensité est nulle en régime permanent.
U = uR'+uC = Ripermanent + uC ; uC = U = 12 V.
Donner l'expression de l'énergie stockée par le condensateur chargé.
EC = ½CU2.
On souhaite que le condensateur stocke une énergie EC = 10 J.
Calculer la valeur de C.
C = 2 EC / U2 =20 / 122 =0,139 ~0,14 F.
Aujourd'hui
il existe des supercondensateurs dont les capacités peuvent atteindre
le millier de farads. On utilise un supercondensateur possédant une
capacité de 800 F et dont la tension maximale à ses bornes est égale à
2,5 V.
Que vaut l'énergie Esuper stockée par ce supercondensateur lorsqu'il est chargé sous sa tension maximale.
Esuper = ½CU2 = 0,5*800 *2,52 =2,5 103 J.
Stockage hydraulique de l'énergie.
Les barrages hydrauélectriques constituent des réserves d'eau dont
l'énergie potentielle de pesanteur est utilisée pour faire tourner des
turbines génératrices d'électricité. Quand la demande d'énergie
électrique sur le réseau est faible la production excédentaire des
dispositifs non réglables ( nucléaire, solaire, éolien ... ) est
utilisée pour remonter l'eau dans les barrages d'altitude. Pendant les
pics de consommation, cette eau est relâchée à nouveau et permet la
production de l'électricité.
Donner l'expression de l'énergie potentielle de pesanteur Epp de l'eau dans un barrage d'altitude en fonction de la masse volumique r de l'eau de son volume V, de l'intensité de la pesanteur g et de la hauteur de chute h. On considère l'énergie potentielle de pesanteur nulle au niveau de la turbine et la hauteur de chute h constante.
Epp = mg h avec m = Vr ; Epp = Vr g h.
La
centrale de Grand Maison en Isère possède un réservoir de 140 millions
de mètres cubes d'eau dont la hauteur de chute est h= 0,90 km. On donne
r = 1,0 103 kg m-3 ; g = 10 m s2.
Déterminer l'énergie potentielle de pesanteur Epp pouvant être stockée sous cette forme.
Epp = Vr g h = 140 106 *1,0 103*10*900 =1,26 1015 ~1,3 1015 J.
Afin
de comparer les différents modes de stockage des trois dispositifs
étudiés, on donne, dans le tableau ci-dessous, la quantité d'énergie
pouvant être stockée par kilogramme et le temps nécessaire pour
récupérer cette énergie stockée.
| bobine supraconductrice | supercondensateur | barrage | | Energie stockée par kg | 15 kJ kg-1 | 20 kJ kg-1 | 10 kJ kg-1 | Durée minimale pour récupérer la
quasi-totalité de l'énergie stockée | 1 ms | 10 s | 10 jours | | Puissance moyenne disponible | 1,5 107 W | 2 103 W | P |
Calculer P. P = 10 103 / (10*24*3600) =1,16 10-2 ~1,2 10-2 W kg-1.
On
utilise des supercondensateurs dans les voitures électriques pour
fournir un courant d'intensité élevée au démarrage. Le
supercondensateur doit fournir une intensité constante égale à 100 A
sous une tension de 2,5 V pendant 10 s. Calculer la masse du supercondensateur nécessaire pour fournir l'énergie souhaitée au démarrage du véhicule électrique.
Energie E = U I t = 2,5 *100 *10 = 2,5 103 J = 2,5 kJ.
Masse : 2,5 / 20 = 0,125 ~0,13 kg.
|
|
|

