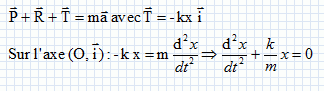.
|
|
Palet sur
une piste circulaire.
Le palet, assimilé à un point matériel, de masse
m = 70 g parcourt la piste ABC. Il quitte la piste en C avec une
vitesse inclinée d'un angle a =
45 °. Au delà de C la trajectoire est parabolique, de sommet D.Le point
B est choisi comme origine de l'énergie potentielle de pesanteur.
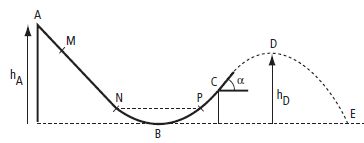
Point
|
A
|
M
|
N
|
B
|
P
|
C
|
altitude
(m)
|
1,00
|
0,75
|
0,25
|
0,00
|
0,25
|
0,40
|
vitesse
(m/s)
|
0,00
|
1,96
|
3,40
|
3,80
|
2,76
|
1,78
|
Pourquoi peut-on
affirmer, sans calculs, que l'énergie mécanique n'est pas conservée.
Les points N
et P sont à la même altitude ( h = 0,25 ). L'énergie potentielle de
pesanteur en N et en P a la même valeur. Par contre la vitesse de
passage en P est inférieure à la vitesse de passage en N. Les énergies
cinétique en P et en N sont donc différentes. L'énergie mécanique étant
la somme de l'énergie potentielle et de l'énergie cinétique, l'énergie
mécanique n'est donc pas constante.
Calculer
l'énergie mécanique en A et en C.
EM(A) = mghA+½mv2A avec vA=0.
EM(A)
= 0,070*9,8*1,00 =0,686 ~0,69 J.
EM(C)
= mghC+½mv2C = 0,070*9,8*0,40
+0,5*0,070*1,782 =0,3852 ~0,39 J.
Lors de la chute libre ( entre les points C et E ), l'énergie mécanique
se conserve.
Calculer la vitesse
en D. On donne hD = 0,48 m.
EM(C) = EM(D) =0,3852 J
EM(D) =mghD+½mv2D
; vD =(2EM(D)/
m -2ghD)½.
vD =(2*0,3852/ 0,070 -2*9,8*0,48)½ =1,2617 ~1,3 m/s.
Calculer la vitesse
en E.
EM(E)
=mghE+½mv2E
avec hE=0.
Conservation de l'énergie mécanique entre C et E : ½mv2E = 0,3852 ; vE =
(2*0,385/ 0,070)½ ~3,3 m/s.
On définit le repère orthonormé suivant : origine , le point C ; l'axe
horizontal est dirigé vers la droite ; l'axe vertical est ascendant ;
l'instant où le palet quitte la piste en C est l'origine des temps.
A
partir de la seconde loi de Newton, donner les coordonnées de la
vitesse à une date t, lors de son mouvement de chute libre.
Le palet n'étant soumis qu'à son
poids, l'accélération du palet est égale à l'accélération de la
pesanteur.
Coordonnées de l'accélération : ( 0 ; -g) ; de la vitesse initiale en C
( vc cos a ; vc
sin a ).
La vitesse est une primitive de l'accélération, d'où les coordonnées du
vecteur vitesse à la date t :
vc cos a
; -gt +vc sin a .
|
Retrouver la valeur
de la vitesse en D.
La composante verticale de la vitesse est nulle au sommet de la
trajectoire : vD = vc
cos a
= 1,78 *cos 45 =1,258 ~1,3 m/s.
Raideur d'un ressort.
Méthode 1 :
On attache à un ressort suspendu verticalement, une masse m = 200 g. L'allongement est égal à 4,9 cm.
En déduire la valeur de la raideur k.
La masse est soumise à son poids P=mg et à la tension du ressort F =
kx. A l'équilibre ces deux forces ont la même valeur : mg = kx ; k = mg
/ x = 0,200*9,8 /0,049 =40 N /m.
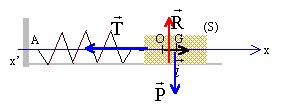
Méthode 2 :
le ressort est horizontal, l'extrémité A est fixe, l'extrémité B est
reliée à un mobile autoporteur de masse m = 400 g qui peut se déplacer
sans frottement sur un plan horizontal. Un dispositif de guidage
contraint le mobile à se déplacer sur une droite. La position du centre
d'inertie G du mobile est repérée par son abscisse x, nulle quand le
système est à l'équilibre.
Etablir l'équation différentielle vérifiée par x.
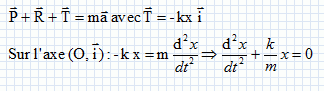
Vérifier que x(t)= Xm cos(2p/T t +F) est solution de cette équation différentielle.
x'(t) = -Xm 2p/T sin(2p/T t +F).
x"(t) =-Xm (2p/T )2 cos(2p/T t +F) = -(2p/T )2 x(t) ; repport dans
l'équation différentielle :
-(2p/T )2 x(t) +k/m= 0 soit : (2p/T )2 = k/m ou T =2p(m/k )½.
Calculer k si T = 0,63 s.
k = m (2p/T )2 = 0,400(6,28 / 0,63 )2= 39,74 ~40 N m-1.
Méthode 3 :
On
conserve le dispositif précédent. le mobile est écarté vers la
droite de telle sorte que son allongement soit égal à 7,0 cm et
lâché sans vitesse initiale.
Au passage à la position d'équilibre la vitesse est égale à v = 0,69 m/s.
En utilisant la conservation de l'énergie mécanique, en déduire une nouvelle valeur de k.
Initialement, l'énergie mécanique est sous forme potentielle élastique : ½kx2.
Au passage à la position d'équilibre ( ressort non déformé x=0 ), l'énergie mécanique est sous forme d'énergie cinétique : ½mv2.
Conservation de l'énergie mécanique : ½kx2= ½mv2.
k = mv2/ x2 =0,400 (0,69 / 0,070)2 =38,86 ~39 N /m.
|
|