.
|
|
Lampe
à vapeur de potassium.
Cette lampe émet un rayonnement constitué de quelques radiations
monochromatiques. A l'aide d'un filtre, une radiation violette est
sélectionnée. Une fente circulaire de diamètre a = 12 µm est éclairée
par cette radiation. On observe sur un écran parallèle au plan de la
fente, situé à D =15 cm de la fente, une tache circulaire de diamètre
L=1,0 cm.
Shématiser
l'expérience et représenter l'aspect de la figure de diffraction.
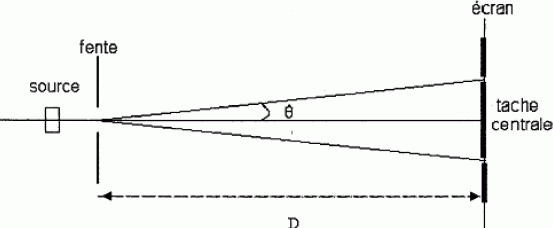 
Calculer
la longueur d'onde de cette radiation.
tan
q
~
q =
½L / D ; or q = l / a d'où : ½L
/ D = l / a soit l = a
L / (2D).
l
=12 10-6 *10-2 / (2*0,15)
=4,0 10-7 m = 0,40 µm.
Le potassium naturel contient une faible proportion de potassium 40 (4019K,
demi-vie T = 1,3 109 ans ) radioactif qui
conduit à l'argon 40. Certaines
roches volcaniques contiennent du potassium ( symbole K) dont une
partie est l'isotope 40( Z=19 ; A=40) qui se désintègre en calcium 40Ca
et en un gaz inerte l'argon 40Ar (Z=18).
En
notant l
la constante de radioartivite du potassium 40, exprimer,
en fonction du temps les nombres NK d'atomes
de potassium 40 et NA d'argon
40 présents à une date t dans un échantillon
contenant initialement N0 atomes de
potassium 40 uniquement.
au départ à t=0, N0 noyaux de potassium et aucun noyau
d'argon.
nombre de noyaux
de potassium 40 à la date t : NK=N0e-lt soit N0/
NK= elt
nombre de noyaux d'argon à la date t : NA=N0-NK
NA=N0(
1-e-lt ).
Quel âge
peut-on attribuer à une roche volcanique dont un échantillon contient
67 fois plus de potassium 40 que d'argon 40 ? Les masses
atomiques de ces deux nucléides sont pratiquement identiques.
NK / NA
=67 =N0e-lt / (N0(
1-e-lt )) = e-lt /( 1-e-lt )
67( 1-e-lt ) =e-lt ; 67 = 68 e-lt ; e-lt =
67/68 =0,9853.
ln(0,9853) = -lt ;
1,48 10-2 = lt ; l =ln2 / T = ln2 / 1,3 109
=5,33 10-10 an-1.
t =1,48 10-2
/ 5,33 10-10~ 2,8
107
ans.
|
.
Energie
de l'atome.
Quelle
preuve expérimentale établit que l'énergie des atomes ne peut prendre
que quelques valeurs bien définies. Comment s'appelle la partie de la
physique qui regroupe les lois permettant d'interpréter le comportement
des systèmes atomiques.
Les spectres d'émission ou d'absorption des atomes sont des spectres de
raies : l'énergie des photons absorbés ou émis ne peuvent prendre qu'un
petit nombre de valeurs. L'énergie de ces photons est égale à la
différence d'énergie entre deux niveaux énergétiques de l'atome. La
mécanique quantique regroupe les lois permettant d'interpréter le
comportement des systèmes atomiques.
On appelle hydrogénoïdes, un atome ( numéro atomique Z) ayant perdu
tous ces électrons sauf 1. Les niveaux d'énergie, exprimée en
eV) des hydrogénoïdes est donnée par : En
= -13,6 Z2/n2, n étant un
entier positif.
Quel ion
hydrogénoïde peut donner un atome de lithium 73Li
?
L'atome de lithium possède trois
électrons ; il doit en perdre deux : Li2+.
Calculer
la longueur d'onde de la radiation émise par cet ion lors d'une
transition du niveau n=5 au niveau n=4. A quel domaine des ondes
électromagnétiques appartient-elles ?
Z =3 ; E5
= -13,6*9/25 =-4,896 eV ; E4
= -13,6*9/16 =-7,65 eV ;
DE =E5
- E4
=-4,896-(-7,65)
=2,754 eV ou 2,754 *1,6 10-19 =4,4064 10-19
J.
DE =h c / l ; l = h c /DE =6,64 10-34
*3 108 / 4,4064 10-19
~4,5 10-7 m.
Cette valeur appartient au domaine visible [0,4 µm ; 0,8 µm ]
Cette
radiation éclaire une fente verticale de largeur a = 15 µm. Sur un
écran, situé à la distance D= 30 cmde la fente, on observe
une figure de diffraction. La tache centrale a une longueur L
= 1,8 cm.
Ces
données sont-elles en accord avec le résultat prcédent ?
l = a
L / (2D) = 15 10-6 *1,8 10-2
/ (2*0,30) =4,5 10-7 m, en accord avec la valeur
précédente.
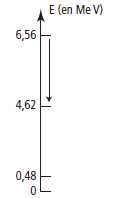 |
La
figure ci-contre donne quelques niveaux d'énergie du noyau de l'atome
de lithium. Le zéro correspond à l'état fondamental.
Comment
différencier le diagramme d'énergie de l'atome de celui de son noyau
?
Les énergies du noyau sont positives, exprimées en MeV, celle de
l'atome sont négatives, de l'ordre de quelques dizaines
d'électron-volts.
Quelle est
la longueur d'onde de la radiation émise lors de la transition fléchée
? Dans quel domaine des ondes électromagnétiques se situe-t-elle
?
6,56-4,62 =1,94 MeV = 1,94 106 eV =1,94 106
*1,6 10-19 J = 3,10 10-13
J.
l = h c /DE =6,64 10-34
*3 108 / 3,10 10-13
~6,4 10-13 m.
Cette valeur appartient au domaine des rayons gamma. |
|
|


