Pour
modifier la hauteur du son émis, le guitariste appuie sur la corde au niveau
d’une case, de façon à modifier la longueur de la corde utilisée. Des pièces
métalliques, nommées frettes, délimitent les cases sur le manche d’une guitare.
|
|
Document 1. Description du
manche d’une guitare.
La photographie
ci-dessous montre le manche d’une
guitare classique. La longueur d’une corde à vide L0 est de 65,2 cm.

Les six cordes se
différencient par leur masse par unité de longueur et leur diamètre
Document 2 : corde vibrante.
Si l’on considère
une corde vibrante maintenue entre ses deux extrémités, la hauteur du son émis
dépend de la longueur L de la corde, de sa
masse par unité de longueur μ et de la tension T de
la corde.
La composition spectrale
du son émis est complexe et la fréquence f
du fondamental est donnée par la relation :
f = 1/(2L) (T /µ)½.
Document 3 : gamme tempérée.
Les
notes se suivent dans l’ordre Do, Ré, Mi, Fa, Sol, La, Si, Do ; un
« cycle » correspond à une octave.
On envisage
10 octaves numérotées de -1 à 8.
Chaque
note d’une gamme est caractérisée par sa fréquence. Par convention, le La3
(diapason des musiciens) de l’octave numérotée 3 a une fréquence de
440 Hz.
Le
passage d’une note à la note du même nom à l’octave supérieure multiplie sa
fréquence par deux ; ainsi la fréquence du La2 est égale à 220
Hz et celle du La4 à 880 Hz.
Dans la
gamme tempérée, le quotient de la fréquence d’une note sur la fréquence de la
note précédente est égal à
21/12=1,059. Si l’on note f la
fréquence de la note Do,
note fondamentale d’une octave donnée, les fréquences des notes successives de
cette octave sont regroupées dans le
tableau suivant :| Do | Do# Réb | Ré | Ré# Mib | Mi Fab | Mi# Fa | Sol | Sol# Lab | La | La# Sib | Si Dob | Do Si# | | f | 1,059 f | 1,122 f | 1,189 f | 1,260 f | 1,335 f | 1,498 f | 1,587 f | 1,682 f | 1,782 f | 1,888 f | 2f |
Pour
une corde donnée, pour passer par exemple d’un Ré à un Ré#, le guitariste
bloque cette corde sur la case située juste à côté de
celle utilisée pour jouer le Ré, de façon à raccourcir la corde.
En s’appuyant sur les
documents donnés, répondre aux questions suivantes :
|
.
Discuter
qualitativement de l’influence de la longueur, de la tension et de la
masse par unité de longueur de la corde sur la fréquence du son émis par
une corde vibrante.
.
f = 1/(2L) (T /µ)½.
A tension et masse linéïque constantes, la fréquence est inversement proportionnelle à la longueur de la codre.
A longueur et masse linéïque constantes, la fréquence est proportionnelle à la racine carrée de la tension.
A longueur et tension constantes, la fréquence est inversement proportionnelle à la masse linéïque.
Expliquer
qualitativement comment un guitariste passe d’une note jouée Sol à la note La de la même
octave et à l’aide de la même corde.
Pour
une corde donnée, pour passer d’un Sol au La, le guitariste
bloque cette corde sur la case située deux fois plus bas que
celle utilisée pour jouer le Sol, de façon à raccourcir la corde.
Déterminer
les fréquences de Do3 et Do4.
Fréquence du La3 : 440 Hz = 1,682 fDo3 ; fDo3= 440/1,682 =261,6 ~262 Hz.
fDo4= 2 fDo3=261,6*2 =523 Hz.
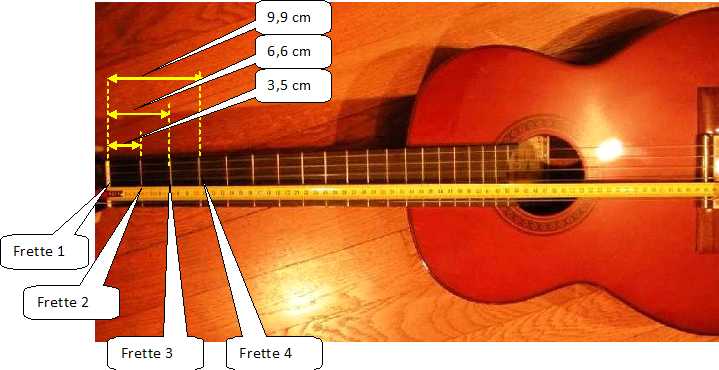
Prévoir
les positions approchées en cm des quatre premières frettes. Effectuer
ensuite quelques vérifications simples à l’aide de la photo du document 1.
f = 1/(2L) (T /µ)½.
Pour une corde donnée, (T /µ)½ est une constante : f = k/L avec k = ½(T /µ)½.
Distance du manche à la frette n° 1 : f1 / f =1,059 = L / L1 ; L1 = L /1,059 = 65,2 / 1,059 =61,6 cm. 65,2-61,6 = 3,6 cm.
Distance du manche à la frette n° 2 : L2 = L /1,122 = 65,2 / 1,122 =58,1 cm. 65,2-58,1 = 7,1 cm ( située à 3,5 cm de la frette 1).
Distance du manche à la frette n° 3 : L3 = L /1,189 = 65,2 / 1,189 =54,8 cm. 65,2-55,0 = 10,2 cm ( située à 6,6 cm de la frette 1).
Distance du manche à la frette n° 4 : L3 = L /1,260 = 65,2 / 1,260 =51,9 cm. 65,2-51,9 = 13,5 cm. ( située à 9,9 cm de la frette 1).
|
|
|

