.
|
|
On considère le système oscillant suivant :

On suppose que la
force de frottement du support sur la masse m est proportionnelle à la
vitesse ( coefficient de proportionalité µ ), mais de sens opposé à
celle-ci. Lorsque G est au dessus du point O, le ressort est au repos.
On donne m = 100 kg ; g = 9,81 m s-2.
L'expression de la période propre T0 de cet oscillateur est T0 = 2 p (m/k)½.
Que représente k ? Quelle est son unité ?
k représente la constante de raideur du ressort ; k s'exprime en N m-1.
Déduire l'expression littérale de k à partir de l'expression précédente.
T02 = 4 p2 m / k ; k = 4 p2 m /T02.
Calculer k si T0 = 0,5 s.
k = 4*3,142 *100 / 0,52 =1,58 104 ~ 2 104 N m-1.
Faire
le bilan des forces exercées sur la masse m lorsqu'elle est dans la
position indiquée sur la figure. Représenter les forces sur le schéma
sans sooci d'échelle.
La masse est soumise à son poids, verticale vers le bas,valeur mg ;
- à l'action du support, verticale vers le haut, opposée au poids ;
- à la force de frottement horizontale, de sens contraire à la vitesse, valeur µ v ;
- à la force de rappel exercée par le ressort, horizontale, dirigée vers la position d'équilibre, valeur k x.
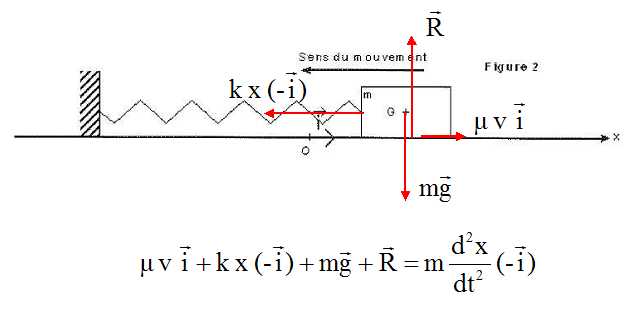
Montrer que l'équation différentielle du mouvement est du type : a +a v +k/ m x = 0 avec a = d2x/dt2 et v = dx/dt la vitesse de G.
Lorsque la masse se déplace vers la gauche, la vitesse est négative.
-µ dx/dt -kx = md2x/dt2.
d2x/dt2 + µ / m dx/dt + k / m x = 0. On pose a = µ / m.
On considère le terme a nul.
Montrer que la fonction x(t) = Xm cos ( 2p/T0 t +f) est solution de l'équation différentielle, quelles que soient Xm er f constantes.
dx/dt = Xm (-2p/T0) sin(2p/T0 +f ) ; d2x/dt2 = Xm (-2p/T0)2 cos(2p/T0 +f ).
Repport dans l'équation différentielle :
Xm (-2p/T0)2 cos(2p/T0 +f ) + k / m Xm cos(2p/T0 +f ).
((-2p/T0)2+ k / m) Xm cos(2p/T0 +f ) = 0.
Or k = 4 p2 m /T02, en conséquence (-2p/T0)2+ k / m = 0.
Par suite cette égalité est vérifiée quel que soit le temps.
Quel type d'oscillations obtient-on si le terme a est nul ?
Les oscillations sont sinusoïdales, périodiques, d'amplitude constante.
Une 2CV aborde une bosse sur la route avec une vitesse de 20 km/h.
Décrire
le mouvement de la 2 CV après le passage de la bosse si on suppose que
la suspension de chaque roue se comporte comme un oscillateur
mécnique élastique sans frottement.
La 2 CV est animé d'un mouvement sinusoïdal périodique vertical d'amplitude constante.
|
.
.
Phénomène de résonance.
La 2 CV roule à vitesse constante de 5,0 m/s sur une route
régulièrement bosselée dont la distance entre deux bosses est d = 1,00
m. La route joue le rôle d'excitateur pour la suspension de la 2 CV.
A quel type d'oscillations la suspension de la 2 CV est-elle soumise ? A quelle condition entre-t-elle en résonance ?
La
suspension est soumise à des oscillations forcées. La suspension entre
en résonance si la fréquence propre de la suspension est égale à la
fréquence de l'excitateur.
Calculer la durée Dt lorsque la 2 CV a parcouru la distance d.
Dt = d / v = 1,00 / 5,0 = 0,20 s.
Comparer Dt et T0. La suspension de la 2 CV entre-t-elle en résnance ?
Dt = 0,20 s ; T0 = 0,5 s. Dt diffère de T0, la suspension n'entre pas en résonance.
Quel élément représenté sur la figure ci-dessous, permet de limiter le phénomène de résonance ? Justifier.
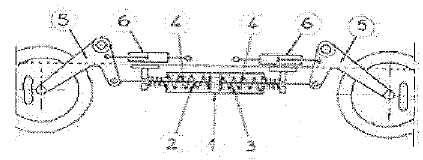
1 : pot de suspension, cylindres en tôle contenant les ressorts de suspension.
2 / 3 : ressorts de suspension à spires non jointives.
4 : les tirants, tiges d'acier assurant la liaison ressort bras de suspension.
5 : bras de suspension montés sur une traverse par des roulements.
6 : amortisseurs du type téléscopiques montés horizontalement.
Les amortisseurs : la résonance est floue ( amplitude pratiquement inexistante ) dans le cas d'un fort amortissement.
|
|
|


