.
|
|
En
1834, françois Arago invite Victor Hugo à une séance d'observation à
l'observatoire de Paris. Dans le long poème en prose " le
promontoire du songe" qu'il consacre à cette visite, Victor Hugo
raconte être monté sur la plate forme de l'Observatoire et y avoir
observé la lune. Il dit avoir utilisé une lunette qui grossissait 400
fois et rapporte qu' Arago lui soutint qu'elle ramenait la distance
entre lui et la lune de 90000 à 225 lieues. Parmi les instruments de
l'Observatoire, seuls les "objectifs de Lerebours", testés à cette
époque à l'observatoire de paris, et dont les diamètres étaient de
l'ordre de la vingtaine de centimètres, pour des distances focales de 5
à 6 m, peuvent correspondre à cette description : leur grossissement,
avec des oculaires ayant un centimètre et demi de longueur focale,
pouvaient atteindre la valeur 400 donnée par Victor Hugo.
Extrait du poème en prose.
Arago
était chez lui, il me fit monter sur la plate-forme. Il y avait là une
lunette qui grossissait 400 fois ; si vous voulez vous faire une idée
de ce que c'est qu'un grossissement de 400 fois, représentez-vous le
bougeoir que vous tenez à la main haut comme les tours de Notre-Dame.
Arago disposa la lunette et me dit : - Regardez [...]
Un instant après Arago poursuivit :
- Vous venez de faire n voyage.
- Quel voyage ?
Tout à l'heure, comme tous les habitants de la terre, vous étiez à quatre-vingt-dix-mille lieues de la lune.
- Et bien ?
- Vous en êtes maintenant à deux cent vingt- cinq lieues.
- De la lune ?
- Oui.
C'était
là en effet le résultat du grossissement de 400 fois. J'avais, grâce à
la lunette, fait sans m'en douter cette enjambée [...].
C'est cette lune-là que j'avais sous les yeux.[...]
L'effet est terrifiant.
Autre
chose que nous tout près de nous. L'inaccessible presque touché.
L'invisible vu. Il semble que l'on ait que la main à étendre. [...]
Le
champ du télescope était trop étroit pour embrasser la planète entière,
la sphère ne s'y dessinait pas, et ce que j'en voyais [...].
Au sujet du grossissement de la lunette utilisée par Victor Hugo.
On
veut vérifier que l'exemple choisi par Arago est cohérent : pour le
bougeoir dont il parle, on prendra une hauteur h = 17 cm et pour les
tours de Notre-Dame la hauteur H = 69 m. On supposera que tan a ~a.
Le
bougeoir est placé à une distance d de l'oeil de l'observateur. Cette
distance d est suffisante pour que l'approximation précédente soit
applicable.
Sur un schéma faire apparaître la distance d, le bougeoir de hauteur h et l'angle a. Exprimer en radian le diamètre apparent a du bougeoir en fonction de d et de la hauteur h.
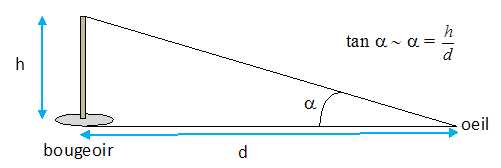
L'observateur se place maintenant à la même distance d d'une des tours de Notre-Dame.
Exprimer en radian le diamètre apparent a' de la tour en fonction de H et d.
a' ~H/d.
Vérifier que la comparaison proposée par Arago correspond bien à un grossissement G = a' / a voisin de 400.
G = a' / a = H / h = 69 / 0,17 ~4,0 102.
Pourquoi
Arago dit-il à Victor Hugo qu'il a fait un grand voyage ? Vérifier que
les distances citées par Arago sont bien dans le rapport du
grossissement G de la lunette.
Il a pu observer les détails de la lune comme s'il s'en était beaucoup rapproché.
G = 90 000 / 225 = 400.
|
.
Recherche des caractéristiques de la lunette utilisée par Victor Hugo.
Pour cette étude, on prendra la distance focale f'1 de lobjectif L1 égale à 6,0 m et pour celle de l'oculaire L2 la valeur f'2 = 1,5 cm. Les schémas ne sont pas à l'échelle de la lunette réelle.
la
lun, située à la distance D = 384 400 km de la terre, a un diamètre
moyen AB = 3 474 km et son diamètre apparent vu de la terre a une
valeur moyenne de l'ordre d'un demi degré soit a ~ 8,5 mrad.
Où se forme l'image A1B1 de la lune donnée par l'objectif L1 ?
L'image d'un objet situé à l'infini se forme dans le plan focal image de l'objectif.
Construire l'image A1B1 sur la figure.
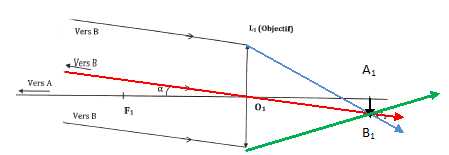
Exprimer la taille de l'image A1B1 en fonction de f'1 et a puis calculer sa valeur.
A1B1 = f'1 a = 6,0 *8,5 10-3 =0,051 m = 5,1 cm.
Image définitive A'B'.
On suppose que la lunette est afocale ce qui signifie que d'un objet à l'infini, elle donne une image définitive à l'infini.
Où doit se trouver l'image intermédiaire A1B1 par rapport à la lentille L2 ?
A1B1 sert d'objet pour l'oculaire L2. L'image définitive A'B' étant à l'infini, A1B1 se trouve au foyer objet de l'oculaire.
En déduire la position des foyers objet et image de la lentille L2 et les placer sur le schéma.
Le foyer objet de l'oculaire F2 et le foyer image F'1 de l'objectif sont confondus. Le foyer image F'2 de l'oculaire est le symétrique de F2 par rapport à l'oculaire.
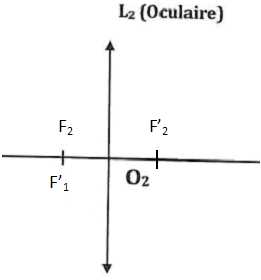
Construire l'image A'B' de A1B1 à travers la lentille oculaire L2.
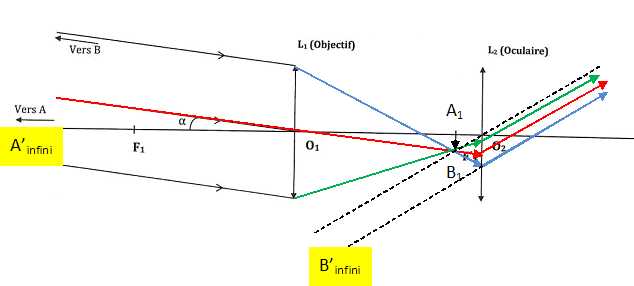
Représenter sur le schéma le diamètre apparent a' de l'image A'B' vue à travers la lunette. L'exprimer en fonction de A1B1 et de f'2.
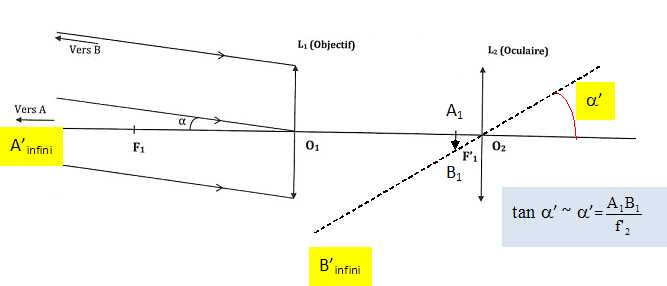
Grossissement.
Montrer que G est égal au rapport des distances focales des deux lentilles constituant la lunette. Calculer G et conclure.
G = a' / a = A1B1 / f'2 / (A1B1 / f'1) = f'1 / f'2 = 6,0 / (1,5 10-2) = 4,0 102.
Cela confirme le grossissement donné par Victor Hugo.
|
|
|



