Le
Toxotes jaculatrix, plus communément appelé poisson archer, est une
espèce d’une dizaine de centimètres de long originaire de la Polynésie
française, du Nord de l’Australie et de l’Asie du Sud-Est, bien connue
des aquariophiles. Sa technique de capture des insectes en fait un
chasseur hors-pair puisqu’il est capable à l’âge adulte d’atteindre des
proies aériennes situées à près de deux mètres.
Après une
présentation de sa technique de chasse, on modélisera le mouvement du
jet d’eau ; enfin on s’intéressera à l’éclairage des aquariums.
|
|
Etude
de texte.
«
La particularité du poisson archer est qu’il ne se contente pas
d’attendre le hasard d’une chute ou qu’un coup de vent providentiel
amène à lui cette manne céleste [les proies aériennes]. Il peut, en
projetant un puissant jet d’eau avec sa bouche, faire tomber des proies
en surface avant de les attraper […].
Après avoir repéré sa future
proie, le poisson s’oriente, se rapproche et se positionne. Le museau
affleure à la surface de l’eau mais les deux gros yeux situés près de
la bouche […] restent sous la surface […].
Précis, le tir du Toxotes
[poisson archer] est pourtant confronté à une difficulté balistique
majeure : pour viser, il lui faut tenir compte de la différence
d’indice de réfraction entre l’eau et l’air […].
Deux hypothèses ont
été proposées pour expliquer la précision du poisson archer. La
première est qu’il se positionne à la verticale de sa proie […]. Il
voit donc théoriquement l’insecte où il est vraiment. Cependant
l’observation montre que la majorité des tirs a lieu selon des angles
variant de 70° à 80°, aussi pense-t-on que plus probablement son
habileté résulte d’un apprentissage : c’est à force de rater sa cible
que le poisson corrigerait de lui-même la réfraction. On a en effet
déterminé expérimentalement qu’il est capable de tirer avec précision
environ 8 fois par minute sur une période de 10 minutes, ce qui lui
permet d’ajuster son tir si nécessaire. […]. »
Bruno Didier, Le poisson archer, Revue Insectes n°130, 2003,
Septembre, p23.
Indices de réfraction de l’air et de l’eau : nair
= 1,0 et neau = 1,33
Loi de Descartes : n1.sin i1
= n2.sin i2 avec i1
: angle d’incidence et i2 : angle de réfraction.
En prenant
appui sur le texte, nommer le phénomène physique mis en jeu lors de la
visée de l’insecte par le poisson. Dans
quelles conditions observe-t-on ce phénomène ?
La
réfraction d'un faisceau lumineux à la traversée de la surface séparant
deux milieux transparents d'indice de réfraction différents ( dioptre
eau-air dans ce cas ). Si le second milieu est moins réfringent que le
premier, le rayon réfracté peut ne pas exister.
Justifier
la phrase du texte : « Il voit donc théoriquement
l’insecte où il est vraiment ».
Le jet étant perpendiculaire à la surface de l'eau ( poisson à la
verticale sous l'insecte ), l'angle d'incidence i1
est nul. La formule de Descartes conduit à i2
=0. Un rayon lumineux perpendiculaire à la surface séparant l'eau de
l'air, n'est pas dévié.
Calculer
la fréquence f d’émission des jets d’eau.
" 8 fois par minute" : 8 / 60 = 0,13 ~1 10-1
Hz.
|
.
Modélisation du mouvement du jet d'eau.
Dans la suite de l’exercice, le comportement du jet d’eau sera assimilé à celui d’une goutte d’eau de masse m.
On note v0
le vecteur vitesse initiale du centre d’inertie de la goutte. Une
mouche posée sur une feuille située à une hauteur H = 75 cm au-dessus
de la surface de l’eau est convoitée par un poisson archer situé non
loin de là. Le poisson projette vers l’insecte un jet d’eau avec un
vecteur vitesse initiale v0 incliné d’un angle α par rapport
à l’horizontale. Le jet percute l’insecte au moment où l’eau atteint le
sommet de sa trajectoire.
Soit G le centre d’inertie de la goutte
d’eau et I le centre d’inertie de la mouche. Dans toute l’étude on
supposera que l’action de l’air est négligeable.
Le mouvement de G est étudié dans le référentiel terrestre supposé galiléen.
On
prend comme origine des dates, l’instant où le poisson archer projette
l’eau ; le point G se trouve alors au point O pris comme origine du
repère.
Données : Intensité du champ de pesanteur terrestre : g = 9,81 m.s-2 ; v0 = 4,0 m.s-1.
Étude du mouvement.
Qu’implique la phrase : « l’action de l’air est négligeable » pour le bilan des forces ?
La goutte d'eau n'est soumise qu'à son poids : la chute est qualifiée de libre.
En
déduire, en appliquant la deuxième loi de Newton dans le repère ,
l’expression vectorielle puis les coordonnées du vecteur
accélération du centre d’inertie G de la goutte.
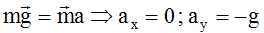
Vecteur vitesse.
Exprimer les coordonnées du vecteur vitesse initiale v0 dans le repère.
v0 x = v0 cos a ; v0 y =v0 sin a.
Soit vx la coordonnée horizontale du vecteur vitesse. Expliquer qualitativement pourquoi on peut affirmer que vx garde une valeur constante au cours du mouvement.
La
seule force agissant sur la goutte est verticale. Cette force
n'effectue aucun travail lors d'un trajet horizontal. Le théorème de
l'énergie cinétique indique que la composante horizontale de la vitesse
reste constante.
Ou bien, la vitesse est une primitive de l'accélération et la composante horizontale de l'accélération est nulle.
Dessiner, sans souci d’échelle, le vecteur vitesse (noté vS ) du centre d’inertie G de la goutte, au moment de l’impact avec l’insecte, resté immobile au point représenté sur la figure.
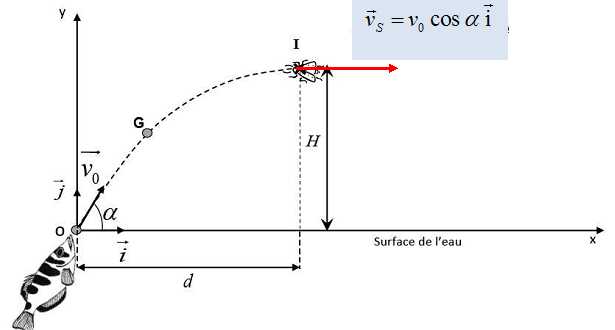
Exprimer les coordonnées de vS en fonction de v0 et α.
vS x = v0 cos a ; vS y =0.
Exprimer l’énergie mécanique du jet d’eau en fonction de m, v0, α, g et H.
Au point O, l'énergie mécanique est sous forme cinétique ( l'origine des altitudes étant prise en O).
E = ½mv02.
Au moment de l’impact avec la mouche, l'énergie mécanique est la somme de l'énergie cinétique et potentielle de pesanteur.
E = ½mv02cos2 a + mgH.
En déduire que la valeur de l’angle α permettant au jet d’eau d’atteindre la mouche vérifie l’équation : sin a = (2gH)½/v0.
La conservation de l'énergie mécanique s'écrit : ½mv02cos2 a + mgH = ½mv02.
v02(1-cos2 a ) = 2gH ; or sin2a = 1-cos2 a d'où : v02 sin2a =2gH ; sin a = (2gH)½/v0.
Vérifier que la valeur de l’angle α vaut 74°.
sin a = (2*9,81*0,75)½/4,0 =0,959 ; a = 73,53 ~74°.
Mouvement du jet d’eau.
Montrer que les équations horaires x(t) ety(t) du mouvement du centre d’inertie G de la goutte sont :
x= v0 cos a t et y = -½gt2 +v0 sin a t.
Le
vecteur position est une primitive du vecteur vitesse. La position
initiale étant l'origine du repère, les constantes d'intégration sont
nulles.
vx = v0 cos a ; x= v0 cos a t ;
vy =-gt + v0 sin a ; y = -½gt2 +v0 sin a t.
Montrer que pour que la mouche puisse échapper au jet d’eau, il faut que son temps de réaction, noté tR, soit inférieur ou égal à 0,39 s.
Durée de la montée du jet d'eau. Au sommet S, la composante verticale de la vitesse est nulle.
-gt + v0 sin a =0 soit t = v0 sin a / g = 4,0 sin 74 / 9,81 =0,39 s.
La mouche doit donc réagir avant que le jet d'eau arrive au sommet de la trajectoire.
En déduire que la distance d indiquée sur la figure a pour valeur environ 43 cm.
xS = d= v0 cos a t = 4,0 cos74 *0,39 =0,43 m = 43 cm.
|
|
|