QCM physique ( vérin hydraulique, hydrodynamique, ondes sonores ) : concours médecine. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Vérin hydraulique. Un fauteuil de dentiste peut monter et descendre à la demande du praticien grâce à un vérin hydraulique. Ce mécanisme fut inventé en 1877 par Basil Wilkinson à Baltimore. On modélise son fonctionnement par un tuyau coudé rempli dʼhuile incompressible, avec un embout cylindrique de rayon r = 1 cm à la hauteur h = 10 cm pour la commande, et un embout de rayon R = 5 cm sur lequel sʼappuie lʼassise du fauteuil à la hauteur H1 = 60 cm. La masse à soulever, patient et fauteuil, vaut M = 100 kg. Une masse m est posée côté commande pour modéliser la force dʼappui de la jambe du praticien. On note g = 10 m/s2 lʼaccélération de la pesanteur et ρ ∼ 103 kg/m3 la masse volumique de lʼhuile. Le système est en équilibre. On considère la pression p exercée dans l’huile au niveau de la surface d’appui de la masse m. 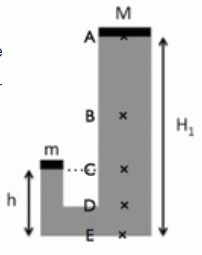1) En quel point, côté fauteuil, retrouve-t-on la même pression p ? A. p = pA ; B. p = pB ; C. p = pC ; D. p = pD ; E. p = pE. Dans un liquide homogène en équilibre, la pression est la même en tous points d'un plan horizontal : donc C. p = pC. 2) Exprimer la pression p. Cocher la ou les propositions vraies: A. p = patm ; B. p = patm + ρg(H1-h) ; C. p = patm - ρgh ; D. p = patm + mg / (πr2) ; E. p = mg / (πr2). Dans la branche de gauche, la pression exercée sous le petit piston est égale à la pression exercée par l'air augmentée de la pression exercée par le poids mg appliqué sur la surface d'aire pr2. Donc D. p = patm + mg / (πr2). On peut aussi exprimer pC= p dans la branche de droite : p = patm + ρg(H1-h)+Mg /(πR2). 3) Exprimer la pression p1 exercée dans lʼhuile au niveau de la surface dʼappui du fauteuil. Cocher la ou les propositions vraies : A. p1 = patm ;  B. p1 = patm - ρg(H1-h) ; C. p1 = p - ρg(H1-h) ; D. p1 = Mg / (πR2) ; E. p1 = patm + Mg / (πR2) La pression exercée sous le grand piston est égale à la pression exercée par l'air augmentée de la pression exercée par le poids Mg appliqué sur la surface d'aire pR2. Donc E. p1 = patm + Mg / (πR2). C'est aussi : pc-p1 = p-p1 =ρg(H1-h) d'où p1 =p-ρg(H1-h ) ; donc C. p1 = p - ρg(H1-h). 4) Calculer la masse m nécessaire pour maintenir le fauteuil à lʼéquilibre. Cocher la ou les propositions vraies : A. m < M ;  B. m > M ; C. m = 3.8 kg ; D. m = 4.0 kg ; E. m = 4.2 kg. p = patm + mg / (πr2) = patm + ρg(H1-h)+Mg /(πR2). mg / (πr2) =  ρg(H1-h)+Mg /(πR2). m = ( ρg(H1-h)+Mg /(πR2)) πr2/g. m = (104*0,5 +1000 / (3,14*0,05)2)*3,14*10-4 /10 ~4,2 kg. Donc A et E. 5) Calculer le travail W que doit fournir le dentiste pour soulever le fauteuil de H1 à H2 = 1 m. Cocher la ou les propositions vraies : A. W > 0 ; B. W < 0 ; C. |W| = 400 J ; D. |W| = 1600 J ; E. le travail est moteur pour le fauteuil. Le système étudié est le fauteuil de poids Mg. Celui-ci reçoit un travail, fournit par le dentiste : ce travail reçu par le système est compté positivement. W = Mg(H2-H1) = 1000*(1-0,6) = 400 J. Donc C et A. Le travail du poids du fauteuil est résistant ( poids : verticale vers le bas ; déplacement verticale vers le haut) 6) Calculer la hauteur Δh sur laquelle il faudrait appuyer avec la masse m pour soulever le fauteuil de H1 à H2. Cocher la ou les propositions vraies: A. Δh = 0.4 m ; B. Δh = 10 m ; C. Δh = 25 m D. Il faut un système de démultiplication pour “pomper” sur le vérin plusieurs fois pour soulever le fauteuil. E. Il ne faut pas de système de démultiplication pour “pomper” sur le vérin plusieurs fois pour soulever le fauteuil. L'huile est incompressible ; volume d'huile passant dans la branche de droite : pR2(H2-H1). Volume d'huile déplacé dans la branche de gauche : pr2Δh. pR2(H2-H1) = pr2Δh ; Δh =R2(H2-H1) / r2=(1-0,6) *52 =10 m. Donc B et D. Hydraudynamique. On modélise un tronçon de longueur 3L de lʼartère selon le schéma ci dessous et on le compare à un tronçon de même longueur de lʼartère saine. On note r le rayon de cette dernière et rʼ = 2r le rayon au niveau de lʼanévrisme. Lʼaxe Ox donne le sens dʼécoulement du sang. Le patient est allongé et lʼartère est horizontale. La vitesse du sang dans lʼartère saine vaut v = 40 cm/s et on note Q le débit sanguin. La pression sanguine à lʼentrée du tronçon, en x = 0, vaut p(0) = 13100 Pa. On prend la masse volumique du sang ρ ∼ 103 kg/m3 et on note η sa viscosité. On néglige dans un premier temps les effets de viscosité. 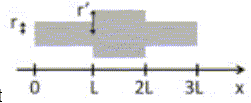1. Calculer le rapport de vitesse vʼ/v entre les parties hypertrophiée et saine de lʼartère. Cocher la ou les propositions vraies : A. Le sang ralentit dans l’anévrisme ;  B. Le sang coule à la même vitesse dans l’anévrisme et dans l’artère saine C. v’/v = 1/4 ; D. v’/v = 1 ; E. v’/v = 4. Le débit volumique est constant : Q = pr2 v = p4r2 v'  ; v' / v =0,25. Donc A et C.  2. Calculer la variation δp = pʼ-p de pression entre les parties hypertrophiée et saine. Cocher la ou les propositions vraies: A. δp > 0 ; B. δp < 0 ; C. |δp| = 85 Pa ; D. |δp| = 80 Pa ; E. |δp| = 75 Pa. Ecrire le théorème de Bernoulli pour une conduite horizontale, sans machine, sans pertes de charge. ½r(v'2-v2) +p'-p =0 ; δp  =½r(v2-v'2) = ½r(v2-(v/4)2) =½r v2(1-1/16) =0,46875 r v2 =0,46875 *1000*0,42 = 75 Pa. Donc A et E. On tient ensuite compte de la viscosité. 3. Exprimer la perte de charge Δp= p(L)-p(0) sur la première partie saine (0 ≤ x < L). Cocher la ou les propositions vraies : A. Δp a pour unité kg m s-2 ; B. Δp a pour unité kg  m-1 s-2 C. Δp est uniquement due aux frottements du sang sur la paroi de l’artère D. |Δp| = 8 η L / (π r4) ; E. |Δp| = 8 η L Q / (π r4) Δp s'exprime en pascal soit une force ( masse * accélération = masse * longueur / temps2 ) divisée par une surface  ; kg  m-1 s-2. Donc B et E. 4. On donne |Δp| = 15 Pa pour un tronçon sain de longueur L. Calculer la perte de charge |Δpʼ| due à la viscosité dans lʼanévrisme. Cocher la ou les propositions vraies : A. sur la longueur L, les frottements sont plus forts dans l’anévrisme à cause de l’hypertrophie de la paroi B. sur la longueur L, les frottements sont plus forts dans l’étroite artère saine que dans l’anévrisme C. |Δp’| = 0.9 Pa ; D. |Δp’| = 3.8 Pa ; E. |Δp’| = 60 Pa Les frottements fluides sont proportionnels à la vitesse et  v' < v ; donc B. |Δp| = 8 η L Q / (π r4) ; |Δp'| = 8 η L Q / (π 16r4) ; |Δp'| = |Δp| /16 =15/16 ~0,9 Pa. Donc C. 5) Dessiner sur le graphe ci-contre lʼallure de la pression p(x) pour une artère totalement saine pour 0 ≤ x ≤ 3L. Cocher la proposition vraie : La perte de charge est égale à 15 Pa pour une longueur L soit 45 Pa pour x = 3 L ; p(x) =13100-15 x/L ; p(3L) ~13055. Donc D. 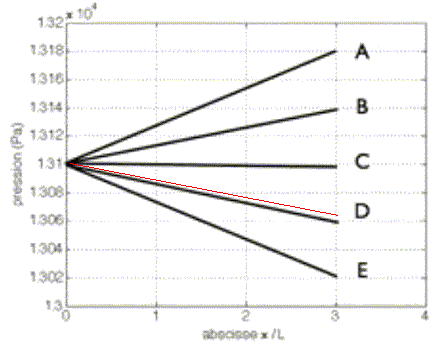6) Même question pour lʼartère malade étudiée ci dessus. Cocher la proposition vraie : E. Aucune des courbes dessinées n’est vraie. 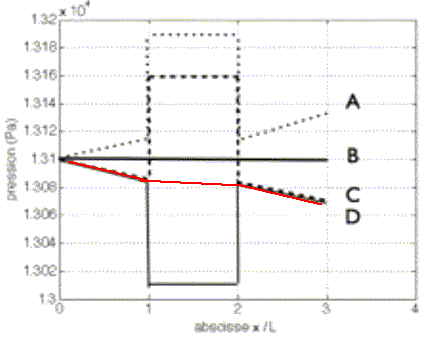Donc C. 7. Calculer la pression sanguine p(3L) en sortie du tronçon dans le cas avec anévrisme. Cocher la ou les propositions vraies : A. p(3L) = 13 130 Pa ; B. p(3L) = 13 100 Pa ; C. p(3L) = 13 070 Pa ; D. p(3L) donne la pression réelle dans le sang E. p(3L) mesure une surpression par rapport à la pression atmosphérique. p(3L) = 13100-15-0,9-15 ~ 13069 Pa. Donc C. La pression sanguine est égale à la différence entre la pression exercée par le sang sur la paroi des artères et la pression atmosphérique ; donc E. 8) Un tronçon dʼartère saine a une résistance hydraulique R sur une longueur L. On considère l’artère saine, de longueur 3L. On note Ra sa résistance et Pa la puissance perdue par viscosité. Cocher la ou les propositions vraies : A. Ra = R/3 ;  B. Ra = 3R ; C. |Pa| = Δp / Ra ; D. |Pa| = Δp2 / (3R) ; E. |Pa| = 3 Δp2 / R. Ra est proportionnelle à la longueur, donc B. Puissance  = force * vitesse = pression * surface * vitesse ( Pa m3 s-1). R s'exprime en Pa s m-3 ; D est homogène du point de vue des unités et Ra = 3 R. Ondes sonores. Un haut-parleur, d’une puissance sonore P = 6,28 mW, émet un son audible de manière isotrope dans une salle de bains où règne la pression atmosphérique patm. On note Z = 400 kg m-2 s-1 l’impédance acoustique de l’air. L’intensité de référence pour 0 dB vaut Iref = 10-12 W/m2. L’air se comprime comme un gaz parfait de pression p, de volume V, de température T, d’indice adiabatique γ = 7/5. Dans les conditions adiabatiques du passage de l’onde sonore, le produit pVγ reste constant. Vous écoutez le son du haut-parleur dans votre bain, la tête hors de l’eau, à la distance r =5½ = 2,23 m. 1. Exprimer l’intensité I sonore entendue à cette distance. Cocher la proposition vraie : A. I = P / r ; B. I = P / (π r2) ; C. I = P / (4π r2) ; D. I = r P ; E. I = π r2 P. 2. Calculer le niveau sonore L en décibels à cette distance. Cocher la proposition vraie : A. L = 80 dB ; B. L = 86 dB ; C. L = 94.5 dB ; D. L = 98 dB ; E. L = 105 dB. I = P / (4π r2)=6,28 10-3 /(4*3,14*5) =1,0 10-4 W/m2. N = 10 log (I / I0) =10 log (10-4 / 10-12) =80 dB. Donc A. 3. Calculer l’amplitude maximale de surpression pa perçue à cette distance. Cocher la ou les propositions vraies: A. pa = 0.08 Pa ; B. pa = 0.28 Pa ; C. pa = 5 Pa ; D. la pression dans l’air perçue par l’oreille varie entre patm et patm+2pa E. la pression dans l’air perçue par l’oreille varie entre patm-pa et patm+pa. Vrai. La pression acoustique p crée par un son d'intensité acoustique I se propageant à la célérité c dans un milieu de masse volumique r est donné par la relation: p2 =r I v = Z I p en pascal ; I en watt m-2 ;  v en ms-1. p2 =10-4 *400 =4,0 10-2 ; p =0,20 Pa. 4. On étudie les variations de pression, de température et de volume au passage de l’onde sonore. Cocher la ou les propositions vraies: A. dp/dV = γ p / V ; B. dp/dV = - γ p / V ; C. dT/T = [γ / (1-γ)] dp/p ; D. dT/T = [(γ-1) / γ] dp/p ; E. dT/T = γ dp/p. Différencier  pVγ = Cste : Vγ dP +PgVg-1dV=0.  pVγ = Cste s'écrit : P(1-g) Tg = cste (1-g) ln P +g ln T = Cste' ; passer à la dérivée logarithmique : (1-g) d P  / P +g dT /T =0 : donc D. 5. Calculer la variation relative maximale de température due au passage de l’onde sonore à la distance r = √5 m. Cocher la ou les propositions vraies : A. l’air refroidit très légèrement au passage de l’onde sonore B. l’air se réchauffe très légèrement au passage de l’onde sonore C. |dT/T| = 8.0 10-7 ; D. |dT/T| = 3.8 10-6 ; E. |dT/T| = 9.8 10-6. (1-g) d P  / P +g dT /T =0 ;  dT /T =(g-1) /g d P  / P = 0,4 / 1,4 *0,20 / 105 ~6 10-7, donc B. Vous plongez la tête dans l’eau, sans changer la distance au haut-parleur. L’interface air/eau à un coefficient de réflexion en intensité R = 0,999. 6. Calculer le niveau sonore Lt transmis dans l’eau. Cocher la ou les propositions vraies : A. Lt = L - 0.04 dB ; B. Lt = L - 30 dB ; C. Lt = L - 3 dB ; D. Lt = L + 3 dB ; E. Lt = 50 dB. Intensité incidente I = 10-4 W m-2 ; intensité transmise  I / 1000 = 10-7 W m-2 ; Lt = 10 log (It / I0) =10 log (10-7 / 10-12) =50 dB. Donc B et E. 7. Une bulle d’air est restée coincée contre chaque tympan. Calculer le niveau sonore L’ perçu par les tympans. Cocher la ou les propositions vraies : A. L’ = L - 0.08 dB ; B. L’ = L - 60 dB ; C. L’ = L - 15 dB ; D. L’ = 20 dB ; E. L’ = 35 dB. L’interface air/eau à un coefficient de réflexion en intensité R = 0,999. Intensité incidente I = 10-7 W m-2 ; intensité transmise  I / 1000 = 10-10 W m-2 ;  L' = 10 log (It / I0) =10 log (10-10 / 10-12) =20 dB. Donc B et D. 8) Les vibrations de l’eau sont aussi transmises au crâne. Sachant que la conduction osseuse atténue de 20 dB le niveau perçu par l’oreille interne par rapport au niveau qui atteint le crâne, calculer le niveau sonore L” ainsi perçu. Cocher la ou les propositions vraies : A. L” = L’ + 20 dB ; B. L” = L’ - 20 dB ; C. L” = Lt - 20 dB ; D. L” = Lt + 20 dB ; E. L” = 30 dB. 9) Quel niveau sonore Lfin captez-vous finalement ? Cocher la ou les propositions vraies : A. Lfin est la valeur minimale entre Lt, L’ et L” ; B. Lfin = 20 dB ; C. Lfin = 30 dB ; D. Lfin = 35 dB ; E. Lfin = 50 dB. Intensité sonore transmise  au tympan  à travers l'oreille et la bulle d'air : 10-12 10L'/10 = 10-10 W m-2. Intensité sonore transmise  au tympan  par conduction osseuse : 10-12 10L"/10 = 10-9 W m-2. Total : 1,1 10-9 W m-2. Lfin =10 log (1,1 10-9 / 10-12) =30,4 dB.

menu