|
On notera g= 10 m s-2 l'intensité du champ de pesanteur et r la masse volumique de l'eau. Un séisme dont l'épicentre noté E est situé sous la mer, peut être responsable d'un tsunami.
Le tsunami est une déformation globale de l'océan qui se propage à la vitesse v = (gh)½ avec h, profondeur de l'océan.
La période des oscillations liées au séisme est T = 2 s ; la profondeur de l'océan autour de l'épicentre E est h = 1 km.
Donner la valeur de la longueur d'onde autour de E.
l =vT = (gh)½T =(10*1000)½*2 = 200 m.
La
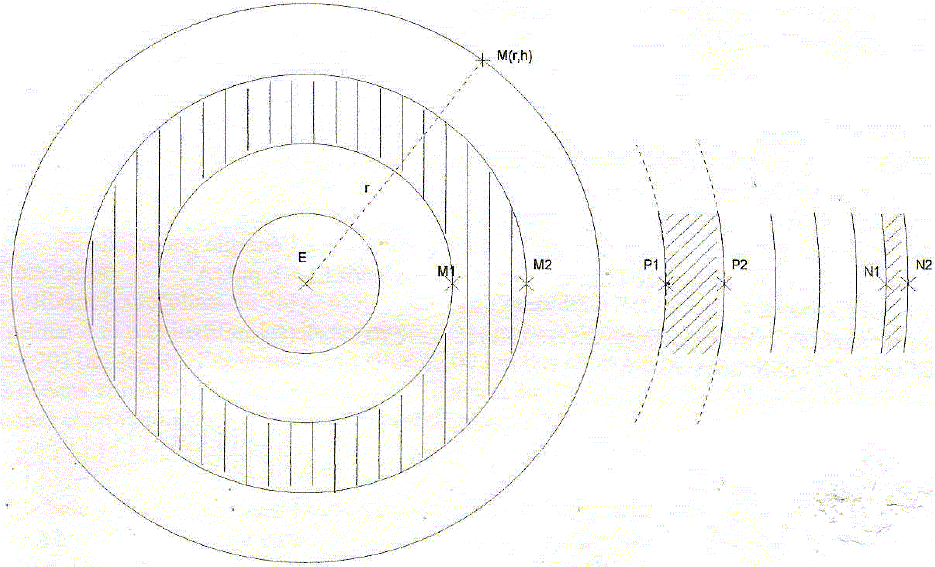
figure suivante représente la position des points " hauts" de l'océan
autour de l'épicentre E à un instant donné. l'amplitude d'oscillation
en un point M notée A(r,h) dépend de la distance r à l'épicentre et de
la profondeur h de l'océan en ce lieu.
|
Comparer la profondeur des océans en M1 et N1. Déterminer la profondeur de l'océan en N1.
La distance entre deux points "hauts" consécutifs est égale à la longueur d'onde.
l1 =M1M2 ~ 2 cm ; l2 = N1N2 =0,5 cm.
l = (gh)½T ; T et g étant constant, la longueur d'onde est proportionnelle à la racine carrée de la profondeur h.
l1 =4 l2 donc la profondeur en M1 est le double de la profondeur en N1.
Profondeur en N1 : 0,5 km.
|
Pour
déterminer l'évolution de l'amplitude avec r et h on utilisera la
modèlisation de la surface de l'océan présentée par les figures
suivantes. Le profil sinusoïdal de l'océan est remplacé par un profil
rectangulaire. 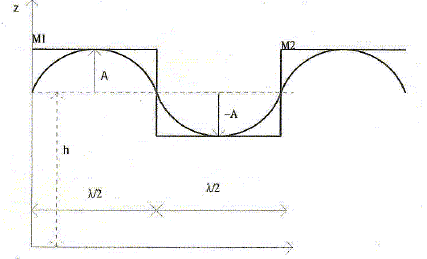
La déformmation de la surface d'eau est ainsi grossièrement modèlisée entre M1 et M2, c'est à dire pour une longueur d'onde par la figure ci-dessous. 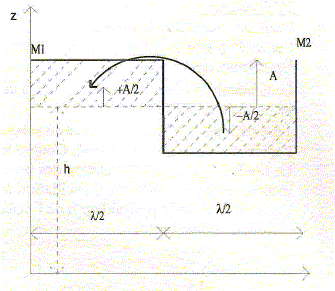
Par
rapport à la situation d'un océan au repos d'énergie potentielle de
pesanteur nulle ( trait en pointillés ), la présence d'une perturbation
entre M1 et M2 correspod à une énergie potentielle non nulle.
Pour
évaluer cette énergie potentielle de pesanteur, on peut considérer que
la situation finale correspond à la situation initiale après
translation d'une masse d'eau ( hachurée sur la figure ) d'une altitude
initiale h-½A à une altitude finale h =½l A.
Variation de A avec r.
On cherche à établir l'énergie potentielle de pesanteur liée à la déformation de l'océan entre r et r+l ( zone hachurée ). La longueur d'onde est supposée petite par rapport à r.
Montrer que l'énergie potentielle de pesanteur liée à la déformation de l'océan entre r et r+l s'écrit : Ep = k r g l rA2. Identifier la constante k.
La variation de l'énergie potentielle de pesanteur est égale à l'opposée du travail du poids de la masse d'eau m = V r.
V : volume d'eau compris entre les deux cercles de rayons r et r+ ½l. Hauteur de l'eau A.
V = p ( r+½l)2A-pr2A =pA( 2r+½l)½l ~pArl.
m = V r=prArl.
Travail du poids : W = -mgA
Variation de l'énergie potentielle : mgA = p r g l rA2. On identifie k à p.
Après propagation, la même énergie est concentrée enntre r' et r'+l.
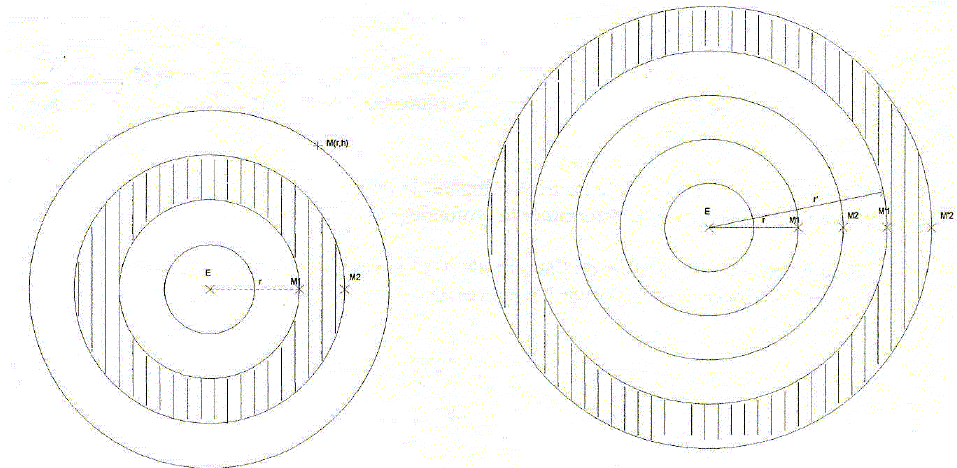
En déduire l'évolution de A avec r.
La même énergie se retrouve dans un plus grand volume d'eau.
Si r augmente, k r g l étant constant, le carré de l'amplitude diminue ( si r est multiplié par 4, alors A est divisée par 2 ).
p r g l rA2= p r g l r'A'2 ; A = A' (r' / r)½.
Variation de A avec h.
On
cherche à établir les énergies potentielles de pesanteur liées à la
déformation de l'océan pour les deux zones hachurées sur la figure
suivante, éloignées de l'épicentre ( rP proche de rN).
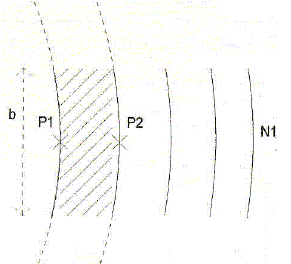
Montrer que l'énergie potentielle de pesanteur liée à la déformation de l'océan entre P1 et P2 et pour la bande de largeur b s'écrit : Ep = k' r g lP bAp2. Identifier la constante k'.
Faire un raisonnement identique au précédent en modifiant la masse m d'eau.
Demi-volume d'eau hachuré ( assimilé à un rectangle ) de hauteur Ap. V' =½ b lp Ap.
m' = ½b lp Ap r d'où Ep =½b lp Ap2 r g. On identifie k' = ½.
Après propagation, la même énergie est concentrée entre N1 et N2 pour une bande de même largeur.
En déduire l'expression de l'amplitude AN en fonction de Ap, lp et lN, puis en fonction des profondeurs des océans hp et hN.
Même type de raisonnement entre N1 et N2 : m" = ½b lN AN r d'où Ep =½b lN AN2 r g.
Conservation de l'énergie potentielle : ½b lp Ap2 r g =½b lN AN2 r g.
lp Ap2 = lN AN2 . AN =Ap ( lp / lN)½.
Or l =vT = (gh)½T d'où : AN =Ap ( hp / hN)0,25.
|
|
En utilisant les résultats précédents, montrer que A(r,h) = A =Cste ra hß.
D'une part : Ap = AN (rN / rp)½ avec h constant.
L'amplitude est proportionnelle à r-½.
D'autre part : AN =Ap ( hp / hN)0,25avec r constant.
L'amplitude est proportionnelle à h-0,25.
Justifier les dégâts causés par ce phénomène.
Pour un épicentre proche des côtes r est faible et l'énergie potentielle est grande.
De plus la profondeur de l'océan diminue à l'approche des terres : h-0,25augmente. L'amplitude augmente ( si h est divisée par 100, l'amplitude triple ( 1000,25 ~3,2).
Lors
du séisme du 11 mars 2011 au japon, l'épicentre était situé à 100 km
des côtes les plus proches, la profondeur de l'océan voisine de 1 km.
Une alerte au Tsunami était-elle possible à Sendai ( port le plus proche) et en Polynésie ? ( un petit calcul est demandé)
La célérité des ondes étant de l'ordre du km /s , une alerte est impossible à Sendai.
Par contre, en Polynésie, située à près de 10 000 km de distance, ( 10000 s ~ 3 h ) l'alerte est possible.
Une
baie communique avec l'océan par un détroit de largeur d, avec une
profondeur d'eau égale à h = 1 km. Suivant la valeur de d,la côte
de la baie est plus ou moins touchée par le tsunami.
Discuter qualitativement ( un petit schéma explicatif serait le bienvenu ).
On rappelle que la période du séisme est proche de quelques secondes.
l =vT = (gh)½T =(10*1000)½*2 = 200 m.
Si la largeur du détroit est du même ordre de grandeur que la longueur d'onde, on observe un phénomène de diffraction. 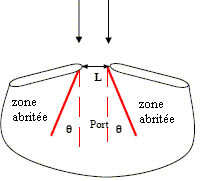
q= l/L.
|
|





