Ondes, cyclotron, radioactivité, spectre d'émission, oscillateur électrique : concours Orthoptie Marseille  2010 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

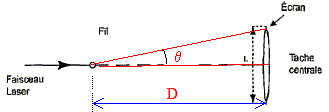
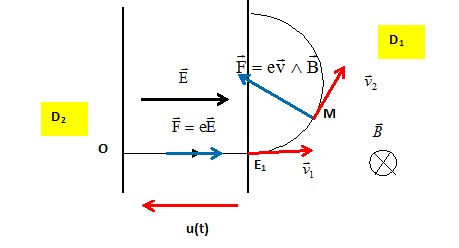
Ondes progressives. Une onde progressive plane monochromatique de longueur d'onde l = 500 nm traverse une fente de largeur a = 0,25 mm. Les taches de diffraction sont observées sur un écran placé à une distance D = 1 m de ce trou. Quel est la largeur q de l'écart angulaire entre le centre de la tache centrale et la première extinction ? q = l / a =500 10-9 / 0,25 10-3 =2 10-3 rad. Quelle sera la largeur de la tache centrale de diffraction ? ( on considère que q est très faible ). L = lD/(2a) =500 10-9 *1 / 0,5 10-3 =1 10-3 m = 1 mm. Le cyclotron. Un cyclotron est constitué de deux demi-cylindres D1 et D2 creux, séparés par une distance L petite devant leur rayon. Le tout est placé dans le vide. Un champ magnétique uniforme B, perpendiculaire à l'axe des cylindres est créé dans D1 et D2. Que se passe t-il lorsqu'on introduit un proton ( de charge q = e) dans D1 avec une vitesse v0 perpendiculaire à B et à la face plane de D1 ? Décrire et justifier la trajectoire du proton. La particule chargé, animée de la vitesse initiale v0, placée dans un champ magnétique B est soumise à la force de Lorentz. Le poids du proton est négligeable devant cette force ; la force de Lorentz perpendiculaire à la vitesse, ne travaille pas. La valeur de la vitesse reste constante : le mouvement est uniforme. La force de Lorents, donc le vecteur accélération est centripète ( dirigée vers le centre du demi-cylinde D1) : le mouvement est circulaire. 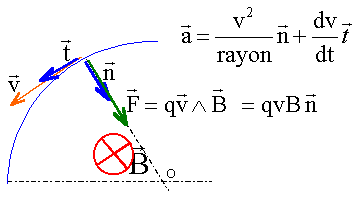Donner en fonction de la charge (q) du proton, de sa masse m, de v0 et B, l'expression du rayon R de la trajectoire. Ecrire la seconde loi de Newton dans la base de Frenet : L'accélération est centripète de norme qvB/m = v² /rayon. En conséquence : dv/dt =0, le mouvement est uniforme ( norme de la vitesse constante) et qvB = mv² / rayon ; rayon = mv / (qB). R = mv0 / (qB).     Exprimer le temps t mis par le proton pour décrire cette trajectoire en fonction de m, q et B. La demi-circonférence de rayon R est parcourue à la vitesse v0 enpendant la durée t : p R = v0t ; t = pR/v0 avec R/v0 = m / (qB) ; t = pm/(qB). A la traversée du proton entre D1 et D2, on applique une différence de potentielle U pour accélérer le proton. Quelle sera l'expression du rayon R' de la trajectoire du proton dans D2 s'il a été accéléré d'un facteur 1,5 entre D1 et D2 ? La vitesse passe de v0 à 1,5 v0 donc R' = 1,5 R R' = 1,5mv0 / (qB). Justifier le fait que cette tension U entre D1 et D2 soit alternative et donner l'expression de sa fréquence. Pour une accélération maximale, à chaque demi tour, la tension alternative doit changer de signe ( la vitesse ayant changer de sens ) et prendre sa valeur maximale. La demi période de la tension alternative est égale à la durée d'un demi tour. T = 2t = 2p m / (eB). f = 1/T = eB /(2p m). Radioactivité. L'uranium 233 23392U est radioactif a. Ecrire l'équation de désintégration et donner le nombre atomique de masse de l'espèce formée. 23392U --->AZX + 42He. Conservation du nombre de nucléons : 233 = A+4 d'où A = 229. Conservation de la charge : 92 = Z+2 d'où Z = 90. Quelle est en MeV l'énergie totale libérée par cette réaction ? On donne les masses en u : m(23392U) = 233,0395 u ; m(AZX) =229,0316 u ; m(42He) = 4,0026 u. 1 u = 931,5 MeV/c2. Variation de masse : Dm = m(42He) + m(AZX) -m(23392U) =4,0026+229,0316-233,0395 = -5,3 10-3 u. Energie libérée : -5,3 10-3 *931,5 = -4,94 ~ -4,9 MeV. Le signe négatif traduit le fait que le système cède de l'énergie au milieu extérieur. En négligeant les énergies cinétiques du noyau 23392U et du noyau formé, quelle est l'énergie cinétique de la particule alpha émise ? L'énergie libérée par la fissiuon de l'uranium est emportée par la particule a sous forme d'énergie cinétique : 4,9 MeV. Spectre d'émission. L'analyse du spectre d'émission d'une lampe à vapeur de sodium révèle la présence de raies de longueurs d'onde bien définies. Justifier la discontinuité du spectre. Les énergies de l'atome sont quantifiées, seules un petit nombre de valeurs sont possibes. A quelle différence d'énergie correspond l'émission de la raie de longueur d'onde l = 589 nm ( J et eV) ? On donne h = 6,62 10-34 Js ; c = 3 108 m/s ; e = 1,6 10-19 C. E = hc / l = 6,62 10-34 * 3 108  / 589 10-9 =3,37 10-19 ~3,4 10-19 J. 3,4 10-19  / 1,6 10-19  = 2,1 eV. Quelle est la fréquence de ce rayonnement ? E = h n ; n = E / h =3,37 10-19 /  6,62 10-34  =5,09 1014 ~5,1 1014 Hz. De quel type de rayonnement s'agit-il ? Dans l'air, une radiation dont la longueur d'onde est comprise entre 400 nm et 800 nm appartient au domaine visible. Oscillateur électrique. Un condensateur de capacité C = 1 µF dont la tension initiale est UAB = 10 V est connecté à la date t = 0 à une bobine d'inductance L = 25 mH. En négligeant la résistance de la bobine, le modèle mathématique qui décrit les oscillations non amorties dans le circuit est : uAB (t) = Umax cos ( 2pt/T0). Donner la valeur de Umax. uAB (t=0) = Umax  = UAB = 10 V. Donner la période T0 de ce circuit. T0 = 2 p (LC)½ = 6,28 (0,025*10-6)½ =9,93 10-4 ~9,9 10-4 s. Donner l'expression de l'intensité électrique dans le circuit. i(t) = dq/dt avec q = C u(t) : i(t) = Cdu(t) / dt. i(t) =CUmax(-2p/T0) sin ( 2pt/T0). Calculer la valeur de imax. imax = CUmax(2p/T0) = 10-6*10*6,28 / 9,93 10-4  =6,32 10-2 ~6,3 10-2 A. Exprimer les énergies Ec(t) et Eb(t) emmagasinées respectivement dans le condensateur et la bobine. Ec(t) = ½C u2(t) = ½C U2max cos2 ( 2pt/T0). Eb(t) = ½Li2(t) = ½L(CUmax(2p/T0))2 sin2 ( 2pt/T0). Or (2p/T0)2 =  1/(LC) d'où Eb(t) =½C U2max sin2 ( 2pt/T0). Exprimer l'énergie totale E. Conclure. Calculer sa valeur. E = Ec(t) + Eb(t) =½C U2max ( cos2 ( 2pt/T0)+ sin2 ( 2pt/T0) = ½C U2max. L'énergie totale est constante. E = 0,5 * 10-6 *102 =5 10-5 J.

menu