|
Lumière,
mouvement d'un cycliste, radioactivité :
concours Orthoptie Amiens 2010 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||
| .
. |
|||||||
|
|||||||
|
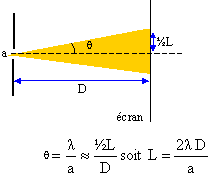
Quel est le type de lumière ( monochromatique ou polychromatique ) émise par une lampe à vapeur de sodium ? Justifier. Monochromatique signifie : une seule radiation, une seule fréquence, une seule couleur. " 94 radiations dont deux intenses " : lumière polychromatique. Dans ces conditions, l'indice de réfraction de l'air vaut n = 1,000273. Calculer les longueur d'onde dans le vide de chacune des radiations de l'énoncé. n = c / vair ; lair = vair / f ; l0 = c / f ; l0 = n lair . l0 =1,000273* 588,9950 =589,1558 nm ; l0 =1,000273* 589,5924 =589,7534 nm ; Calculer la fréquence de chacune de ces radiations dans le vide, puis dans l'air. La fréquence est une caractéristique de l'onde : elle ne dépend pas du milieu de propagation. Les fréquences sont identiques dans l'air et dans le vide. f = c / l0 =299 792 458 / 589,1558 10-9 =5,088 509 1014 Hz ; f = c / l0 =299 792 458 / 589,7534 10-9 =5,083 353 1014 Hz. Un faisceau de lumière émise par la lampe à vapeur de sodium tombe, sous une incidence i, sur la face d'un prisme de verre. Qu'observe t-on à la sortie du prisme ? Quel nom donne t-on à ce phénomène ? Comment qualifie t-on le verre du prisme ? Définir ce type de milieu. 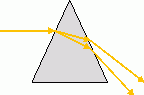 Chaque radiation est réfractée sur les faces d'entrée et de sortie du prisme. Or l'indice du verre dépend de la fréquence de la radiation. On observe un étalement ( dispersion ) du faisceau à la sortie. Le verre est un milieu dispersif pour la lumière : la célérité des radiations dans le verre dépend de leurs fréquences. Seule la radiation de longueur d'onde 588,9950 nm est dirigée vers une fente F de largeur a = 50 µm. Sur un écran placé à une distance D = 1,2 m derrière la fente une figure apparaît. Indiquer le nom associé à ce phénomène. représenter schématiquement l'expérience. Calculer la valeur d = ½L de la distance séparant le milieu de la frange centrale de la première extinction. On observe un phénomène de diffraction de la lumière par la fente dont la largeur est du même ordre de grandeur que la longueur d'onde de la lumière.
L= 2*588,9950 10-9 * 1,2 / 50 10-6 = 2,827 10-2
m voisin 2,8 cm. On considère un cycliste et sa bicyclette. La masse totale de l'ensemble vaut m = 80 kg et on prendra g = 9,8 m s-2. Les conditions initiales sont les suivantes : le cycliste s'engage dans une descente rectiligne de longueur L = 300 m assimilée à un plan incliné faisant un angle a = 3 ° avec l'horizontale, sa vitesse est v0 =14,4 km/h, sa position est repérée par son abscisse x comptée à partir du début de la descente qui s'effectue en roue libre et suivant l'axe de plus grande pente. On considère que toutes les forces sont appliquées au centre de gravité G. Les forces résistantes sont négligées. Représenter par un schéma les forces en présence sur le centre de gravité G ; établir l'expression de l'accélération a subie par G. Préciser le nom donné à ce mouvement. Le système est soumis à son poids, vertical, vers le bas, valeur mg et à l'action du plan perpendiculaire au plan. Ecrire la seconde loi de Newton sur un axe parallèle au plan et orienté vers le bas. Ce mouvement est rectiligne uniformément accéléré. 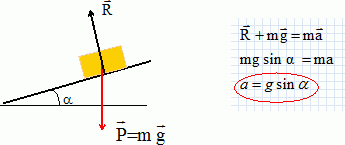 Etablir l'expression de la vitesse v de G en fonction du temps. Le vecteur vitesse est une primitive du vecteur accélération. v = at + constante ; à t = 0, la vitesse initiale vaut v0 d'où v = g sin a t + v0. Etablir l'expression de la position x de G en fonction du temps. Le vecteur position est une primitive du vecteur vitesse. x = ½at2 + v0t + constante. A t = 0, le mobile se trouve à l'origine de l'axe : la constante est nulle. x = ½g sin at2 + v0t. Calculer le temps mis par le cycliste pour arriver au bas de la descente. v0 = 14,4 / 3,6 = 4,0 m/s ; x = L = 300 m ; a = 9,8 sin 3 = 0,513 m s-2. 300 = 0,5 *0,513 t2 + 4 t ; t2 + 15,6 t -1,17 103 = 0. Discriminant : D = 15,62 + 4*1,17 103 = 4922 ; D½ =70,16 ; t = (-15,6 +70,16) / 2 = 27,3 s ~27 s. En déduire la vitesse ( km/h) du cycliste en bas de la descente. v = g sin a t + v0 = 9,8 sin 3 *27,3 + 4 =18,0 m/s ou 18,0*3,6 =64,8 ~65 km/h. Le cycliste effectue un virage sur un plan horizontal, sa trajectoire est une portion de cercle de rayon R = 57 m et sa vitesse a une valeur constante 65 km/h. Faire un schéma représentant la trajectoire et placer les vecteurs vitesse et accélération. préciser le nom donné au vecteur accélération et calculer sa valeur. L'accélération est centripète. 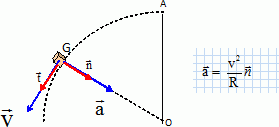 a = v2 / R = 182 / 57 =5,68 ~5,7 m s-2.
Radioactivité. On considère le phosphore 3215P. Le noyu de phosphore radioactif a une masse égale à 31,97622 u. Donner la composition de ce noyau. 15 protons et 32-15 = 17 neutrons. Calculer la masse de l'ensemble des nucléons séparés. mproton = 1,00728 u ; mneutron = 1,00866 u ; 1 u correspond à 931,5 MeV. m =15 mproton + 17 mneutron = 15*1,00728 + 17 *1,00866 =32,25642 u. Calculer le défaut de masse du noyau. Dm = 31,97622-32,25642 = -0,2802 u. Calculer en MeV l'énergie de liaison du noyau. El = |Dm|*931,5 =0,2802*931,5 = 261,0 MeV. Calculer l'énergie de liaison par nucléon. Comment varie cette grandeur avec la stabiité du noyau ? El / 32 =261,0 / 32 = 8,156 MeV / nucléon. Les noyaux les plus stables ont la plus grande énergie de liaison par nucléon. Le phosphore 3215P se désintègre en soufre 3216S. Ecrire la réaction de désintégration. Quelle est la particule émise ? 3215P = 3216S +0-1e La particule émise est un électron. Le noyau de phosphore 3215P est trop riche en neutrons. Quelle réaction se produisant dans le noyau permet de confirmer l'émission de la particule précédente ? Un neutron se transforme en proton 10n = 11p +0-1e La désintégration du phosphore 32 en soufre 32 libère de l'énergie. De quel type d'énergie s'agit-il et qui emporte cette énergie ? L'électron émis emporte cette énergie sous forme d'énergie cinétique.
|
|||||||
| |
|||||||
|
|