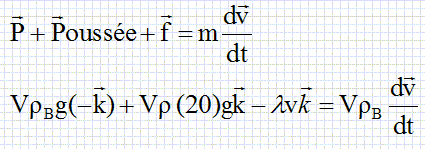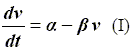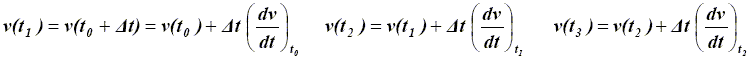Le
thermomètre de Galilée est un instrument de mesure de la température
ambiante T. Il est constitué d’un tube cylindrique en verre scellé
contenant un liquide transparent dans lequel sont plongés des boules
numérotées de masses différentes mais de volume identique V. Dans toute
l’étude, on suppose chaque boule parfaitement sphérique et de densité
homogène (en réalité, les boules ont deux extrémités en pointe, un
petit médaillon indiquant la température étant accroché à l’extrémité
inférieure).
La particularité du thermomètre provient du fait que la
masse volumique du liquide ρ(T) diminue sensiblement quand la
température T (en degrés Celsius) augmente.
Données : ρ(20°) = 1001 kg.m-3 ; ρ(21°) = 1000 kg.m-3 ;
Volume boule : V = 10-6 m3 = 1 cm3.
Accélération de la pesanteur : g = 10 m.s-2.
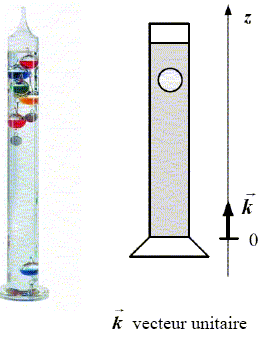
A T = 20°C, la boule A, complètement immergée, est en équilibre dans le liquide.
A T = 21°C, c’est la boule B qui est en équilibre dans le liquide.
On note respectivement ρA et ρB les masses volumiques des boules A et B.
Etude en statique :
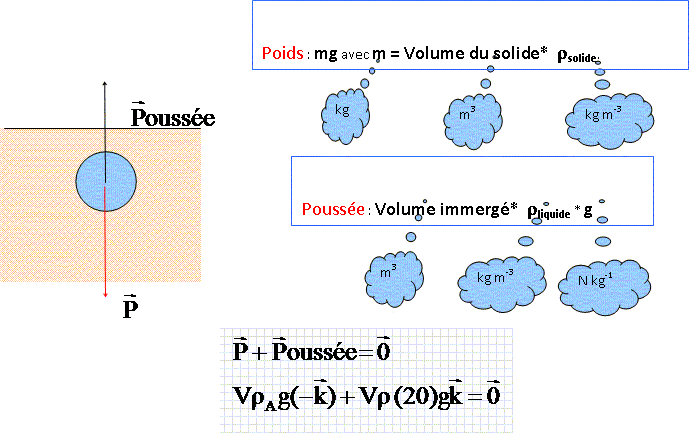
Nommer les forces qui s’exercent sur la boule A.
Chaque boule est en équilibre sous l'action de son poids et de la poussée d'Archimède.
|
Par
application de la première loi de Newton, écrire l’équation vectorielle
d’équilibre s’appliquant au centre de gravité de la boule A, immobile,
en équilibre dans le liquide, en fonction de g, ρ(20°), ρA, V et k.
|
En déduire la masse volumique ρA de la boule A.
rA = r(20).
Quelle est alors la masse volumique ρB de la boule B ? Calculer la différence de masse des boules A et B, soit Δm = mA - mB, exprimée en milligramme.
rB = r(21).
Δm = mA - mB= VrA -VrB = V(r(20)-r(21))=10-6 (1001-1000) = 10-6 kg = 1 mg.
La température ambiante est de 21°C. On suppose que le tube ne contient que les deux boules A et B. Représenter sur un schéma les positions respectives des 2 boules.
La poussée est identique sur les deux boules de même volume, plongée dans le même liquide.
Or mA > mB
; le poids de la boule A est supérieur à celui de la boule B. La boule
A est au fond, tandis que la boule B est en équilibre au sein du
liquide. | 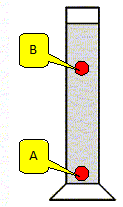 |
Etude en dynamique : La température ambiante est maintenant de 20°C. La boule B est maintenue au fond du tube jusqu’à l’instant t0 = 0 s. A l’instant t0 = 0s, elle est libérée et se met alors en mouvement pour remonter dans le liquide. Soit v sa vitesse en m.s-1
et t le temps en seconde. La force de frottement subie par la boule B
dans sa remontée est représentée par 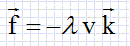 avec λ = 10-4 kg.s-1. avec λ = 10-4 kg.s-1.
Par application de la deuxième loi de Newton, écrire l’équation
vectorielle s’appliquant au centre de gravité de la boule B en fonction
de g, ρ(20°), ρB, V, λ, v, dv/dt et k.
La boule B est soumise à son poids, vertical vers le bas, valeur VrBg, à la pousée d'Archimède, verticale, vers le haut, valeur Vr(20)g et à la force de frottement . 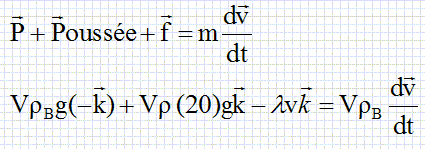
La vitesse v(t) de la boule B obéit alors à une équation différentielle de la forme : 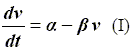
Quelles sont les unités respectives de α et β ?
dv/dt a la dimension d'une acélération : a a donc la dimension d'une accélération ( m s-2 ).
[ ßv ] = LT-2 ave [v]= L T-1 donc [ß] = T-1 ( s-1).
Exprimer α et β en fonction de g, ρ(20°), ρB, V et λ . Calculer α et ß.
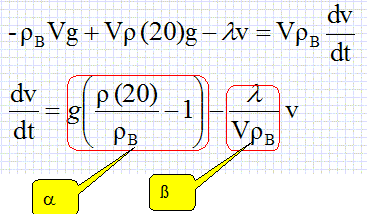
a = 10(1001 / 1000 -1) = 0,01 m s-2; ß =10-4 / (10-6*1000) =0,1 s-1.
Exprimer la vitesse limite vlim de la boule B et calculer sa valeur.
Lorsque la vitesse limite est atteinte, le mouvement est rectiligne et uniforme : dvlim/dt=0.
a-ßvlim=0 ; vlim = a / ß = 0,01 / 0,1 = 0,1 m s-1.
|
|
On
se propose maintenant d’appliquer la méthode numérique d’Euler à la
résolution de l’équation différentielle (I). Cette méthode permet de
calculer, pas à pas, les valeurs de la vitesse de la boule B à
différents instants. Δt est le pas de calcul en temps. A l'instant t0 = 0s, v(t0) = 0 m s-1 et (dv/dt) t0= a.
Les formules donnant la vitesse aux instants t1, t2, et t3 sont :
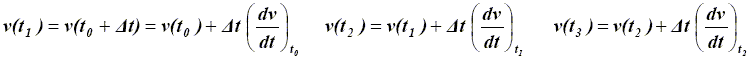
On pose Δt = 5 s. Calculer les vitesses v(t1), v(t2) et v(t3).
v(t1) =0 + 5*0,01 =0,05 m s-1.
(dv/dt) t1=a-ßv(t1) =0,01-0,1*0,05 =0,005 m s-2.
v(t2) =0,05+ 5*0,005 =0,075 m s-1.
(dv/dt) t2=a-ßv(t2) =0,01-0,1*0,075 =0,0025 m s-2.
v(t3) =0,075+ 5*0,0025 =0,0875 m s-1.
|
|



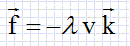 avec λ = 10-4 kg.s-1.
avec λ = 10-4 kg.s-1.