Concours audioprothésiste : la catastrophe de Tchernobyl ; voyage lunaire. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

La catastrophe de Tchernobyl : Suite  à l'explosion d'un des réacteurs de la centrale de Tchernobyl le 26 avril 1986, une grande quantité d'éléments radioactifs a été libérée dans l'atmosphère. parmi les éléments radioactifs composant ce nuage, on distingue principalement l'iode 131 et le césium 137. Partie A : l'iode 131 a une demi-vie t½ = 8 jours.    Calculer la constante radioactive l de l'iode 131. l = ln2 / t½ = ln2 / 8 = 8,664 10-2 =~8,7 10-2 jour-1 ou ln2 / (8*24*3600) = 1,0028 10-6 ~1,0 10-6 s-1. 100 kg de noyaux d'iode radioactif ( A = 131) ont été émis dans l'atmosphère. NA = 6,02 1023 mol-1. Calculer l'activité due à l'iode 131 dans le nuage radioactif au moment de l'explosion.   Quantité de matière d'iode 131 : n = m /M = 100 000 / 131 =763,4 mol. Nombre de noyaux d'iode 131 : N = n NA =763,4*6,02 1023 =4,61 1026 noyaux. Activité A = l N =1,0 10-6 *4,6 1026 =4,61 1020 Bq. A son arrivée en France, l'activité du nuage due à l'iode 131 a été mesurée à 6,00 1019 Bq. 80 % de l'iode radioactif émis est retombé près du site. Remarque : nous avons remplacé la valeur 2 1018 Bq par 6 1019 Bq afin que le temps trouvé corresponde mieux à la réalité. Calculer le temps mis par le nuage pour atteindre la France, distante de 3000 km du site de l'explosion. Quelle a été la vitesse moyenne du nuage radioactif ? Activité de l'iode 131 dans le nuage après retombées : A0=0,20 * 4,61 1020 =9,22 1019 Bq. Ecrire la loi de décroissance radioactive : A =A0 exp(-lt). ln (A0/A) = lt ; t = ln (A0/A) / l =ln(9,22 1019 / 6,00 1019) / 8,664 10-2 = 4,96~5,0 jours ou 119 heures. Vitesse : 3000 / 119 = 25,2 ~25 km/h. Partie B. La constante radioactive du césium 137 est de 2,31 10-2 an-1. Quel est le pourcentage de noyaux de césium radioactif restant dans l'atmosphère aujourd'hui (  04 /2006 ) par rapport à la quantité émise lors de l'explosion ? Ecrire la loi de décroissance radioactive : N =N0 exp(-lt). ln (N/N0) = -lt avec t ~20 ans. ln (N/N0) = -2,31 10-2 *20 = -0,462 ; N/N0 = 0,63 ( 63 %).   En quelle année auront disparu 95 % des noyaux de césium 137 libérés dans l'atmosphère ? Ecrire la loi de décroissance radioactive : N =N0 exp(-lt) avec N = 0,05 N0. ln (N/N0) = -lt  = ln 0,05 =-2,996. t = 2,996 / 2,31 10-2 ~130 ans soit en l'an :130+1986 =2116. Voyage lunaire. Autour de la lune. Une fusée abritant des astronautes se satellise autour de la lune sur une orbite circulaire à 100 km d'altitude. Faire un schéma sur lequel sera ( seront ) représentée(s) la ( les ) force(s) exercée(s) sur la fusée. La fusée est soumis à la seule force de gravitation de la lune, force centripète attractive. 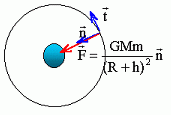Démontrer que le mouvement du centre d'inertie de la fusée est uniforme. La force de gravitation centripète est perpendiculaire, à chaque instant, à la vitesse : cette force ne travaille pas. L'énergie cinétique, et en conséquence la valeur de la vitesse, ne sont pas modifiée : le mouvement est donc uniforme. Calculer cette vitesse. Dépend-elle de la masse de la fusée ? 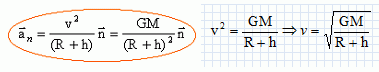La masse de la fusée ne figure pas dans l'expression de la vitesse : cette vitesse est indépendante de la masse de la fusée. A.N : M =7,35 1022 kg ; G = 6,63 10-11 SI ; R = 1,74 103 km ; h = 100 km. R+h = (1,74 103 +100 ) km = 1,84 106 m. v = (6,63 10-11*7,35 1022 / 1,84 106)½ =1,6274 103 m/s ~1,6 km/s. Déterminer la période de révolution de la fusée autour de la lune. Ecrire la 3è loi de Kepler : 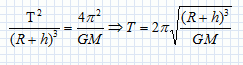T =2*3,14 ((1,84 106)3 /(6,63 10-11*7,35 1022))½ =7,1 103 s Sur la lune. Lors de leur manipulations sur la lune, les astronautes font tomber une caisse, sans vitesse initiale, en bas d'une paroi rocheuse haute de 10 m. Retrouver par le calcul la valeur du champ de gravitation sur le sol lunaire. g = GM / R2 =6,63 10-11*7,35 1022 / (1,74 106)2 =1,62 N/ kg. Donner l'expression de la position Z(t) et de la vitesse V(t) du centre d'inertie de la caisse en fonction du temps au cours de la chute. On choisit un axe vertical orienté vers le bas ; l'origine de l'axe est la position du centre d'inertie de la caisse à t = 0, haut de la falaise. Z(t )= ½gt2 et V(t) = gt. En déduire la durée de la chute et la vitesse au moment de l'impact au sol du centre d'inertie de la caisse. t = (2 H / g)½ avec H = 10 m. t = (20 / 1,62)½ =3,514 ~3,5 s. v = 1,62 *3,514 =5,7 m/s. Les rapports. Vous recevez deux rapports de l'expédition lunaires dont les extraits suivent. Rapport n°1 : pour freiner notre atterissage sur le sol lunaire, nous avons ouvert les parachutes du module.... Quelle ne fut pas notre fierté de voir notre étendard flotter et onduler sur le sol lunaire.... Suite à une maladresse, la caisse s'écrasa en bas du ravin en un bruit fracassant... Rapport n°2 : Avant que le module lunaire n'entre en contact avec le sol, nous avons actionné les rétrofusées afin de diminuer notre vitesse pour un atterrissage en douceur... Quelle ne fut pas notre surprise de découvrir les traces de pas intactes dans la poussière lunaire laissées par la précédente expédition... Je pris mon élan et sautait en bas du ravin de 10 m pour récupérer la caisse qui était malencontreusement tombée... L'un des rapports est faux. Lequel ? Justifier. Le rapport n°1 est faux : sur la lune il n'y a pas d'atmosphère. Les parachutes ne servent à rien, ils ne se gonflent pas. Le drapeau ne flotte pas " au vent" et le bruit ne peut pas se propager dans le vide.

menu