Moteur de Stirling, étude thermodynamique : concours Caplp maths sciences  2011 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Généralités sur les moteurs dithermes. Que veut dire moteur ditherme ? Un moteur ditherme échange de la chaleur avec deux sources. Représenter par un schéma de principe un moteur ditherme en faisant apparaître, les sources de chaleur, et le sens des échanges d'énergie. W : énergie échangée sous forme de travail ( énergie mécanique ) Qc ou Q : énergie thermique échangée par chaleur avec la source chaude à la température Tc ( ou T) Qf ou Q' : énergie thermique échangée par chaleur avec la source froide à la température Tf ( ou T') 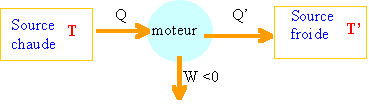L'efficacité énergétique d'une machine thermodynamique est le rapport entre l'énergie qui est récupérée utilement et celle qui a été dépensée pour la faire fonctionner. Exprimer l'efficacité énergétique d'un moteur ditherme en fonction de Qc et Qf. Au cours d'un cycle le fluide reçoit le travail W, cède la chaleur Qf  à la source froide et prend la chaleur Qc à lasource chaude. Au cours de ce cycle l'énergie interne du fluide est nulle : W + Qf + Qc= 0 avec Qc > 0 ; W et Qf <0 ; W = - Qf - Qc (1) efficacité énergétique h = |W| / Qc = |- Qf - Qc| / Qc. Quelle est l'expression de l'efficacité énergétique maximale nmax du moteur ditherme dont le fonctionnement est décrit par le cycle de Carnot. Le second principe s'écrit : Qf / Tf + Qc / Tc = 0 dans le cas de la réversibilité. Qf = -Qc Tf / Tc . Repport dans (1) : W= Qc [ Tf / Tc -1] nmax = 1-Tf / Tc. Le cycle d'une machine thermodynamique est généralement modèlisé par des transformations élémentaires. Donner les définitions succinte des expressions suivantes : isochore : transformation s'effectuant à volume constant. isobare : transformation s'effectuant à pression constante. isotherme : transformation  s'effectuant à température constante. isentropique : pas de variation d'entropie du système. adiabatique : pas d'échange thermique entre le système et le milieu extérieur. Etude d'un moteur de Stirling. Le moteur de Stirling est un système fermé : le gaz est confiné dans le système et aucune combustion n'a lieu à l'intérieur du moteur. 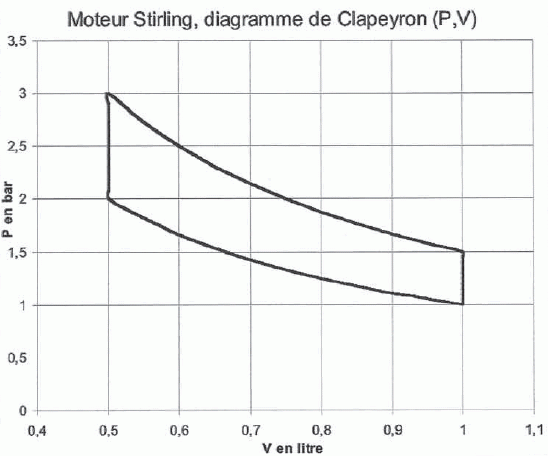Le moteur échange du travail W avec le milieu extérieur et, par conduction thermique, de l'énergie thermique avec les sources chaude et froide. On suppose que le gaz contenu dans la machine peut être considéré comme parfait. Le fonctionnement du moteur de Stirling est généralement modélisé par un cycle comportant  quatre transformations supposées réversibles représentées dans le diagramme (P, V ) ci-dessous.   Compression isotherme 1 --> 2 à la température Tf de la source froide. On passe du volume V1 au volume V2 tel que V1 > V2. Le gaz échange de l'énergie thermique par chaleur avec la source froide. Chauffage isochore 2--> 3 jusqu'à la température Tc de la source chaude. Détente isotherme 3 -->4 à la température Tc jusqu'au volume initial. Le gaz échange de l'énergie thermique par chaleur avec la source chaude. Refroidissement isochore 4 --> 1 jusqu'à la température Tf. On notera :  n : quantité de matière en mole du gaz parfait. R = 8,31 J K-1 mol-1. Cv : capacité thermique molaire à volume constant du gaz ; Cv = 21 J K-1 mol-1. W12, W23, W34, W41 : les échanges d'énergie par travail au cours des transformations 1-->2, 2-->3, 3-->4 et 4-->1. Q12, Q23, Q34, Q41 : les échanges d'énergie par chaleur au cours de ces mêmes transformations. A quoi correspond l'aire du cycle dans les coordonnées de Clapeyron ? L'aire du cycle correpond au travail ( en valeur absolue ) échangé par le système avec le milieu extérieur. Donner l'expression de la relation P =f(V) en fonction de Tf, n et R au cours de la compression isotherme  1--> 2. P V =P1V1 = P2V2 = nRTf = constante. Compléter le tableau ci-dessous en explicitant les calculs. état 1 état 2 état 3 état 4 T(K) 300 300 450 450 V (m3) 1,00 10-3 5,0 10-4 5,0 10-4 1,00 10-3 P(Pa) 100 103 200 103 300 103 150 103 Compression isotherme 1-->2 ; détente isotherme 3-->4. Chaufage isochore 2-->3 ; refroidissement isochore 4 --> 1. n = P1 V1 / (RT1) = 100 103*1,00 10-3 /(8,31*300) =4,0112 10-2 mol. P2 = nRT2/ V2 =4,0112 10-2 *8,31 *300 / 5,0 10-4 =2,0 105 Pa. P3 = nRT3/ V3 =4,0112 10-2 *8,31 *450 / 5,0 10-4 =3,0 105 Pa. P4 = nRT4/ V4 =4,0112 10-2 *8,31 *450 / 1,0 10-3 =1,5 105 Pa. Déterminer pour la compression isotherme, l'expression du travail W12 en fonction de V1, V2, Tf, n et R. 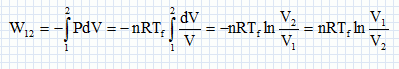Quelle est la variation d'énergie interne DU12 pour cette dernière transformation ?  En déduire l'expression de la quantité d'énergie échangée par chaleur Q12 avec la source froide en fonction de V1, V2, Tf, n et R.. L'énergie d'un gaz parfait ne dépend que de la température. Au cours d'une transformation isotherme, l'énergie interne du gaz parfait ne varie pas. DU12  = 0 ; DU12 =W12 +Q12 d'où Q12 = -W12.   Calculer les travaux W23 et W41 effectués pendant les transformations isochores. Ces travaux sont nuls, les transformations étant isochores. Etude de l'efficacité énergétique du moteur de Stirling. On montre que l'énergie fournie sous forme de travail lors d'un cycle a pour expression : Wmec = nR(Tc-Tf) ln(V2/V1). Dans le cas d'un fonctionnement idéal, l'énergie thermique transférée par chaleur au système pendant la phase de chauffage isochore 2 -->3  est entièrement récupérée durant la phase de refroidissement isochore 4--> 1 grâce à un échangeur thermique appelé régénérateur ou économiseur. On peut alors considérer que l'énergie thermique échangée par chaleur Qc n'est apportée au moteur que pendant la transformation 3-->4 et donc que Qc = Q34 = nRTc ln(V1/V2).  Montrer que le rendement du moteur Stirling peurt se mettre sous la forme h = 1-Tf/Tc.   Wmec = -nR(Tc-Tf) ln(V1/V2) ; h = |Wmec |/ Qc = (Tc-Tf) / Tc  = 1-Tf / Tc.   Dans ce cas, calculer : Wmec =0,040 *8,31 *(450-300) ln0,5 =-34,56  ~ -35 J. h =1-300 / 450 =0,33. Q34  = nRTc ln(V1/V2) =0,040 *8,31 *450 ln2 =103,68  ~ 1,0 102 J. Q12  = -W12 = nRTf ln(V2/V1) = 0,040 *8,31 *300 ln0,5 =-69,12  ~ -69 J. Déterminer N, la fréquence de rotation du moteur en tr /s qui correspond à une puissance mécanique Pmec = 100 W. n cycles par seconde soit un travail égal à 34,56 N joules par seconde. 34,56 N = 100 ; N = 100/34,56 = 2,89 ~ 3 tr/s. Pour cette même puissance mécanique fournie, donner l'expression de la puissance thermique  Pthe qui doit traverser l'échangeur thermique entre le moteur et la source froide en fonction de N et Q41 , puis en fonction de n, Cv, T0 et Tf . Pthe = N Q41 ; DU41 = W41 +Q41 = n Cv (T1-T4) ; or W41  = 0  ; T1 = Tf  et T4 = Tc . Q41 = n Cv (Tf-Tc) ;  Pthe = N n Cv (Tf-Tc). Pthe = 2,89 *0,04 *21*(-150) = 364 W ~ - 3,6 102 W. Dans la réalité, l'hypothèse faite " récupérer totalement la quantité d'énergie échangée par chaleur  lors du  refroidissement isochore pour la restituer au cours du chauffage isochore", est en réalité impossible à réaliser  sur le plan pratique. Il faudrait pour cela que le  régénérateur ait une eficacité de 100 %. Certains moteur de Stirling comme celui représenté sur la figure ci dessous, ne possèdent pas de régénérateu et ne récupèrent donc rien. Calculer l'efficacité énergétique d'un moteur sans régénérateur dont le fonctionnement est modélisé par le même diagrmme PV que précédemment. On prendra Q41 = 125 J. DU23 = W23 +Q23 = n Cv (T3-T2) ; or W23  = 0  ; T2 = Tf  et T3 = Tc . Q23 = n Cv (Tc-Tf) = 0,04*21*150 = 126 J. Qc =Q23  + Q34 = 126 + 103,68 =229,68 J ; Wmec =-34,56  J  h = |W| / Qc =34,56 / 229,68 = 0,15.

menu