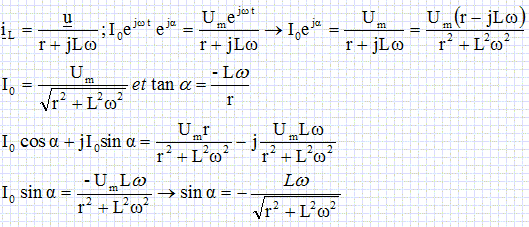Accélérateurs  de Van de Graaff, de Wilderöe, cavités résonantes : concours Capes  2011 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

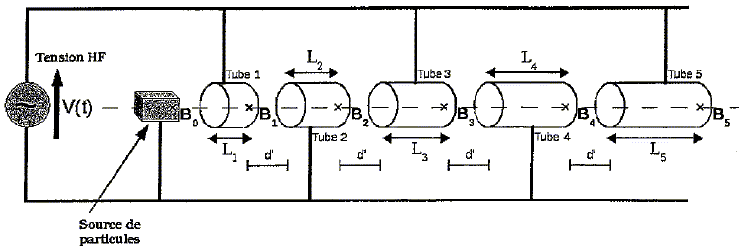
Historiquement, l'accélérateur de Van de Graaff est un des premiers à avoir été utilisé. Il constitue la partie droite du schéma ci-dessous : 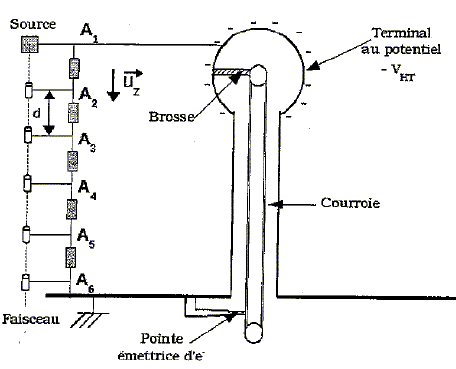Des électrons sont arrachés à la pointe par la courroie et transportés jusqu'à la brosse, ils sont ensuite accumulés au niveau du terminal. Un système de résistance toutes égales à R relient le terminal à la pointe. On choisit le potentiel nul au niveau de la pointe. Soit V= -VHT le potentiel du terminal, c'est également le potentiel de la source VA1 = -VHT. L'accélérateur est situé sur la gauche du schéma. Au niveau de la source, des électrons sont produits et ont le potentiel VA1. Ils sont accélérés en direction du tube cylindrique creux porté au potentiel VA2, puis vers les différents tubes portés aux potentiels VAi pour i entier appatenant à [3 ; 6 ]. On note d la distance entre chaque tube. On supposera que la longueur d'un tube est négligeable devant d. Décrire une expérience simple illustrant l'apparition de charges sur un isolant. Production de charge par frottement : - la laine frottée avec le verre  : résultat : le verre se charge positivement la laine négativement. - la laine frottée avec l'ébonite  : résultat : la laine se charge positivement l'ébonite négativement.  Comment mettre en évidence expérimentalement la répulsion entre charges de même signe. Charger deux petits pendules ( petite boule métallique + fil isolant ) par contact avec un baton d'ébonite frottés avec du verre. Rapprocher les pendules, ceux-ci s'écartent l'un de l'autre. Accélérateur de Van de Graaff. Exprimer les valeurs des potentiels électriques aux points A6, A5, A4, A2 et A1. -VHT = 5 R i ; i =-VHT / 5 ; VA6 = 0 ; VA5 = R i = -VHT / 5 ; VA4 = 2R i = -0,4VHT  ; VA3 = 3R i = -0,64VHT  ; VA2 = 4R i = -0,8VHT  ; VA1 = 5R i = -VHT. On note d la distance entre deux points sucessifs et on admet que le champ électrique est uniforme. Exprimer ce champ électrique. 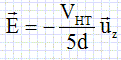Les électrons  ( de charge -e, de masse m ) sont produits au niveau de la source sans vitesse initiale. Exprimer leur énergie cinétique Eci dans le tube relié au point Ai en fonction de e et de VHT.  Le poids  est négligeable devant la force électrique. Le théorème de l'énergie cinétique s'écrit : Eci-0 = -eVAi ; Eci = e i / 5 VHT avec i = 1, 2, 3, 4, 5. A.N : VHT = 100 103 V. Ec6 = 1,60 10-19 * 100 103 =1,60 10-14 J. Pourquoi ce type de générateur est-il dangereux si on cherche à obtenir des énergies cinétiques importantes ? La tension électrique |VHT | doit être de plus en plus grande : risque de claquage si on travaille dans l'air. Accélérateur linéaire de protons de Wilderöe. Pour atteindre des tensions supérieures, on utilise des accélérateurs linéaires fonctionnant avec un générateur sinusoïdal à haute fréquence ( HF). Les particules accélérées sont maintenant des protons. Les protons produits au niveau de la source, traversent des tubes de cuivre reliés à l'une ou à l'autre des bornes du générateur.   La tension délivrée par le générateur est V(t) = -Vmax sin ( w t + F) avec Vmax positif. On note T la période du signal. Les tubes sont distants de d'. A l'intérieur de chaque tube, le champ électrique est nul, il est uniforme entre deux tubes consécutifs. On supposera que d' est suffisamment faible, pour que l'on puisse considérer que le proton voit un champ électrique indépendant du temps, entre deux tubes consécutifs. Le point B0 est placé à la sortie de la source, les différents points Bi sont placés à la sortie des tubes i. On note Li la longueur du tube i. Les seules forces considérées sont les forces électriques. L'étude est faite dans le cadre de la mécanique classique. Variations temporelles. Exprimer T en fonction de w. w = 2 p f = 2 p / T ; T = 2 p / w. Représenter les vecteurs champs électriques, à la date t=0, aux points B0, B1, B2, B3, B4, B5. On prendra F compis entre 0 et p. ( on choisit F = 90° ). E0 = |V0 | / d' ; E1 = |V0 | /d' ; E2 = |V0 | / d' ; E3 = |V0 | / d' ; E4 = |V0 | / d' ; E5 = |V0 | / d' avec |V0 | = |Vmax | sin F. Même question à la date t = ½T. 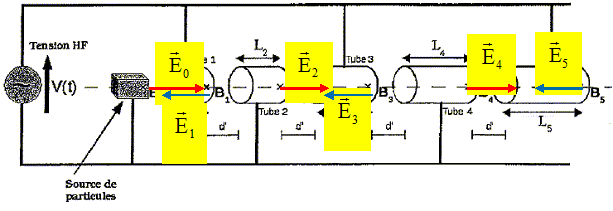V(½T) = -Vmax sin (p+ F ) =  Vmax sin ( F ) . Les champs électriques ont la même norme qu ci-dessus, mais ont changé de sens. Condition d'accélération. On note vi la vitesse au point Bi. A quelle condition les protons sont-ils toujours accélérés ? Au point Bi+1, le champ électrique doit avoir le même sens qu'au point Bi et sa valeur doit être maximum. La durée du parcours Li doit être égale à la demi-période ½T. Si cette condition est respectée, représenter en fonction du temps l'allure de la vitesse des protons entre les points B0 et B5. v0 ~ 0 ; à chaque passage entre deux tubes, l'énergie cinétique des protons augmente de la quantité e Vmax pour une accélération maximale. ½mpv12 = e Vmax  ; v1 = (2e Vmax /mp  )½ ; ½mpv22 - ½mpv12 = e Vmax  ; v2 = (v12 +2e Vmax /mp  )½ =(4e Vmax /mp  )½ = 2½v1 ;   vi =(2 i e Vmax /mp  )½ = i½v1. La vitesse reste constante à l'intérieur des tubes ; la vitesse croît linéairement entre les tubes, l'accélération étant constante. 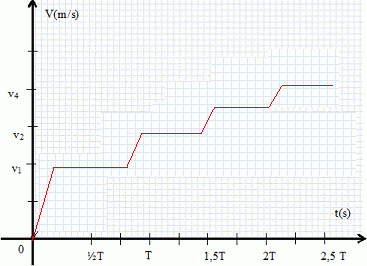Les tubes ont-ils tous la même longueur, pour une accélération optimale ? La durée du parcours de chaque tube est voisine de ½T et la vitesse des protons augmente : les tubes n'ont pas la même longueur. On s'intéresse à un proton placé en B0 sans vitesse initiale à t=0. Le générateur est synchronisé avec le mouvement de la particule pour l'accélérer à chaque Bi. On supposera que d' est suffisamment faible pour que l'on puisse négliger la durée de chaque phase d'accélération devant la durée du parcours dans les tubes. Exprimer Li en fonction de vi et T. Li = ½vi T. Pour quelle valeur de F, le proton est-il effectivement accéléré ? L'accélération est optimale si  à t =0, V(0) = -Vmax sin F = -Vmax.  F = ½p. V(0) doit être négatif pour qu'il y ait accélération donc F est compris entre 0 et 90°. Exprimer l'énergie cinétique de la particule en Bi en fonction de mp, Li et T. Ec1 =½mpv12 = ½mp (2L1/T)2. Ec2 =½mpv22 = ½mp (2L2/T)2 ; Eci =½mpvi2 = ½mp (2Li/T)2 . Pour une vitese proche de c, et une fréquence du GBF égale à 10 MHz, calculer la longueur d'un tube. T = 1/f = 1 / 107 =1,0 10-7 s. L = ½c T= 0,5 *3,0 108 *1,0 10-7 =15 m. Expliquer pourquoi ce type d'accélérateur provoque un regroupement des particules en paquets. 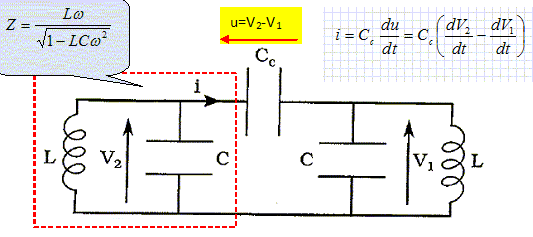Cavités résonnantes. Pour atteindre des énergies supérieures, en gardant une longueur de tubes raisonnable, il faut augmenter la fréquence du générateur. A haute fréquence, les tubes se comportent comme des antennes dipolaires et rayonnent énormément d'énergie. La solution, pour éviter ces pertes, consiste à enfermer les tubes dans une cavité résonante dont les parois réfléchissent le rayonnement. Les cavités, pour les ondes radio-fréquences ( RF), peuvent être modélisées par un circuit électrique simple. l'excitation est modélisée par un générateur idéal de tension. On se place en régime sinusoïdal forcé à la pulsation w et on adopte la notation complexe : u(t) = R[u(t)] et u(t) = Um exp(jwt). 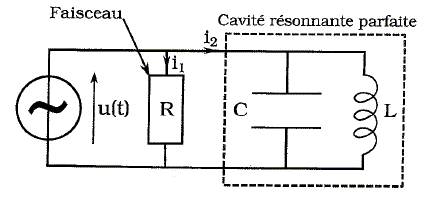Modèle électrique d'une cavité parfaite. Une cavité parfaite peut être modélisée par un condensateur de capacité C mis en parallèle avc une bobine d'inductance L. Le faisceau est modélisé par une résistance de charge R. Donner l'impédance complexe équivalente de la cavité résonante parfaite. 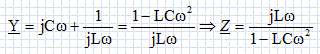Donner les expressions réelles du courant i1(t) traversant la résistance R et i2(t) traversant la cavité, en fonction de Um, R, L, C, w et t. u(t) =Ri1(t) ; i1(t) = Um / R cos (w t). u(t) =Z i2(t) ; i2(t) = Um exp(jwt) / Z. 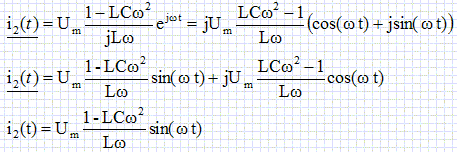Pour quelle valeur particulière w0 de w, i2(t) est-elle nulle ? w0 =(1/ (LC))½. Modèle d'une cavité réelle : 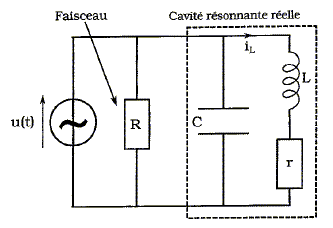Dans une cavité réelle, les courants surfaciques sur les bords de la cavité induisent des pertes. On modélise ces pertes par une résistance r placée en série avec la bobine. On note x = w / w0. Calculer l'impédance complexe équivalente de la cavité résonante réelle. On pose Q =Lw0 / r. 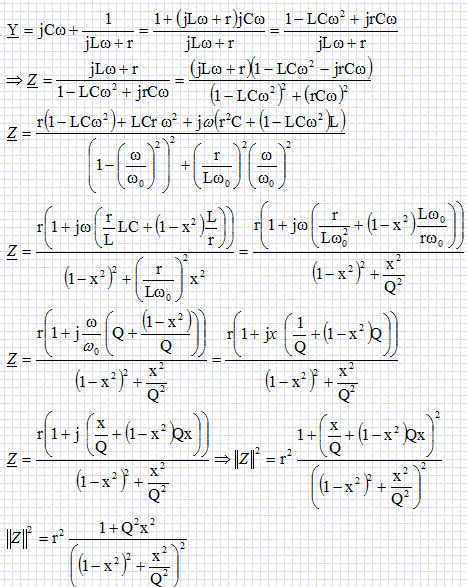Soit iL(t) =I0 cos (wt+a) le courant circulant dans la branche contenant la bobine et la résistance r. Exprimer I0, tan a, sin a en fonction de L, Um w et r. Dans la suite de l'énoncé, on se place dans une situation où Lw >> r. Que vaut a ? Que peut-on dire du courant circulant dans la bobine et de la tension aux bornes du condensateur ? sin a = -1 ; a = -90°. I0 = Um / (Lw) ; iL est en retard de 90) sur la tension u(t). La tension aux bornes du condensateur est u(t). On suppose que w = w0. En déduire une expression de l'énergie U totale stockée dans la cavité résonante en fonction de L et I02. énergie u = ½CUm2cos2(w0t) +½LI02sin2(w0t-90) ; or sin2(w0t-90) = cos2(w0t) ; I0 = Um / (Lw0) et CLw02=1. u = ½cos2(w0t) (CL2I02w02+LI02) = LI02cos2(w0t) ; <u> =U = ½ LI02. Exprimer la puissance moyenne P dissipée dans r.. Montrer que l'on retrouve la relation Q = w0U/ P. p = r iL2(t) = rI02sin2(w0t-90) = rI02 cos2(w0t) ; P=<p> =½rI02. w0U/ P =w0½ LI02 /( ½rI02) =Lw0 / r = Q. Lorsque la cavité est à température ambiante, Q = 3,00 104. A la température de 4 K, Q = 1010 et la puissance dissipée vaut 16 W. Que vaudrait la puissance dissipée dans une cavité fonctionnant à température ambiante et ayant la même énergie stockée ? P = w0U/Q avec w0U =PQ = 16 1010. Pambiant = 16 1010/  3,00 104~5 106 W. La puissance dissipée dans r est énorme à température ambiante, d'où l'intérêt  d'utiliser des cavités supraconductrices à 4 K. On pose D = Cc/C ; w0 =(1/ (LC))½ ; x = w / w0. En déduire le système d'équations différentielles couplées vérifiées par V1 et V2. i =V1 / Z =V1 (1-x2)/ (jLw)  ; i = Cc(jwV2-jwV1). V1 (1-x2) = Cc(jwV2-jwV1)(jLw) = -w2 Cc(V2-V1) ; V1 ((1-x2) -w2 LCCc/C)+w2 LCCc/CV2=0. V1 ((1-x2) -Dx2)+Dx2V2=0. De même : i = -V2 / Z =-V2 (1-x2)/ (jLw)  ; -V2 (1-x2) = Cc(jwV2-jwV1)(jLw) = -w2 Cc(V2-V1) ; V2 (-(1-x2) +w2 LCCc/C)-w2 LCCc/CV1=0. -Dx2V1+ V2 (-(1-x2) +Dx2)=0 ; Dx2V1+ V2 ((1-x2) -Dx2)=0 ; En régime sinusoïdal forcé, montrer que le système d'équations revient à résoudre : (1-(1+D)x2)2 -D2x4=0. Le discriminant du système doit être nul. Trouver les deux pulsations propres et commenter. (1-(1+D)x2+Dx2) (1-(1+D)x2-Dx2) = 0 ; (1-x2) (1-x2-2Dx2)=0 x =1 soit w = w0 et x =1/(1+2D)½soit w = w0/(1+2D)½. Si le système comprend N cavités couplées, on trouvera N+1 modes propres. On  étudie une cavité, fonctionnant avec une source radio-fréquence délivrant la tension :V(t) =-Vmax sin ( 2pfRF t+F) ; fRF = 700 MHz , Vmax =1,00 106 V. calculer la période du champ radio-fréquence. T = 1/ fRF =1 / 7,00 108 = 1,4286 10-9 ~ 1,43 10-9 s. Calculer la longueur d'un tube Li. ( vi = 0,65 c). Li = ½ vi T= 0,5 *0,65*3,0 108 * 1,4286 10-9 =0,14 m. Dans le cas des cavités, la longueur d'un tube correspond à la distance entre deux cellules. Cette grandeur est indépendante de i et sera notée Lcellule. On admet que, dans une cavité, une particule entrant  avec un déphasage F par rapport au champ électrique subit le même champ E tout au long de son déplacement, on a : E =Vmax sin F /Lcellule. Montrer que l'énergie acquise par la particule dans la cavité est alors DU= Ncell eVmax sin F. ( Ncell = nombre de cellules dans la cavité ). E étant constant et le déplacement dans la cavité étant NcellLcellule, alors DU= E Ncell Lcellule, Energie acquise : eDU =  Ncell eVmax sin F. A.N : Ncell = 5 ; F = 90°. Energie = 5*1,6 10-19*1,00 106 =8 10-13 J ou 8 10-13 /1,6 10-19 =5 106 eV = 5 MeV.

menu