Etude générale du LHC : énergie et vitesse, nombre de collisions : concours Capes  2011 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

A l'heure actuelle, notre compréhension de l'Univers est très incomplète, cependant le modèle standard des particules et des forces propose une description précise de la physique des particules. Ce modèle prédictif n'a pour l'heure jamais été mis en défaut, il ne donne cependant pas de réponse à de nombreuses questions. les expériences du LHC pourront peut-être nous éclairer. Boson de Higgs. Un des premiers objectifs du LHC est de découvrir une particule associée au champ de Higgs :le boson. L'interaction des autres particules avec ce champ serait à l'origine de leur masse. Plus l'interaction est importante avec ce champ, plus la particule est massive. ce mécanisme pourrait expliquer les grosses différences de masse observées entre particules fondamentales. On appelle particule élémentaire tout constituant fondamental ne résultant pas de l'interaction d'autres particules plus petites. Donner le nom d'une particule élémentaire dont la masse est considérée comme nulle dans l'état actuel des connaissances. Le photon est une particule élémentaire de masse nulle. Donner également le nom de deux particules élémentaires de masse non nulle. L'électron, les quarks ont une masse non nulle. Unification des interactions. En 1967, Weinberg et salam parviennent à unifier en une seule théorie l'interaction électromagnétique et l'interaction nucléaire faible : c'est la théorie électro-faible qui  leur vaudra le prix Nobel en 1979, conjointement avec Glashow. Citer les quatre interactions fondamentales. La gravitation ; l'interaction nucléaire faible ; l'interaction électromagnétique ; l'interaction nucléaire forte. La supersymétrie est une théorie qui pourrait faciliter l'unification des interactions fondamentales. Le LHC va traquer des particules supersymétriques. Masse manquante et antimatière. Les observations cosmologiques ont montré que l'ensemble de la matière visible ne constitue que 4 % de la masse de l'univers. Le LHC est à la recherche de particules responsables de la matière noire et de l'énergie sombre. On cherche également à comprendre le déséquilibre de l'univers entre matière et anti-matière. L'électron a-t-il une anti-particule ? Si oui, quelles sont sa charge et sa date approximative de découverte ? A chaque type de particule correspond une anti-particule. A l'électron est associé l'anti-particule nommée positon, découvet en 1932 : sa charge est positive, égale à la charge élémentaire. Energie et vitesse d'une particule. Les accélérateurs sont construits dans le but d'étudier des phénomènes, souvent rares, dont la probabilité varie avec l'énergie de collision. C'est pourquoi les paramètres le plus importants sont l'énergie du faisceau et le nombre de collisions. On note E, l'énergie relativiste d'un proton, v sa vitesse et mp sa masse. 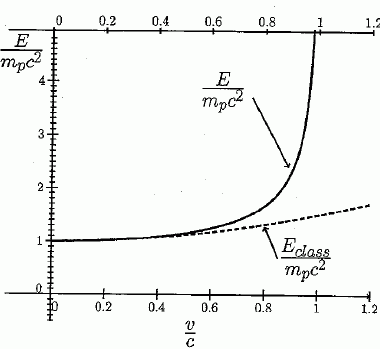On note E0 l'énergie du proton au repos, également appelée énergie de masse.   Soit Eclass= E0+½mpv2 que l'on nommera l'énergie classique de la particule. Sur le même graphe est représenté en pointillés, Eclass/ (mpc2). Particule au repos. A l'aide du graphe, donner l'expression de E0 en fonction de mp et c2. Quel est le nom de cette relation ? De quand date-t-elle ? Ordonnée à l'origine ( v = 0) du tracé en pointillés : Eclass / (mpc2) = 1 ; Eclass = mpc2. Eclass= E0+½mpv2  ; soit pour v = 0 : Eclass= E0 = mpc2. Cette relation, formulée en 1905, exprime l'équivalence entre la masse et l'énergie. Calculer en eV, l'énergie de masse d'un proton. mp =1,67 10-27 kg ; c = 3,00 108 m/s. E = mpc2 =1,67 10-27 *9 1016 =1,503 10-10 J = 1,503 10-10 /1,60 10-19 eV =9,39 108 eV. Justifier alors que la masse d'un proton mp =1,67 10-27 kg puisse également s'écrire mp=939 MeV /c2. mp =E / c2 =9,39 108 eV/c2 = 939 MeV/c2. En vous aidant du graphe, justifier pourquoi il est impossible d'accélérer le proton jusqu'à la vitesse de la lumière. E / mpc2 tend vers l'infini quand la vitesse du proton tend vers la vitesse de la lumière.  Pour tendre vers la célérité de la lumière (sans pouvoir l'atteindre), il faut fournir une énergie tendant vers l'infini, ce qui est techniquement impossible.   Donner l'intervalle de vitesse dans lequel le rapport (E-Eclass) / E est approximativement inférieur à 10 %. 1-Eclass / E < 0,1 ; Eclass > 0,9 E avec Eclass  = mpc2+½mpv2 ; E = g mpc2 et  g =(1-v2/c2)-½ . mpc2+½mpv2 >0,9 g mpc2 ; c2+½v2 >0,9 g c2 ; 1+0,5 v2/c2 >0,9 g ; on pose ß2 =v2/c2 . 1+0,5ß2 >0,9 (1-ß2)-½  ; (1+0,5ß2 )2 >0,81(1-ß2)-1  ; (1+0,5ß2 )2 (1-ß2) >0,81 ; (1 +ß2 +0,25ß4 ) (1-ß2) >0,81 ; 1 +ß2 +0,25ß4 - ß2 -ß4 -0,25ß6  >0,81 ; +0,75ß4 +0,25ß6  < 0,19 ; ß <0,683 ; v/c <0,683 ;  v < 0,68 c. L'expression relativiste d'une particule est : E = g mc2 avec g = (1-v2/c2)-½. Montrer que si v << c alors E ~Eclass. (1-v2/c2)-½ ~ 1+0,5v2/c2 ; E ~(1+0,5v2/c2) mc2 = mc2 +0,5 mv2 ~Eclass. Calculer en MeV les énergies du proton : Einjection, à l'injection dans le LHC pour v =  0,999 997 828 c Emax,  pour v = 0,999 999 991 c. g = (1-0,999 997 8282)-½ =479,8 ; Einjection = 479,8 *1,67 10-27 *9 1016 =7,21 10-8 J =7,21 10-8 /1,6 10-13 = 4,51 105 MeV. .g = (1-0,999 999 9912)-½ =7453 ; Einjection = 7453 *1,67 10-27 *9 1016 =1,12 10-6 J =1,12 10-6 /1,6 10-13 = 7,00 106 MeV. Expliquer alors pourquoi, en physique des particules, on se réfère généralement à l'énergie de la particule et non à sa vitesse. Les particules ont pratiquement toute la même vitesse, très proche de la vitesse de la lumière dans le vide. Par contre une très faible augmentation de vitesse ( moins de 1 /10000è) peut  conduire à une énergie 10 fois plus grande. ( voir calcul ci-dessus ). Nombre de collisions. Au LHC, deux tubes circulaires différents contiennent des protons tournant dans des sens opposés. A l'intérieur de chacun des tubes, les protons se propagent en groupes ; ces groupes portent le nom de paquets. Dans chaque tube,on compte approximativement NP =2810 paquets répartis sur toute la circonférence D du LHC. Chaque paquet contient environ N = 1011 protons. Pour les applications numériques la vitesse des protons sera prise égale à c et D égale à 26,6 km. On se place dans un référentiel lié au sol. En supposant les paquets régulièrement espacés, exprimer puis calculer la distance moyenne dmoy séparant deux paquets dans le même tube. dmoy =  D / NP =2,66 104 / 2810 = 9,47 m. Exprimer puis calculer la durée moyenne Dtmoy séparant le passage de deux paquets d'un même tube pour un observateur du LHC. Dtmoy = dmoy / c = 9,4662 / 3 108 =3,1554 10-8 ~3,16 10-8 s. L'accélérateur est réglé de manière à ce que les paquets isus de chacun des tubes se rencontrent toujours au même point appelé point de collision. Calculer la fréquence f des collisions observées en ce point. f = 1/Dtmoy =1 /3,1554 10-8 =3,17 107 Hz. Il existe au LHC plusieurs points de collision. Le texte ci-dessous correspond à un exercice donné à une classe de terminale de lycée. Proposer une correction succincte de celui-ci. Au bowling, Pierre lance en ligne droite, "sans effet", une boule de rayon R sur une quille cylindrique de rayon r. On a R = 10,8 cm et r = 6,00 cm et D0 =1,05 m. On note d la distance entre le centre de la quille et celui de la boule. Quelle est la trajectoire de la boule ? La boule a une trajectoire rectiligne. Indiquer la valeur maximale de d pour que Pierre atteigne la cible. dmax =R+r =10,8 +6,00 =16,8 cm. La quille est posée sur la piste de largeur D0. On suppose que la surface de contact entre la quille et le sol est entièrement contenu sur la piste. Si Pierre ne sait pas où se trouve la quille,  combien doit-il effectuer de jets au minimum pour être sûr de l'atteindre ? Le centre de gravité de la quille est compris entre 0,06 m et 0,99 m, d'où : (D0 -2r)/ (2dmax )=0,93 / 0,336 =2,768 soit 3 jets. En déduire la probabilité de toucher la quille pour un jet quelconque. p =1/3 = 0,333. Ce résultat serait-il modifier si la quille avait un mouvement rectiligne parallèle à celui de la boule mais en sens opposé ?  Non, le calcul précédent est indépendant du sens des vitesses. En s'inspirant de l'exercice précédent,nous allons proposer un modèle permettant d'évaluer la probabilité qu'à un proton d'entrer en collision avec un autre proton venant en sens inverse. Diamètre du faisceau, supposé cylindrique, au moment de la collision : D1 =16,0 µm. Le proton est considéré comme une sphère de rayon R1 = 0,875 10-15 m. Chaque paquet contient N = 1011 protons. Montrer qu'un proton entre en collision avec un proton venant en sens inverse si son centre de gravité se trouve dans un cylindre de rayon 2R1 centré sur le premier proton. Pour qu'il y ait collision ,la distance maximale entre les centres de gravité des deux protons est : d = R1+R1 = 2 R1. En déduire que la probabilité p qu'à un proton d'entrer en collision avec un proton venant en sens inverse est p = (4R1 / D1)2. Le nombre de cas favorables à une collision est proportionnel à  la surface cylindrique de rayon 2R1 ; le nombre de cas possibles est proportionnel à la surface cylindrique de rayon ½D1. p = p(2R1)2 / (p (0,5 D1)2) = (4R1 / D1)2. En déduire le nombre de collisions lorsque deux paquets se croisent. Ncol =N2 p = N (4R1 / D1)2  = 1022 * (4*0,875 10-15 / 16,0 10-6)2  =4,785 102. Nombre de collisions en une seconde : 4,785 102 * f = 4,785 102 * 3,17 107 = 1,52 1010. Ce calcul surévalue le nombre de collisions car le LHC génère environ 600 millions (  6 108) collisions par seconde. Commenter. Ce modèle doit être amélioré : il faudrait prendre en compte les interactions entre protons ; le proton n'est pas forcément sphérique. Energie électrique au LHC. On considère les composants électriques suivants : ampoule électrique à économie d'énergie ; lave linge ; téléphone portable. Indiquer s'ils sont alimentés par un courant continu ou alternatif, donner l'ordre de grandeur de la puissance électrique qu'ils consomment, de la tension à leurs bornes ( donner la tension eficace en alternatif ). courant tension puissance lave linge alternatif 220 V 2 à 3 kW ampoule à économie d'énergie alternatif 220 V 10 à 20 W portable continu quelques volts 0,1 à 0,2 W Le fonctionnement du LHC est discontinu, cependant on estime qu'il fonctionne l'équivalent de 270 jours par an, 24 heures sur 24 en consommant la puissance moyenne de 120 MW. Donner l'énergie qu'il consomme annuellement en kWh puis en joules. 270 jours = 270*24*3600 s = 2,33 107 s. 120 MW = 1,2 108 W.  Energie  =1,2 108 *2,33 107 = 2,8 1015 J. ou 270 jours = 270*24 heures =6,48 103 h ; 120 MW = 1,2 105 kW. Energie = 6,48 103 *1,2 105  =7,8 108 kWh. Justifier que cela correspond à peu près à l'énergie annuelle consommée par les ménages du canton de Genève. On donne : canton de Genève : 430 000 habitants ; consommation moyenne annuelle par habitant : 2 MWh. 430 000* 2000 =8,6 108 kWh. Lors du fonctionnement nominal du LHC, on dispose, dans chaque faisceau, d'environ N1 = 2,81 1014 protons ayant chacun une énergie E1 = 7,00 TeV. Calculer en joule, l'énergie de chaque faisceau. E1 = 7,00  1012 eV. E = E1 N1 = 7,00  1012 *2,81 1014 = 1,97 1027 eV. 1,97 1027 *1,60 10-19 =3,15 108 J. Comparer à l'énergie cinétique d'un TGV de 400 tonnes lancé à 140 km/h. v =140/3,6 =38,9 m/s : 400 t = 4,00 105 kg. Ec = ½mv2 =0,5 *4,00 105 *38,92 =3,02 108 J. Nombre d'informations à traiter. On cherche à connaître le débit de données issues des quatre expériences du LHC. Ce débit s'exprime en octet par seconde ( o / s). Voici un texte issu d'un journal scientifique : " le flux de données provenant de quatre expériences du LHC pendant les 270 jours de fonctionnement annuel, représente l'équivalent d'une pile de CD-ROM haute de 20 km ". Pourquoi l'expression "quantité de données" serait-elle plus correcte que " flux de données". Les données sont recueillies puis " stockées" en vue d'une exploitation futur. le mot "flux" laisse penser à la transmission de données d'un point à un autre  et non pas au stockage. Evaluer et calculer le débit de données DLHC généré au LHC en utilisant les données suivantes : Hauteur d'une pile de 100 CD-ROM : 12 cm ; capacité de stockage d'un CD-ROM : 700 106 octets. 100 * 20 000 / 0,12 = 1,6667 107 CD-ROM 1,6667 107 *700 106 =1,1666 1016 octets. 270 jours = 2,33 107 secondes Débit DLHC =1,1666 1016 /2,33 107 =5,00 108 o/s. .

menu