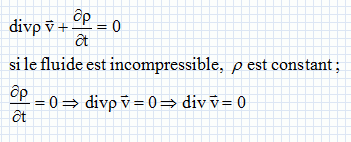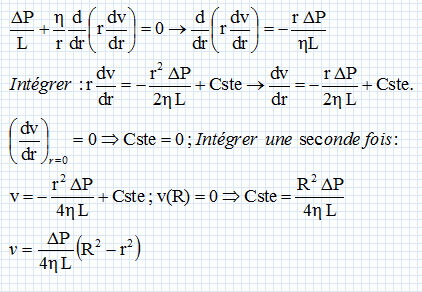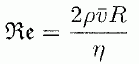Ecoulement d'eau à travers un nanotube de carbone : concours Agrégation  2009 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

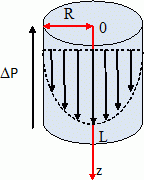
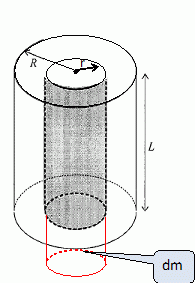
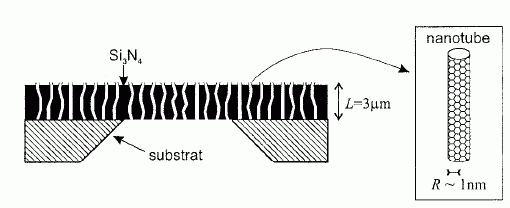Des expériences publiées récemment ont permis la mesure de l'écoulement d'eau à travers une membrane poreuse de nitrure de silicium dont les pores sont des nanotubes de carbone alignés les uns avec les autres. Le diamètre des nanotubes est compris entre 1,3 et 2 nm tandis que l'épaisseur de la membrane est 3 µm. La densité surfacique de nanotubes est 0,25 cm-2. On cherche ici à comparer les résultats de ces mesures à un modèle hydrodynamique simple. Ecoulement de Poiseuille. Pour modéliser le transfert de liquide à travers un nanotube de carbone, on considère l'écoulement dit de Poiseuille, d'un fluide de masse volumique r, de viscosité h à travers un cylindre de rayon R. On s'interesse à l'écoulement stationnaire induit par  une différence de pression DP sur une longueur L du tube. On utilise les coordonnées cylindriques r, q et z. L'origine z=0 de l'axe des z est notée O. On note P(M) la pression au point M et on pose P(z=0) - P(z=L) = DP. On cherche le champ des vitesses du fluide sous la forme 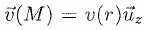. On néglige les effets de la pesanteur. On rappelle l'expression de la divergence en coordonnées cylindriques : 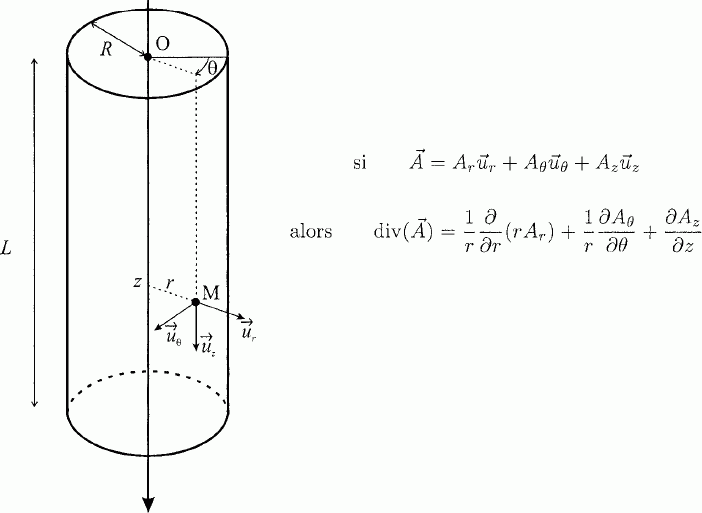Ecrire l'expression mocale traduisant la conservation de la masse. 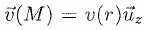Les débits volumiques entrant et sortant d'une surface fermée sont égaux.     Un champ de vitesse de la forme vérifie t-il cette équation ? A quelle condition peut-on considérer le fluide incompressible ? Un champ de vitesse de la forme ci-dessus vérifie cette équation. Un fluide est dit incompressible lorsque son volume reste constant sous l'action d'une pression extérieure. Ceci est vrai dans le cas où le nombre de Mach ( vitesse locale du fluide / vitesse du son dans ce fluide ) de l'écoulement est faible. Dans la suite on suppose cette condition réalisée. On considère l'élément de fluide représenté ci-dessous. On rappelle l'expression de la force de viscosité exercée sur cet élément par le fluide situé entre 0 et r. 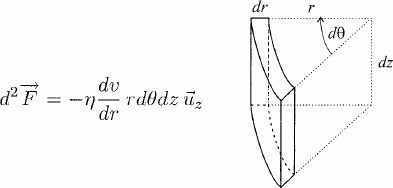Quelle est l'origine microscopique de la force de viscosité ? Par son mouvement, un fluide transporte de la quantité de mouvement Les forces de viscosité transfèrent de la quantité de mouvement des régions où la vitesse est grande vers les régions où la vitesse est plus faible. Calculer la résultante des forces de viscosité qui s'exercent sur l'élément du fluide. 1 : force exercée par le fluide compris entre 0 et r ; 2 : force exercée par le fluide situé au delà de r+dr. L'équation dite de Navier-Stokes, qui régit le champ des vitesses du fluide en régime stationnaire et en géométrie cylindrique s'écrit : 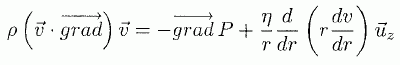Intpréter chacun des termes de cette équation. Il s’agit de l'écriture de l’équation fondamentale de la dynamique pour la particule fluide de masse dm = r dV. Le terme 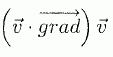est une accélération. A droite le terme en gradient représent les forces de pression et le terme suivant représente les forces de viscosité. Dans la géométrie considérée : 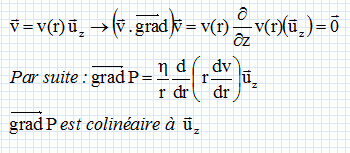En conséquence P ne dépend que de z. De plus v ne dépend que de r, donc le gradient de pression est indépendant de z. 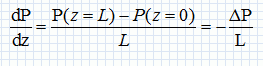La pression est une fonction linéaire décroissante  de z. En utilisant les conditions aux limites au centre et sur le bord du tube, montrer que :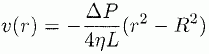. Représenter le profil de la vitesse dans le tube. Débit d'écoulement volumique, noté D : un débit volumique(m3 s-1) est une section (m2) fois une vitesse (m / s). 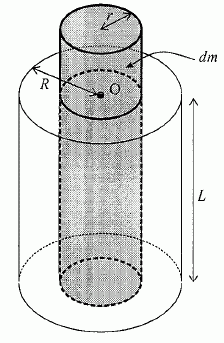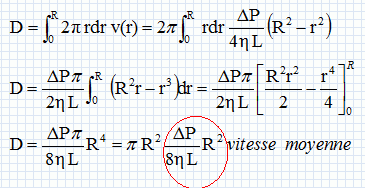En comparant les débits induits par un même gradient de pression dans un tube de rayon R et dans 100 tubes de rayon R/10, commenter la dépendance de R et D. Le débit volumique est proportionnel au rayon du tube à la puissance quatre, c'est à dire au carré de la section. Pour une même section, le débit sera donc 100 fois plus petit dans 100 tubes de rayon 0,1 R, par rapport au débit dans un seul tube de rayon R. Quelle est l'origine physique de cecomportement très différent de celui observé dans le transport du courant électrique ? La vitesse du fluide est nulle  sur les bords du tube, ce n'est pas le cas pour le courant électrique. En conséquence, si on diminue le diamètre du tube, le gradient de vitesse du fluide et les forces de viscosité augment fortement. On se propose de retrouver rapidement les résultats précédents en faisant le bilan  des forces qui s'exercent sur le système fermé constitué du fluide à l'intérieur d'un cylindre de rayon r < R à l'instant t et de masse dm de fluide qui pénètre entre t et t+dt. Représenter le système fermé à la date t+dt. date t date t+dt On note 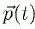la quantité de mouvement du système fermé à l'instant t et on suppose que la pression est uniforme sur une section droite du cylindre. Montrer que 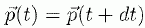. Le champ de vitesse ne dépend que du rayon r ; ce champ est indépendant de z et du temps. Quelles sont les forces qui s'exercent sur le système fermé considéré entre t et t+dt ? Somme des forces de pression  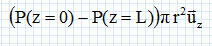: Forces de viscosité de la part du reste du fluide : 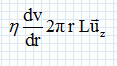Ecrire le théorème de la résultante cinétique appliqué au système : 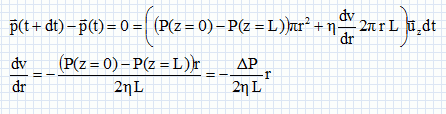On définit le nombre de Reynolds de l'écoulement par : Quelle est la signification physique de ce nombre ? Dans quelle limite les calculs faits ci-dessus sont-ils pertinents ? Ce nombre est sans dimension. Il permet de caractériser le type d'écoulement, c'est à dire l'importance du transfert de quantité de mouvement par convection et diffusion. A un faible nombre de Reynolds, correspond un écoulement ou  la diffusion domine. A un faible nombre de Reynolds, correspond un écoulement ou  la convection domine. Les calculs ci-dessus sont faits pour un écoulement à faible nombre de Reynolds. Analyse de résultats expérimentaux. En supposant un écoulement de type Poiseuille, évaluer le débit volumique d'eau D à travers un nanotube de carbone de rayon R =1 nm, de longueur l = 3 µm pour une différence de pression de 1 bar. Viscosité de l'eau h = 10-3 Pa s. D = 3,14 R4DP / (8 hL)=3,14 10-36 105 / (8 10-3 *3 10-6) =1,3 10-23 m3 /s. Evaluer la distance moyenne entre molécules d'eau dans l'eau liquide. Dans 18 g ou18 mL d'eau il y a 6,02 1023 molécules. Nombre de molécules d'eau par unité de volume : n = 6,02 1023 / 18 10-6 =3,34 1028 m-3. La distance moyenne est obtenue en prenant l'inverse de la racine cubique du nombre précédent : d = n-1/3=3,1 10-10 m ~0,3 nm. En déduire le nombre de molécules d'eau qui traverse un nanotube de carbone par nanoseconde. D/d3 = D n = 1,3 10-23 3,34 1028  =4,3 105 s-1 = 4,3 10-4 ns-1.  Dans leurs expériences, Holt et al. observent un flux de l'ordre de 0,5 molécule par nanotube et par nanoseconde. Comparer ce résultat à celui prédit par le modèle de Poiseuille. Commenter. Résultat 1000 fois plus petit que la valeur expérimentale. Le modèle de Poiseuille ne convient pas pour ce type d'écoulement.

menu