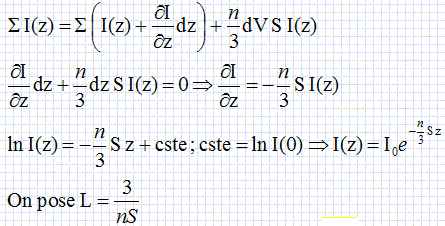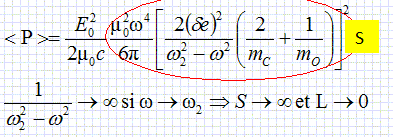Un gaz à effet de serre, le dioxyde de carbone : concours agrégation interne  2010 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

L'atmosphère terrestre. On considèrera que le Soleil se comporte comme un corps noir à la température TS et que la terre se comporte comme un corps noir à la température T0. Expliquer à quoi correspondent F, T et s dans la loi de Stefan : F = s T4 ? Le Soleil suit de manière satisfaisante un modèle très simple, qui suppose que chaque élément de sa surface émette une puissance surfacique ( W m-2)  F = s T4, où s = 5,67 10-8 W m-2 K-4 est appelée constante de Stefan. TS est la température de la surface du Soleil. Quelle est l'expression de la puissance totale rayonnée par le Soleil ? Surface d'une sphère de rayon RS : 4 p RS2. Puissance totale rayonnée : PS = 4 p RS2 s TS4 . Quelle est l'expression de la puissance reçue par la terre ? On considère qu'il n'y a pas de pertes : cette puissance se conserve. On note d la distance terre-Soleil. A la distance d du soleil, le flux surfacique F reçu orthogonalement est : F 4 p d2 = s TS4 4 p R2S ; F= s TS4  (RS / d)2. Si l'on considère d très supérieure au rayon terrestre RT, on peut considérer que la terre intercepte le rayonnement solaire par un disque de rayon RT. Puissance reçue par la terre : P =F  p RT2 = s TS4  (RS / d)2 p RT2. Déterminer la température de surface du Soleil sachant que le maximum du spectre qu'il émet se situe à lm =520 nm. La loi de Wien qui relie lm (longueur d'onde pour laquelle la densité spectrale d'un rayonnement à l'équilibre thermique est maximum ) à la température T à l'équilibre est : lm T = 2898 µm K.émise par un corps chaud. TS = 2898 / 0,52 =5573 ~ 5,6 103 K. En réalité la terre réfléchit une partie de l'énergie qu'elle reçoit et absorbe le reste. La fraction réfléchie s'appelle l'albédo qu'on note A et dont on donne la valeur numérique A = 0,34. Déterminer la température de la terre T0 en régime permanent. Flux surfacique reçu à la surface de la Terre : F= s TS4  (RS / d)2  ;  Flux surfacique réémis : A s TS4  (RS / d)2 .  A s TS4  (RS / d)2 = s T04  ;  T0 =TS  (RS / d)½ A0,25 ;  T0 = 5573 ( 7 108/1,5 1011 )½ 0,340,25 =290,7 ~291 K. Avec le modèle qui va suivre, on souhaite interpréter le fait que le sol terrestre est en réalité à une température T '0 supérieure à T0. C'est l'effet de serre. 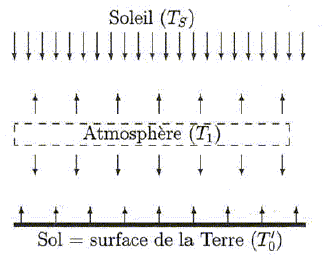 On considère donc le sol à la température T '0 et l'atmosphère à la température T1. L'atmosphère est assimilé à une couche sphérique dont le centre est celui de la terre et d'épaisseur e, avec e<<RT. Le sol et l'atmosphère sont supposés rayonner comme des coprs noirs de température respectives T '0 et T1. Si on assimile une sphère de rayon RT+e à une sphère de rayon RT ( e<<RT ), quelle est l'erreur relative commise sur le calcul de la surface ? A.N : e = 10 km. [4 p(RT+e)2 -  4 pRT2 ] / (4 pRT2) = (2RT+e) e / RT2 ~2e / RT ~ 20 / 6400 ~3,1 10-3.    L'atmosphère absorbe la fraction a du rayonnement solaire et absorbe complètement le rayonnement terrestre. Par ailleurs, elle émet vers la terre et vers l'espace. La terre absorbe le reste du rayonnement solaire et absorbe le rayonnement de l'atmosphère vers la terre. Les échanges sont symbolysés dans le schéma ci-dessous, où les flèches représentent les rayonnements. L'ensemble terre-atmosphère a le même albédo que la terre seule. Effectuer un bilan thermique pour le sol et un bilan thermique pour l'atmosphère. Sol : (A-a ) flux surfacique solaire - flux surfacique du rayonnement terrestre + flux surfacique reçu de l'atmosphère. (A-a) s TS4  (RS / d)2-s T '04+ s T'14 = 0 ; avec  TS4  (RS / d)2 = T04 /A. (A-a) /A T04 - T '04+  T14=0 (1) Atmosphère :  a flux surfacique solaire + flux surfacique du rayonnement terrestre - flux surfacique émis vers la terre et l'espace.  a  sTS4  (RS / d)2+ s T '04-2 s T'14 = 0 ; a /A T04  +  T '04- 2T14 =0 (2). Calculer T1 et T '0 si a = 0,33. Flux surfacique émis vers l'espace = s T'14 =A sTS4  (RS / d)2 = s T04  ;  T0 =T1. (2) donne : T '0=  T0 [2 -a /A ]0,25 =1,00727 T0 = 292,8 ~293 K. Un gaz à effet de serre, le dioxyde de carbone. Quel est le nom du protocole international qui réglement les émissions de gaz à effet de serre ? Quelle est l'année de sa signature ? Protocole de Kyoto signé en 1997. Mouvement d'élongation d'une molécule de CO2. Soit une molécule de dioxyde de carbone constituant un système isolé. Chaque liaison carbone-oxygène est indépendante de l'autre. Les atomes sont assimilés à des points matériels de masse mO =2,7 10-26 kg pour l'oxygène et mC = 2,0 10-26 kg pour le carbone. L'atome de carbone interagit avec ses deux voisins, les deux atomes d'oxygène, lesquels n'interagissent pas entre eux. A l'équilibre les deux liaisons carbone-oxygène sont identiques et ont donc même longueur. Les trois atomes restent toujours alignés. Au voisinage de l'équilibre, on  modèlise les deux liaisons carbone-oxygène par deux ressorts identiques de constante de raideur k = 1,4 103 Nm-1 et de longueur à vide l0 =0,17 nm. 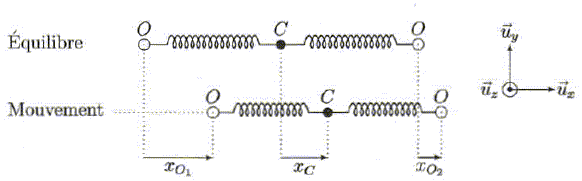On  repère par xO1, xC et xO2 les déplacements des atomes par rapport à la position d'équilibre de la molécule. On étudie la molécule de CO2 dans son référentiel barycentrique R*. Justifier que dans cet exemple, R* est galiléen .. La molécule constitue un système isolé ; la somme vectorielle des forces extérieures appliquées à la molécule est donc nulle. En conséquence, le vecteur accélération du centre d'inertie est nul et le vecteur vitesse du centre d'inertie G est un vecteur constant. R* étant en translation par rapport au référentiel d'étude, supposé galiléen, R* est galiléen. Justifier la relation  : mO (xO1 + xO2) + mCxC=0. 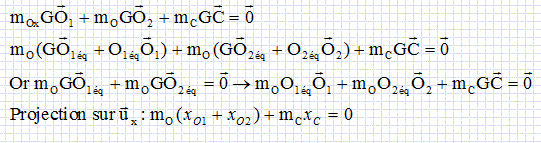Etablir le système d'équations différentielles vérifiées par x01 et xO2 par application du principe fondamental de la dynamique. mO x"O1 = -k( xO1-xC) avec xC = - mO( xO1+ xO2) / mC. x"O1 + k ( xO1 /mO+( xO1+ xO2) / mC))=0. (3) mO x"O2 = -k( xO2-xC)  ; x"O2 + k ( xO2 /mO+( xO1+ xO2) / mC))=0. (4) Les solutions sont de la forme x01(t) =A01 exp(iwt), x02(t) =A02 exp(iwt) et xC(t) =AC exp(iwt), en notation complexe. Déterminer les pulsations w1 et w2 conduisant à A01, A02 et AC non nuls. ( On prendra w1 <w2 ). x"O1 = A01 (-w2) exp(iwt) ; (3) s'écrit : [ A01 (-w2)  + k ( A01 /mO+( A01+ A02) / mC))]exp(iwt)=0. x"O2 = A02 (-w2) exp(iwt) ; (4) s'écrit : [ A02 (-w2)  + k ( A02 /mO+( A01+ A02) / mC))]exp(iwt)=0. A01( -w2 + k /mO + k /  mC) + k A02 / mC=0 et  k A01 / mC + A02( -w2 + k /mO + k /  mC)  =0. Le déterminant doit être égal à zéro  :  ( -w2 + k /mO + k /  mC)2 =( k /  mC)2. -w2 + k /mO + k /  mC= k /  mC ; w2 = k /mO ;  w1 = (k /mO)½. et -w2 + k /mO + k /  mC = - k /  mC ; w2 = ( 2k /  mC+ k /mO)½. Comment s'appellent ces pulsations ? Les calculer. w1 et w2 sont les pulsations propres de la molécule de CO2. w1 = (1400 /2,7 10-26)½= 2,3 1014 rad/s ; w2 = ( 2800 / 2,0 10-26+ 1400 /2,7 10-26)½ = 4,4 1014 rad/s. Décrire brièvement le mouvement de la molécule pour w1 et w2. Pour w1 : A01(  k /mO ) + k A02 / mC=0  ; A01 = - A02 ; mO x"O2 = -k( xO2-xC) ; mO A01 (-w2) = -k(  A02-AC) ; k A01 = -kA02 + k AC d'où AC=0. Les atomes d'oxygène vibrent symétriquement de part et d'autre du carbone fixe. Pour w2 :   A01(  -k /mC ) + k A02 / mC=0  ; A01 = + A02 ; mO x"O2 = -k( xO2-xC) ; mO A01 (-w2) = -k(  A02-AC) ; -mO  A01 (k /mO + 2k /  mC )= -kA02 + k AC  d'où AC=  -2A01 mO/  mC . Les atomes d'oxygène vibrent dans le même sens de part et d'autre du carbone mobile. Propagation d'une onde électromagnétique dans l'atmosphère contenant du CO2. Les liaisons carbone-oxygène sont des dipôles. Chaque oxygène porte la charge -de et le carbone porte la charge + 2de. ( 0 < d < 1 ). La molécule de CO2 est supposée toujours rester alignée selon  ux ; elle est dans le plan z=0. Une onde électromagnétique de pulsation w, polarisée suivant  ux et va rencontrer une molécule de CO2. On appelle cette onde l'onde incidente. Son champ électrique est de la forme : 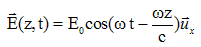où c est la célérité de la lumière dans le vide. On néglige l'action du champ magnétique. Justifier que R* est encore galiléen. La molécule de CO2 est globalement neutre : la force électrique totale est donc nulle. La somme vectorielle des forces extérieures appliquées à la molécule est toujours nulle. En conséquence, le vecteur accélération du centre d'inertie est nul et le vecteur vitesse du centre d'inertie G est un vecteur constant. R* étant en translation par rapport au référentiel d'étude, supposé galiléen, R* est galiléen. Etablir le système d'équations différentielles vérifiées pr xO1 et xO2, par application du principe fondamental de la dynamique. Aux équations précédentes on ajoute le terme -de E0cos (wt). x"O1 + k ( xO1 /mO+( xO1+ xO2) / mC))= -de E0cos (wt) (5)  x"O2 + k ( xO2 /mO+( xO1+ xO2) / mC)) = - de E0cos (wt). (6) En régime sinusoïdal forcé, les solutions, en notation complexe, sont de la forme : x01(t) =A01 exp(iwt), x02(t) =A02 exp(iwt). Déterminer A01 et A02 en fonction de d, e, E0, w, w2, mO. (5) s'écrit : A01( -w2 + k /mO + k /  mC) + k A02 / mC = -de E0 / mO ; A01( -w2 + w22 - k /  mC) + k A02 / mC = -de E0 / mO ;  et (6) s'écrit :  k A01 / mC + A02( -w2 + k /mO + k /  mC)  = -de E0 / mO ; k A01 / mC + A02( -w2 + w22 - k /  mC)  = -de E0 / mO. (5) +(6) : ( -w2 + w22 ) (A01+ A02)  = -2de E0 / mO ; (5) s'écrit : A01( -w2 + k /mC + w12) +  k A02 / mC = -de E0 / mO ;   et (6) s'écrit :  k A01 / mC + A02( -w2 + k /mC +w12)  = -de E0 / mO. (5) -(6) :  ( -w2 + w12 )(A01- A02)= 0. Pour w dirfférent de w1 et différent de w2 : A01= A02 ; A01 = de E0 / (mO (  w22 -w2 )). Exprimer le moment dipolaire de cette molécule en fonction de  d, e, E0, w, w2, mO, mC et t. On notera A le barycentre des charges négatives, B le barycentre des charges positives et Céq la position d'équilibre du carbone. 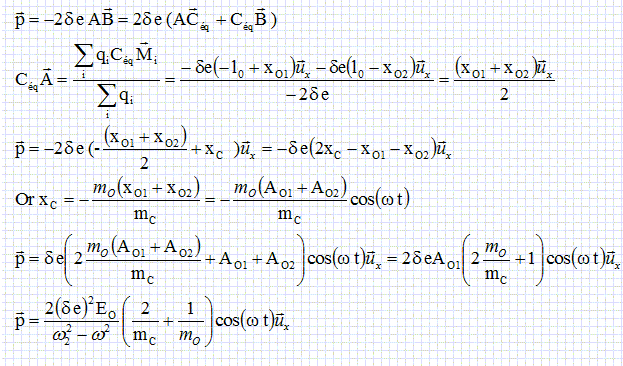Une molécule de CO2 est donc modélisée par un dipôle rayonnant. 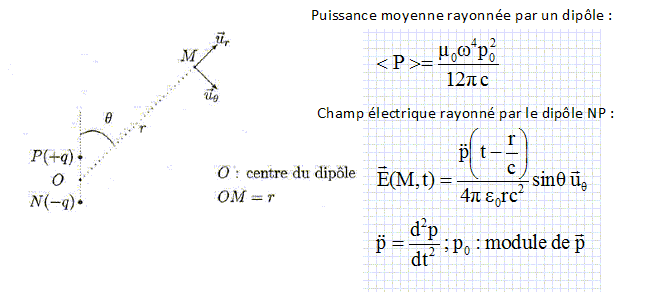D'où vient la puissance quatrième w4 dans l'expression de <P> ? Dans le calcul de la puissance surfacique, le vecteur de Poynting intervient : 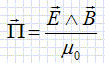Dans l'expression de E, on trouve la dérivée seconde p'' dans laquelle intervient le facteur w2. De plus B = E / c : dans l'expression de B, on trouve également w2. Exprimer la puissance moyenne I0 en z=0 transportée par l'onde incidente en fonction de µ0, c et E. Expression de la valeur moyenne de la norme du vecteur de Poynting : I0 = <EB / µ0> avec de plus B = E / c, d'où : I0 =<E2 / (µ0c)> Le champ électrique de l'onde incidente est de la forme : 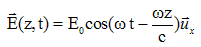. La valeur moyenne du carré d'un cosinus est égale à ½ ; la valeur moyenne de E2 est en conséquence ½E02. par suite : I0 =<E2 / (µ0c)> = E02/ (2µ0c). En déduire que <P> = SI0 et exprimer S en fonction des données. <P> = puissance surfacique fois une surface notée S = S I0. 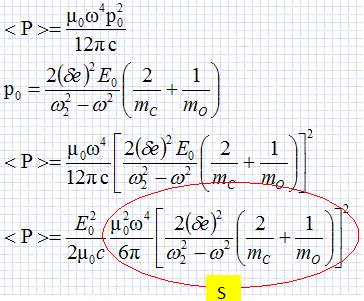L'atmosphère contient n molécules de CO2 par unité de volume. On considérera q'un tiers d'entre elles sont alignées dans chacune des directions de l'espace. Les molécules de CO2 rayonnent de l'énergie qu'elles prennent à l'onde incidente et l'intensité de l'onde incidente diminue donc avec z. Effectuer un bilan d'énergie sur un volume élémentaire de hauteur dz et en déduire que I(z) est de la forme I(z) = I0 exp(-z/L) avec I(0) = I0. Exprimer L en fonction de S et n. Ecrire que la puissance incidente  I(z) S est égale à la somme de la puissance sortante I(z+dz) S et de la puisance diffusée par le dioxyde de carbone. L : distance caractéristique de pénétration de l'onde. Expliquer pourquoi l'onde est fortement absorbée pour w tendant vers w2 et non absorbée pour w tendant vers w1. Pour w = w1 : les atomes d'oxygène vibrent symétriquement de part et d'autre du carbone fixe sous l'action du champ électrique Calculer la longueur d'onde dans le vide l2 correspondant à la pulsation w2. A quel domaine du spectre électromagnétique appartient-elle ? Conclure. w2 =2 p f = 2 p c / l2 ;  l2 =2 p c / w2 = 6,28 *3,0 108 / 4,4 1014 = 4,3 10-6 m ( IR). Le dioxyde de carbone de l'atmosphère absorbe les rayons IR émis par la terre.  l'atmosphère renvoie une partie de cette énergie absorbée vers le sol : ce phénomène contribue à l'effet de serre. Conséquence de l'augmentation de CO2 dans l'atmosphère. On suppose que le quantité de CO2 augmente et on modélise cette augmentation par la superposition de N couches de CO2 gazeux entourant la terre. Chaque couche contient  la même concentration fixée C0 en CO2 gazeux. Le sol terrestre se comporte comme un corps noir de température T0 et émet un flux surfacique Ft. On ne tient pas compte ici de l'albédo de la terre. FS est le flux solaire reçu par la terre, par unité de surface de la terre. FP est le flux surfacique émis vers le haut et vers le bas par la couche p, de température TP. Le rayonnement émis par une couche est complétement absorbé par les autres couches. Les couches sont transparentes au rayonnement solaire, qui arrive sous incidence normale sur chaque couche. A partir d'un ordre de grandeur usuel pout T0, déterminer l'ordre de grandeur de la longueur d'onde d'émission maximum du sol terrestre. lm T0 = 2898 µm K avec T0~293 K. lm ~2898 / 293 ~10 µm. ( IR ). Le dioxyde de carbone de la couche 1 absorbe les rayons IR émis par la terre. Effectuer un bilan radiatif pour : Le sol : Ft = FS+F1. Sol et couche 1 : F1 = FS+F2. Sol et couches 1 à p : Fp = FS+Fp+1. Sol et couches 1 à p : FN = FS. En déduire d'une part  Fp en fonction de FS, N et p et d'autre part Ft en fonction de FS et N. Fp+1 = FS+Fp+2 ; Fp =2 FS+Fp+2 = 3 FS+Fp+3  = ... =(N-p) FS +FN ; Fp= (N+1-p) FS. Ft = FS+F1= FS+N FS = (N+1) FS. Déduire de la loi de Stefan l'expression de T0 en fonction de FS, N et s, la constante de Stefan. Ft = sT04  = (N+1) FS ; T0  = [(N+1) FS /s]0,25. N et en conséquence T0 augmentent avec la quantité de CO2.

menu