Moteur
à courant continu.
Une machine d'extraction est entraînée par un moteur à courant continu
à excitation indépendante. L'inducteur est alimentée par une tension Ue
= 600 V et il est parcouru par un courant
d'excitation d'intensité Ie =30 A ; il se
comporte comme un conducteur ohmique de résisatnce r.
L'induit de résistance R = 12 10-3 ohm est
alimenté par une source fournissant une tension U réglable entre 0 V et
sa valeur nominale UN = 600 V.
La valeur nominale de l'intensité du courant dans l'induit est IN =1,5 103
A. La fréquence de rotation nominale est nN = 30
tr/min.
Phase
de démarrage.
On note W
la vitesse angulaire du rotor ; la force électromotrice du
moteur a pour expression E = K W.
Donner
la valeur de E à l'arrêt.
A l'arrêt, le rotor ne tourne pas : W =0 et en
conséquence E = 0.
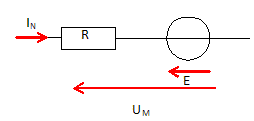
Représenter
le modèle équivalent de l'induit du moteur en indiquant sur le schéma
les flèches associées à U et I ( I intensité du courant
dans l'induit ).
|
Ecrire la
relation entre U, E et I, puis en déduire la tension Ud
à appliquer au démarrage pour un courant d'intensité Id
= 1,2 IN.
U = E + R I ;
Au démarrage E 0, d'où : Ud = RId
=12
10-3 *1,2*1,5 103
= 21,6 ~22 V.
|
Fonctionnement
nominal au cours d'une remontée en charge.
Exprimer
littérallement puis calculer :
La
puissance Pinduit reçue par l'induit du moteur,
alimenté par une source à sa valeur maximale.
Pinduit
= IN UN =1,5 103 *600 = 9,0 105
W =9,0
102 kW.
La
puissance Pinducteur reçue par l'inducteur du
moteur.
Pinducteur
= Ue
Ie
= 600*30 = 1,8 104 W =18 kW.
La
puissance totale Ptot reçue par le moteur.
Ptot
= Pinducteur
+ Pinduit
=18 +9,0 102 = 918 ~9,2 102 kW.
La
puissance totale PJ perdue par effet Joule.
PJ
= Ue
Ie +RIN2
=600*30
+12
10-3(1,5 103)2
=4,5 104 W = 45 kW.
Sachant
que la puissance dissipée par les autres types de pertes (
autres que les pertes par effet Joule ) apour valeur
PC = 27 kW ,
vérifier
que la puissance utile Put du moteur
vaut environ 850 kW.
Put
= Ptot
-PJ
-PC
=918-45-27 =846 kW ~8,5 102 kW.
En déduire
le moment Tu du couple
utile du moteur.
Vitesse
angulaire W
= 2 p f
avec f = 30/60 = 0,50 tr / s ( Hz ) ; W =3,14 rad/s.
Tu
= Put / W
= 846 103 / 3,14 =2,7 105 N m.
Calculer
le rendement h du moteur.
h = Put
/Ptot
=846 / 918 =0,92
( 92 %).
Fonctionnement d'un
moteur de type turbine à gaz à combustion externe
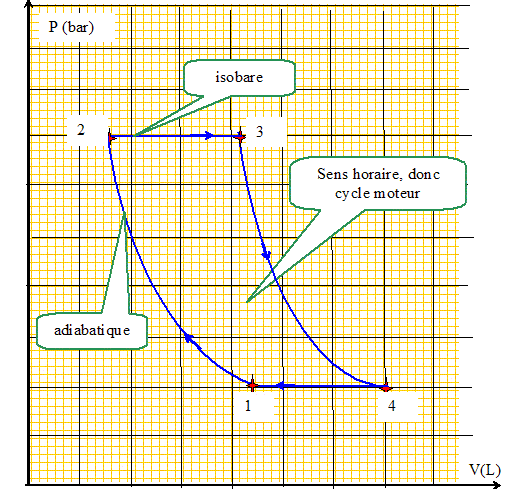
Dans
une machine thermique, un gaz, assimilé à un gaz parfait, décrit le
cycle de tansformations suivantes :
initialement à l'état 1, à la pression p1 et à
la température T1, il traverse un compresseur
dans lequel il subit une évolution adiabatique réversible jusqu'à
l'état 2 où sa pression est p2 et sa température
T2.
Il
se trouve alors au contact avec une source chaude et se réchauffe, de
façon isobare, jusqu'à la température T3 où il
est à l'état 3.
Il pénètre ensuite dans la turbine où il se détend de manière
adiabatique réverible, jusqu' à la pression p4.
Il est alors à l'état 4 ; sa température est T4.
Il achève de se refroidir, d'une façon isobare, au contact d'une source
froide et se retrouve à l'état p1.
Quelle
est la relation entre p2 et p3
?
2 --> 3 : réchauffement isobare : p2 = p3.
Tracer
l'allure du cycle décrit par le gaz dans un diagramme de Clapeyron p=
f(V).
Lors d'une évolution diabatique
réversible, le gaz parfait obéit à la loi PVg =
cste avec g
= Cp/Cv.
Cp :
capacité thermique molaire à presion constante ; Cv
: capacité
thermique molaire à volume constante.
Démontrer
que cette loi peut s'écrire P1-g Tg =
constante.
PV = nRT ; V = nRT / P ; Vg =(nR)g
Tg
P-g
;
PVg
=P(nR)g
Tg
P-g
= (nR)g
Tg
P1-g
= cste avec (nR)g
constant ; par suite Tg
P1-g
= autre constante.
En déduire
l'expression :
de la température T2 en
fonction de p1, p2, T1
et g.
T1g
P11-g
=T2g
P21-g
; T1
P1(1-g
)/g
=T2
P2(1-g)/g ; T2
=T1
(P1/ P2)(1-g
)/g
.
de la température T4 en fonction de p1,
p2, T3 et g.
T4g
P41-g
=T3g
P31-g
; T4
P4(1-g
)/g
=T3
P3(1-g)/g ; T4
=T3
(P3/ P4)(1-g
)/g
.
Or p2
= p3 et p1
= p4. ( évolutions isobares ).
T4
=T3
(P2/ P1)(1-g
)/g
.
Pour n = 1 mole de gaz parfait, exprimer
en fonction de Cp et des
températures adéquates :
QC, l'énergie échangée sous
forme de chaleur avec la source chaude.
QC = CP(T3
-T2).
QF, l'énergie échangée sous
forme de chaleur avec la source froide.
QF = CP(T1
-T4).
En
utilisant le premier principe, donner l'expression Wcycle de
l'énergie échangée sous forme de travail mécanique par une mole de gaz
parfait avec l'extérieur au cours du cycle, en fonction de CP et des températures.
Wcycle +
QC + QF
= 0 ; Wcycle
= -QC
- QF = CP(T4
+T2 -T3
-T1).
Le rapport t
=P2/P1 est imposé par les
limites de la résistance mécanique du compresseur.
Le rendement théorique h
de cette machine s'écrit : h = 1-t(1-g
)/g.
Calculer
le rendement pour les trois gaz du tableau suivant en prenant t =4,0.
Avec lequel obtient-on le meilleur rendement ?
Gaz
|
argon
|
air |
dioxyde
de carbone |
valeur
de g
|
1,67
|
1,40
|
1,31 |
rendement
|
0,43
|
0,33
|
0,28 |
Le meilleur rendement est obtenu avec l'argon.
Calculer
les températures T2 et T4
pour le gaz qui donne le meilleur rendement.
p1
= 1,0 105 Pa ; T1
= 300 K ; T3
= 900 K.
T2
=T1
(P1/ P2)(1-g
)/g
= 300 *0,25-0,4012 =523 K.
T4
=T3
(P2/ P1)(1-g
)/g
=900*4-0,4012 =516 K.
|
|
Solution
d'hydroxyde de sodium.
Une solution d'hydroxyde de sodium, S1, est fabriquée en dissolvant m = 2,0 g d'hydroxyde de sodium solide NaOH, dans V = 5,0 L d'eau pure.
Calculer la quantité de matière, n, d'hydroxyde de sodium.
n = m/MNaOH = 2,0 / 40 = 0,050 mol.
Calculer la concentration molaire C de cette solution.
C = n / V = 0,050 / 5,0 = 0,010 mol/L.
Calculer [HO-] et [H3O+].
[HO-] = C = 0,010 mol/L ; [H3O+] = 10-14 / [HO-] = 1,0 10-12 mol/L.
Vérifier que le pH de cette solution est 12.
pH = -log [H3O+] =-log(1,0 10-12) = 12.
Une solution S2 se colore en rouge avec l'hélianthine, en jaune avec le bleu de bromothymol et reste incolore avec la phénolphtaléine. En utilisant le tableau ci-dessous, déduire un encadrement de la valeur du pH. Justifier. | nom de l'indicateur | couleur de l'indicateur | | hélianthine | rouge : pH <3,2
orange : 3,2 < pH < 4,4
jaune : pH >4,4. | | bleu de bromothymol | jaune : pH <6
vert : 6 < pH < 8
bleu : pH >8. | | phénolphtaléine | incolore : pH <8,2
rose : 8,2 < pH < 10
violacé : pH >10. |
L'hélianthine est rouge : le pH est inférieur à 3,2. Le bleu de bromothymol est jaune : pH < 6 ; la phénolphtaléine est incolore : pH < 8,2.
La mesure du pH donne 2,9. Calculer [HO-] et [H3O+].
[H3O+] = 10-pH =10-2,9 =1,26 10-3 ~1,3 10-3 mol/L.
[HO-] =10-14 / [H3O+]= 10-14 /1,26 10-3 ~7,9 10-12 mol/L.
Cette solution est-elle acide, neutre ou basique ?
A 25°C, si le pH est inférieur à 7, la solution est acide.
|

