|
|
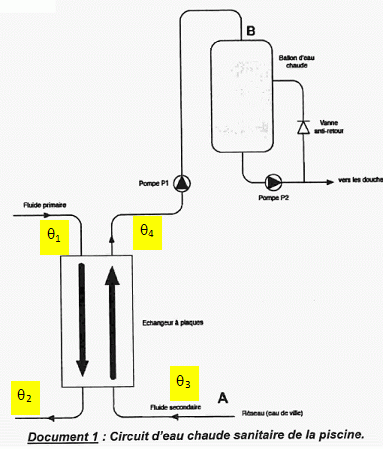
Etude de
l'échangeur.
L'eau chaude primaire arrive à une température q1 = 75°C avec un débit
Qp=20 m3 h-1 et ressort à la
température q2.
Le circuit d'eau secondaire provient du réseau d'eau de ville. L'eau
entre dans l'échangeur à la température q3
= 10°C et ressort à la température q4
= 55°C avec un débit Qs=100
L min-1. L'échangeur est considéré comme parfaitement
adiabatique.
Montrer que la
puissance Pf reçue par l'eau
froide est 313,5 kW.
Pf = Qs reau
C(q4
-q3).
Qs =0,100 / 60 = 1,6667 10-3
m3 s-1 ; reau= 1000 kg m-3 ; C =
4180 J kg-1 K-1.
Pf =1,6667 10-3
*1000*4180*(55-10) =3,135 105 W = 313,5 kW.
En
déduire la puissance PC fournie par l'eau chaude.
L'échangeur étant adiabatique, la puissance reçue par l'eau froide est
égale à la puissance fournie par l'eau chaude.
Pc =313,5
kW.
Déterminer
q2.
Pc = Qp reau C(q1 -q2) ; q2 =q1
-Pc
/( Qp reau
C)
Qp=20
m3 h-1 = 20 / 3600 = 5, 555 10-3
m3 s-1 ;
q2 =75
-3,135 105 /( 5, 555 10-3*1000*4180) = 61,5°C.
On rappelle l'expression de la différence de température moyenne
logarithmique :
DqmL
=( Dqe- Dqs) / ln ( Dqe/Dqs).
Dqe différence de température d'entrée et Dqs différence de température de sortie en choisissant
arbitrairement l'entrée et la sorite de l'échangeur à contre courant.
Montrer
que DqmL =33,3°C.
Dqe = 61,5-10 = 51,5°C ; Dqs = 75-55 = 20°C ;
DqmL =(51,5-20) / ln
(51,5 /20 ) =33,3°C.
En
déduire la surface S de l'échangeur. K = 1880 Wm-2K-1.
Pc = KS DqmL ; S = Pc
/( K DqmL )= 3,135 105 /
(1880*33,3) =5,0 m2.
|
.
Etude du
circuit secondaire.
Le branchement au réseau de ville se fait
au point A et lorsque le volume d'eau du réservoir de stockage ( ballon
d'eau chaude ) atteint une valeur minimum, la pompe P1 se
met en marche jusqu'à un volume maximum où elle s'arrête. Quand la
pompe est en marche, Qs = 100 L min-1.
La canalisation du circuit secondaire a un diamètre d = 5 cm.
Calculer
la vitesse de l'eau dans cette canalisation.
v = Qs / (0,25 pd2)
=1,6667 10-3 /'0,25*3,14*0,052) =0,85 m/s.
Par la suite on prendra
v = 0,8 m/s.
Calculer
le nombre de Reynolds associé à cet écoulement.
Re = r v d / h avec h = 1,0 10-3 Pa s.
Re = 1000*0,8*0,05 / 1,0 10-3 =4,0
104.
En
déduire la nature de l'écoulement.
L'écoulement est turbulent.
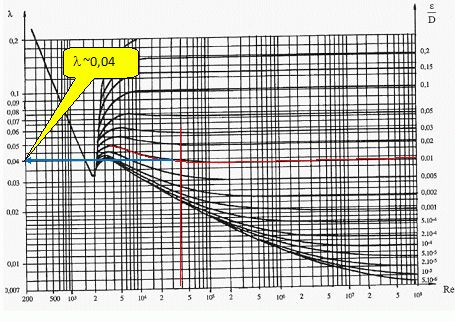
La rugosité de la canalisation est e
= 0,5 mm.
Déterminer
graphiquement le coefficient de perte de charge l.
e / d = 0,5 / 50 = 0,01.
Dimensionnement
de la pompe.
Longueur de la tuyauterie AB : L = 50 m ; l'échangeur crée une perte de
charge globale égale à une longueur équivalente L1 =
100 m ; chaque coude crée une perte de charge égale à une
longueur équivalente L2 = 2 m.
La dénivellation entre A et B est h = 20 m. PB = 1 bar ; PA
= 2,5 bar ; l = 0,04 ; g =
10 SI.
Calculer
la perte de charge totale DHAB du circuit entre
les points A et B.
DHAB =l(L+SLeq)v2 /
(2gd).
SLeq= L1 +5L2 =100 +5*2 = 110 m.
DHAB =0,04(50+110)*0,82 /
(2*10*0,05) = 4,1
m.
En appliquant le
théorème de Bernoulli entre A et B, calculer la hauteur manométrique Hpompe de la pompe.
v2B
/ 2g + zB +PB /(rg)
-(v2A /
2g + zA +PA /(rg)) = -DHAB + Hpompe.
vB = vA,
conservation du débit volumique ( tuyaux de même diamètre ).
zB
+PB /(rg) -( zA +PA /(rg)) = -DHAB + Hpompe ;
Hpompe = zB -zA + DHAB +PB /(rg) -PA /(rg)
Hpompe =20 +4,1 - 1,5 105/(1000*10) = 9,1 m.
On prendra par la suire Hpompe = 40 m.
En
déduire la puissance mécanique reçue par le fluide.
Putile = r g Qs
Hpompe =1000*10*1,6667 10-3 *40 =670 W.
La pompe a un rendement de 70 %.
Quelle
sera la puissance absorbée par le moteur de la pompe ?
670 / 0,7 = 950 W.
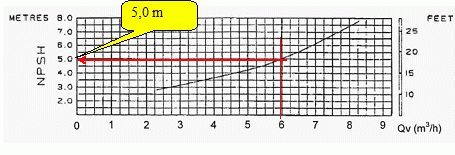
Déterminer
le NPSH requis.
Qs = 6 m3 h-1 ;
Quel
doit être la condition sur le NPSH disponible pour éviter le phénomène
de cavitation ?
Le NPSH disponible du circuit doit être supérieur au NPSH requis de la
pompe.
|
|


