Viscosité du diazote liquide
Un rhéomètre rotatif cylindrique
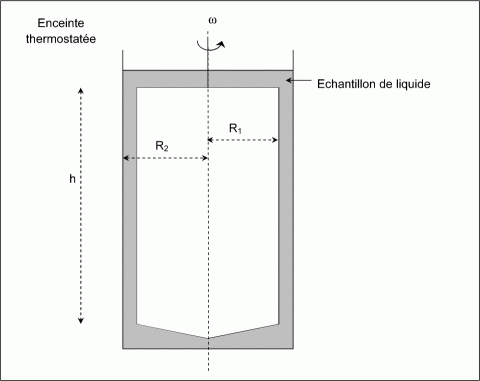
permet de mesurer la viscosité dynamique hN2 du diazote liquide, supposé newtonien. Il est
constitué d’un cylindre intérieur, de rayon R1, de hauteur h,
immergé dans l’échantillon liquide à l’intérieur d’un cylindre extérieur de
rayon R2. On mesure pour cela un couple M, en fonction d’une vitesse
de rotation du cylindre extérieur imposée w.
Généralités.
On étudie la variation d’une contrainte de
cisaillement t en fonction d’une vitesse
de déformation D. La
loi reliant t et D est écrite sous la forme t = k Dn.
Que peut-on dire de n pour
un fluide rhéofluidifiant ?
n < 1: fluide rhéofluidifiant.
Que peut-on dire de n pour
un fluide newtonien ?
n = 1 : fluide newtonien.
Dans le cas d’un fluide newtonien, on peut
montrer la relation suivante entre les paramètres du rhéomètre, et les
grandeurs mesurées : M = 2 p h w h R13 / (R2-R1). (1)
où w est
exprimée en rad.s-1, M en N.m, et les autres grandeurs également dans
les unités S.I.
Vérifier
l’homogénéité de l’expression (1).
[R13 / (R2-R1)]= L2 ( m2) ; [h] = L ( mètre) ; [w ]= T-1 ; h : viscosité ( Pa s) soit une pression fois un temps ou encore une force / surface fois un temps. [h] = force T L-2.
Par suite : [h w h R13 / (R2-R1)] = L T-1 force T L-2 L2 = L force ( newton mètre ).
|
Mettre la relation (1) sous la forme M = Kh ; donner l’expression de K et calculer sa valeur numérique.
M = 2 p h w h R13 / (R2-R1) ; M = K h ; K = 2 p w h R13 / (R2-R1).
R1
= 5,50 mm ; R2 = 6,00 mm ; h = 8,00 mm ; w =
1,0 rad.s-1.
K = 2*3,14 *1,0 *8,00 10-3*(5,50 10-3)3 / ((6,00-5,50)10-3)=1,6726 10-5 ~ 1,67 10-5 m3 s-1.
|
On
utilise comme fluide étalon du dioxygène liquide, de viscosité connue hO2 . Le couple mesuré
est alors MO2. À la même vitesse de rotation, on mesure
pour le diazote liquide MN2.
En appliquant l’expression (1) à chaque
espèce, exprimer la viscosité dynamique hN2 en fonction de MO2, hO2, et MN2 Faire l’application numérique. Comment varie
la viscosité dynamique avec la température ?
Données : Fluides : hO2 = 1,90 × 10-4 Pa.s ; MO2 = 1,66 × 10-6 mN.m MN2= 1,40 × 10-6 mN.m.
MO2 =K hO2 ; MN2 =K hN2 ; hN2 = hO2 MN2 / MO2 =1,90 × 10-4 *1,40 / 1,66 =1,60 10-4 Pa s.
La viscosité dynamique augmente avec la température.
Equilibre liquide /vapeur du diazote
On étudie le diazote au voisinage de la
courbe de saturation.
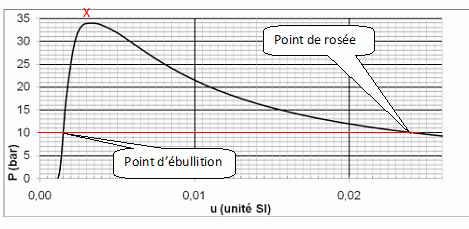
L’annexe 2 présente la courbe de
saturation dans les axes (P,u) , où u est la volume massique.
Définir
le point critique, noté X. Placer le point X sur la courbe de l’annexe 2.
Le point critique d’un corps pur est tel que la transition de phase entre l'état liquide et l'état gazeux est impossible.
Placer
sur cette même courbe, les points de rosée R et d’ébullition
E du diazote à la température T1 = 104 K.
A 104 K la pression de vapeur saturante du diazote liquide est P = 10 bars.
Le point de rosée ddu diazote est la température à laquelle la
pression partielle de vapeur du diazote est égale à sa pression de
vapeur saturante.
On
note uL et uV les volumes massiques, respectivement du
liquide et de la vapeur.
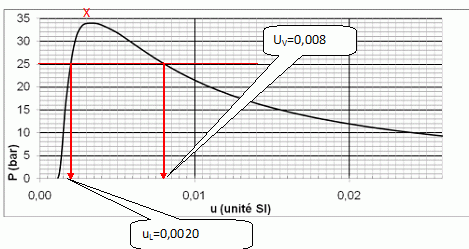
Déterminer uL et uV aux températures
T1 et T4 données dans
le tableau ci-dessous qu’on reproduira et complètera sur sa copie.
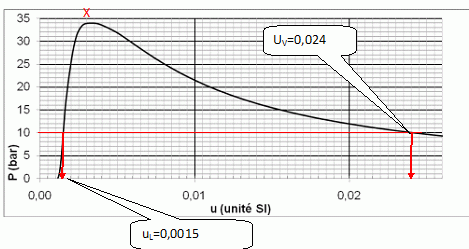
A 120 K la pression de vapeur saturante du diazote liquide est P = 25 bars.
T
|
T1=104 K
|
T4=120 K |
dPS/dT ( bar K-1)
|
0,6543
|
1,261
|
uL(SI)
|
0,0015
|
0,002
|
uV(SI)
|
0,024
|
0,008
|
LV(SI)
|
1,53
|
0,908
|
Que
peut-on dire de uL et uV au point X ?
Au point critique uV = uL.
|
|
La
chaleur latente massique Lv est donnée par la relation de Clapeyron :
LV = T ( uV-uL)dP/dT.
Préciser les unités des grandeurs
intervenant dans cette relation.
Lv : J kg-1 ; T : K ; P : Pa ; uV et uL : m3 kg-1.
Calculer
numériquement cette chaleur latente massique Lv aux températures T1,
et T4
T = 104 K : LV = 104(0,024-0,0015)*0,6543 = 1,53 J kg-1.
T = 120 K : LV = 120(0,008-0,002)*1,261 = 0,908 J kg-1.
Que
vaut la chaleur latente au point X ?
uV= uL conduit à LV=0 au point triple.
Décrire
l’évolution de Lv en fonction de la température T.
Lorsque la température augmente, LV diminue.
|



