Il s’agit ici d’étudier expérimentalement, au laboratoire, la
réponse du spectromètre de masse à temps
de vol, ou Time Of Flight (T.O.F.) à l’impact de glaces éventuelles de méthane
détectées autour de Saturne. Pour simuler la présence de ces glaces, du méthane
gazeux est condensé, pour former un dépôt solide, sur une cible à base de fer,
en contact avec du diazote liquide à 77 K.
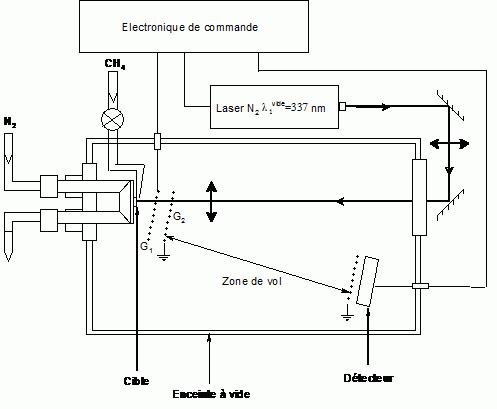
Le spectromètre TOF utilise un faisceau LASER, de longueur d’onde
dans le vide l1, qui
bombarde la cible et provoque la création d’ions positifs de vitesse considérée
comme nulle. Ces ions sont accélérés entre des grilles G1 et G2, puis
pénètrent dans une zone sans champ électrique (zone de vol) et atteignent enfin
un détecteur. L’objet de l’expérience est de caractériser la réponse des
différents ions issus de la glace de méthane.
On considère que les ions évoluent dans le vide et on négligera toute
influence de la pesanteur devant les autres forces mises en jeu.
Ionisation par LASER.
À
quel domaine du spectre électromagnétique les ondes émises par LASER de
longueur d’onde l1=337 nm
appartiennent-elles ?
337 nm est une longueur d'onde du proche ultraviolet.
Exprimer
littéralement en fonction des données l’énergie Ep d’un photon de
cette onde LASER. Faire l’application numérique.
Ep = h c / l1 =6,626 10-34 *2,998 108 / 337 10-9 =5,8946 10-19 ~5,89 10-19 J.
On
note t la durée d’une impulsion et N le nombre
de photons par seconde. Exprimer littéralement l’énergie d’une impulsion Ei.
Faire l’application numérique.
Ei = Ep N t =5,8946 10-19 *1,23 1023*4,00 10-9 =2,900 10-4 J.
Exprimer
littéralement en fonction des données la puissance P du LASER durant
l’impulsion et faire l’application numérique.
P = Ep N = 5,8946 10-19 *1,23 1023 =7,25 104 W.
|
Accélération des ions
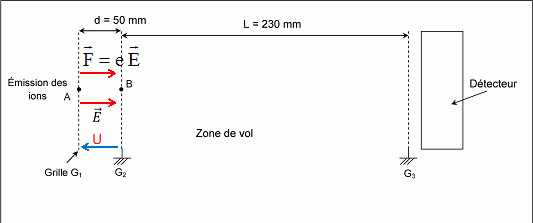
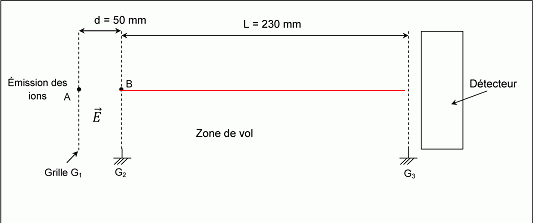
On note d la distance entre les grilles G1
et G2, et U la tension d’accélération appliquée entre ces grilles. On considère qu'en A les ions émis n’ont pas
de vitesse initiale.
Indiquer
en justifiant sur le schéma ,
l’orientation du champ électrique E en représentant le vecteur correspondant, de
façon que les ions soient accélérés vers la plaque G2 entre les
points A et B.
|
Exprimer
littéralement et calculer l’intensité E du champ électrique appliqué.
E = U / d = 700 / 50 10-3 =1,4 104 V m-1.
Redémontrer
l’expression de l’énergie cinétique EC(B) acquise par les ions à
leur passage en B à travers la grille G2.
Le poids des ions est négligeable devant la force électrique F = eE. Le
travail de cette force au cours du déplacement AB est W = e U.
Variation de l'énergie cinétique : Ec(B)-Ec(A) = W ; Ec(B -0 = e U ; Ec(B = eU.
En
déduire la vitesse vB atteinte en B au niveau de la plaque G2.
½mvB2 = eU ; vB = (2eU/m)½.
Faire l’application
numérique des vitesses vB(H+), vB(C+)
et vB(CH4+) des ions H+, C+ et CH4+.
(2eU)½= (2*1,602 10-19 *700)½ =1,4976 10-8 ; vB =1,4976 10-8 m-½.
vB(H+) =1,4976 10-8 (1,6726 10-27)-½= 3,6618 105 m/s.
vB(C+)=1,4976 10-8 (2,0089 10-26)-½= 1,0566 105 m/s.
vB(CH4+)=1,4976 10-8 (2,6783 10-26)-½= 9,151 104 m/s.
Exprimer les masses m(H+),
m(C+) et m(CH4+)
de ces ions en unité de masse atomique u.
m(H+) =1,6726 10-27 / 1,6605 10-27 =1,0073 u ;
m(C+) =2,0089 10-26 / 1,6605 10-27 =12,098 u ;
m(CH4+) =2,6783 10-26 / 1,6605 10-27 =16,130 u.
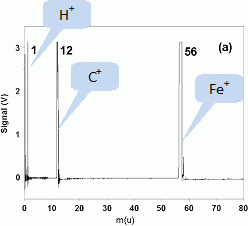
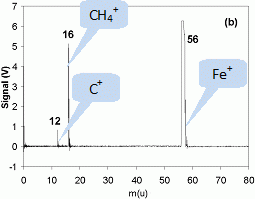
Les
schémas 2 a)
et 2b) correspondent à deux mesures successives. Identifier sur
ces schémas les ions présents pour chacune de ces mesures.
Vol des ions
Décrire en justifiant le mouvement des ions en l’absence de champ
électrique. Représenter sur le schéma la trajectoire des ions,
dans la zone de vol, depuis le point B jusqu’au point C où les ions coupent la
grille G3.
Le poids des ions est négligeable ; en l'absence de champ électrique,
la force électrique est nulle. Les ions n'étant soumis à aucune
force, le principe d'inertie indique que leur mouvement est rectiligne
uniforme.
Exprimer
littéralement le temps de vol t, mis par les ions pour parcourir la distance
entre la grille G2 et la grille G3 du détecteur, en
fonction de vB.
t = BC / vB = L / vB.
Montrer que le temps de
vol peut se mettre sous la forme t = L(m/(2eU)½.
vB = (2eU/m)½ d'où t = L(m/(2eU))½.
|
|
Quelle serait l’allure
de la courbe t2 en fonction de m. Justifier l’allure de la courbe obtenue.
t2 = L2 / (2eU) m.
L2 / (2eU) est une constante ; t2 est proportionnel à m. La courbe est une droite passant par l'origine.
Calculer
numériquement les temps de vol respectifs tH+, tC+ et tCH4+ des
ions H+, C+ et CH4+.
tH+ =L / vB(H+) = 0,230 / 3,6618 105 = 6,28 10-7 s.
tC+ =L / vB(C+) = 0,230 / 1,0566 105 = 2,18 10-6 s.
tCH4+ =L / vB(CH4+) = 0,230 / 9,151 104 = 2,51 10-6 s.
|