Fibre optique à saut d'indice.
Dans
ce type de fibre, l'indice de réfraction varie brusquement entre le
coeur et la gaine. Le schéma ci-dessous représente une coupe
longitudinale de la fibre.
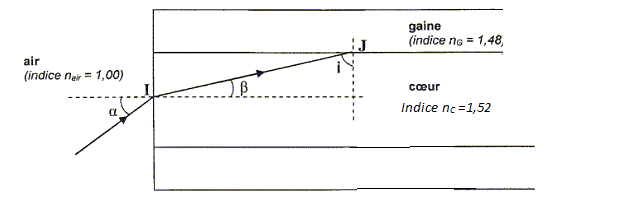
Un rayonlumineux arrive sur l'interface séparant l'air du coeur de la fibre au point d'incidence I.
Donner l'expression de l'angle ß en fonction de a, nair et nC.
Relation de Descartes pour la réfraction : nair sin a = nC sin ß ; sin ß = nair sin a / nC ; ß = arsin (nair sin a / nC)
Calculer ß. a = 17,0.
ß = arsin (1,00 sin 17 / 1,52) =11,1.
|
|
Le
rayon réfracté au point I se propage dans le coeur de la fibre jusqu'à
atteindre l'interface entre le coeur et la gaine, au point d'incidence
J.
Donner la relation entre les angles ß et i. Vérifier que i = 78,9°.
Les angles ß et i sont complémentaires ( triangle rectangle ) : ß + i = 90°.
i = 90 -ß = 90 -11,1 = 78,9°.
Les rayons lumineux se propagent dans la fibre optique par le phénomène de réflexion totale.
Rappeler pourquoi cette réflexion totale est nécessaire à la propagation correcte des rayons lumineux dans la fibre optique.
La
lumière transporte des informations codées en binaire ( le signal
électrique initial est converti en signal optique ). La transmission
est correcte si la lumière ne peut sortir qu'à l'extrémité de la fibre
optique. On doit observer le phénomène de réflexion totale pour tous
les points J.
Indiquer la condition sur l'angle i pour que le rayon lumineux subisse une réflexion totale en J.
En J, dans l'hypothèse d'une réfraction : ( on note r, l'angle réfracté )
nC sin i = nG sin r ; la valeur maximale de sin r est 1.
Dans ce cas limite : sin ilim =nG / nC= 1,48 / 1,52 = 0,974 ; ilim =76,8°.
En J, si l'angle d'incidencei est supérieur à 76,8 °, il y a réflexion totale.
La condition de réflexion totale en J est-elle remplie ? Justifier.
L'angle d'incidence i est égal à 78,9°, valeur supérieure à l'angle ilim. La condition de réflexion totale est remplie en J.
Pour
avoir le maximum de chance qu'un faisceau lumineux se propage dans une
telle fibre, faut-il essayer de le faire entrer dans la fibre avec des
angles d'incidence a plutôt faibles ou plutôt élévés ?
ß + i = 90°et i > ilim ; ß < 90 -ilim.
Or nC sin ß / nair= sin a ; a doit donc être petit.
|
Un
inconvénient de la fibre à saut d'indice est que des rayons
entrant simultanément dans la fibre avec des incidences différentes
parcourent des longueurs différentes et donc ressortent à l'autre
extrémité de la fibre à des instants différents. Ce phénomène limite le
nombre d'impulsions lumineuses que l'on veut faire passer par la fibre
chaque seconde, donc son débit. La fibre optique à gradient d'indice
permet d'avoir la même durée de parcours pour toutes les incidences a à l'entrée de la fibre.
Fibre optique à gradient d'indice.
L'indice
de réfraction varie progressivement du centre vers la surface
extérieure de la fibre. On peut modéliser la fibre par un assemblage de
strates concentriques d'indice de réfraction légérement différents :
Un
rayon lumineux se propage en ligne droite dans chaque strate, il subit
une réfraction à chaque changement de strate. Quand son incidence est
trop élevée, il subit une réflexion totale, ce qui lui permet de rester
dans la fibre, comme le montre la figure ci-dessous :
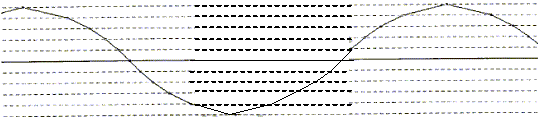
Indiquer
si l'indice de réfraction des différentes strates augmente ou diminue
du centre vers l'extérieur de la fibre. Argumenter la réponse.
Dans le cas de la fibre à saut d'indice, l'indice du coeur est supérieur à celui de la gaine.
Pour observer une réflexion totale, deux conditions doivent être remplies :
- l'indice du milieu 2 doit être inférieur à celui du milieu 1 ;
- l'angle d'incidence doit être supérieur à un angle d'incidence limite.
L'indice de réfraction des strates diminue donc du centre vers l'extérieur de la fibre.
Les
rayons d'un faisceau monochromatique entrant simultanément dans cette
fibre sous des incidences différentes n'ont pas la même trajectoire.

Que représente l'indice de réfraction d'un milieu transparent ?
Indice de réfraction = célérité de la lumière dans le vide divisée par la célérité de la lumière dans le milieu.
D'après
la figure ci-dessus, les rayons parcourent donc des distances
différentes dans la fibre mais ressortent pourtant quasiment
simultanément de la fibre optique.
Expliquer pourquoi.
La distance d est très inférieure à la longueur de la fibre optique.
|
|



