Réalisation d'une modulation d'amplitude : bac S Amérique du Nord 2011.

. . . .

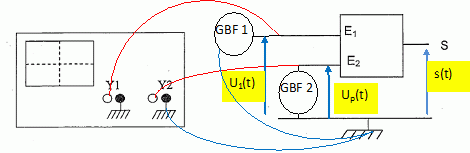
Des élèves de terminale S doivent mettre en oeuvre un montage permettant de simuler une modulation d'amplitude. Ils disposent du matériel suivant : - deux générateurs basse fréquence ( GBF) délivrant une tension sinusoïdale réglable en fréquence ; - un oscilloscope bicourbe : voies Y1 et Y2 ; - des fils de connexion ; - un circuit multiplieur, circuit intégré à deux entrées E1, E2 et une sortie S tel que : Us = k U1 U2 où k est une constante caractéristique du multiplieur. 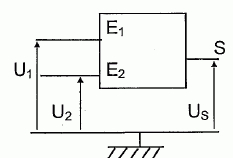Principe de la modulation d'amplitude. Pourquoi n'est-il pas possible de transmettre une onde sonore sur de grandes distances ? Une onde sonore est une onde mécanique  : celle-ci s'amortit assez rapidement ; de plus elle se propage dans l'air à une célérité voisine de 330 m/s. Enfin lors de la réception, il faut pouvoir sélectionner une station radio parmi beaucoup d'autres. Pour toutes ces raisons, on ne peut pas transmettre efficassement une onde sonore sur une grande distance. Pourquoi est-il  possible d'utiliser une porteuse de grande fréquence ? Une onde porteuse de grande fréquence est une onde électromagntique. L'amortissement est plus faible ; cette porteuse se propage dans l'air  à une célérité proche de 3 108 m/s. A la réception, on peut sélectionner une porteuse parmi beaucoup d'autres. Réalisation du montage. Compléter le schéma en y ajoutant les deux GBF et les flèches notées uP(t) pour la porteuse, u1(t) pour le signal modulant et s(t) pour le signal modulé. Représenter les fils de connexion à l'oscilloscope permettant de visualiser u1(t) sur la voie 1 et up(t) sur la voie 2. Etude de l'onde porteuse. Pour simuler l'onde porteuse, le GBF délivre une tension sinusoïdale up(t) d'amplitude UP=2,5 V et de fréquence fp=3000 Hz. L'oscilloscope est réglé pour visualiser sur la voie 1 avec une sensibilité horizontale de 0,1ms/ div et une sensibilité verticale de 1 V / div. Cette tension a pour expression : up(t) = UP cos ( 2pf t). Calculer la ériode TP de la porteuse. TP = 1/ fp = 1/3000 = 3,333 10-4 s = 0,3333 ms. Représenter cette tension. Etude du signal modulant. Pour simuler le signal modulant, le GBF délivre une tension u1(t) représentée ci-dessous : sensibilité verticale 0,5 V/div. 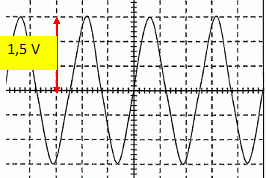Choisir en justifiant la réponse, l'expression de la tension u1(t) : u1(t) = U1 cos (2p f1 t) ou  u1(t) = U1 cos (2p f1 t) + U0. A l'instant t=0, d'après le graphe, u1(t=0) = 0 ; l'expression u1(t) = U1 cos (2p f1 t) + U0 est donc correcte avec U0 = -U1. Ajoutons qu'une bonne modulation d'amplitude correspond à U0 non nulle.   Choisir en justifiant la réponse, la fréquence f1 que doit délivrer le GBF : f1 = 10 000 Hz ; f1 = 100 Hz. La fréquence du signal modulant doit être très inférieure à la fréquence de la porteuse ( 3000 Hz ) : donc f1 = 100 Hz est correct.  De plus x" + k/ m x= ; on pose  w02 = k / m. Par suite 2p / T0 =(k / m)½ soit T0 = 2p (m / k)½. Déterminer l'amplitude U1 de la tension. Voir graphe ci-dessus Etude du signal modulé en amplitude. L'amplitude de la tension modulée, notée Um, varie entre deux valeurs extèmes, notée Umin et Umax. Faire apparaître Umin et Umax sur l'oscillogramme. Calculer le taux de modulation m =(Umax-Umin) / (Umax+Umin) m = (6,5-3,4) / (6,5 +3,4) =0,31. Quelle condition sur m permet d'éviter une surmodulation ? La surmodulation est évitée si le taux de modulation m est inférieur à 1. Les valeurs des fréquences utilisées précédemment ne correspondent pas à celles utilisées dans la réalité car elles nécessiteraient d'utiliser des antennes beaucoup trop grandes. Les ondes hertziennes kilométriques, appelées " grandes ondes " ont une longueur d'onde l comprise dans l'intervalle [1052 m ; 2000 m ]. Calculer l'ordre de grandeur de fréquence des ondes hertziennes. f = c / l = 3,0 108 / 1052 =2,8 105 Hz f = c / l = 3,0 108 / 2000 =1,5 105 Hz. Les fréquences des ondes hertziennes sont de l'ordre de 105 Hz.

menu